أتحقق من فهمي
ص: 49
أجد إحداثي النقطة (x,y) التي تجعل الاقتران: أكبر ما يمكن ضمن القيود الآتية:
التمثيل البياني لنظام المتباينات هو
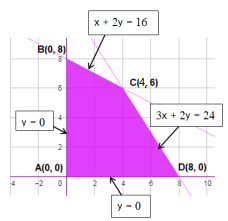
| رؤوس منطقة الحلول الممكنة | |
| A(0,0) | |
| B(0,8) | |
| C(4,6) | |
| D(8,0) |
النقطة التي يكون للاقتران أكبر قيمة عندها هي
أتحقق من فهمي
ص: 51
ينتج مشغل صغير للأثاث المعدني 36 خزانة على الأكثر في الأسبوع من نوعين مختلفين A، و B. وربحه في الخزانة الواحدة من النوع A هو 35 دينارا، ومن النوع B هو 45 دينارا. إذا كان ما يباع من النوع A لا يقل عن 3 أمثال ما يباع من النوع B، فأجد عدد الخزائن التي ينتجها المشغل من كل نوع ليحقق أكبر ربح ممكن.
أفرض أن عدد الخزائن التي ينتجها المشغل من النوع A هو x، ومن النوع B هو y
اقتران الهدف هو الربح المتوقع وهو:
القيود التي تحكم عمل المشغل هي:
يبين الشكل الىتي التمثيل البياني لنظام المتباينات الذي تكونه هذه القيود.
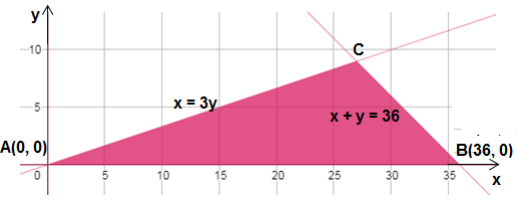
أجد إحداثي النقطة C بحل المعادلتين بالتعويض، فتكون
| رؤوس منطقة الحلول الممكنة | |
| A(0,0) | |
| B(36,0) | |
| C(27,9) |
يحقق المشغل أكبر ربح عندما ينتج 27 خزانة من النوع A، و9 خزائن من النوع B.
أتحقق من فهمي
ص: 53
رحلات: تخطط مدرسة ثانوية أن تأخذ ما لا يقل عن 400 طالب في رحلة لمدينة البترا. ولدى شركة نقل ركاب 10 حافلات كبيرة سعة الواحدة 50 راكباً، و 8 حافلات صغيرة سعة الواحدة 40 راكبا، ولديها 9 سائقين فقط. إذا كانت أجرة الحافلة الكبيرة 560 JD، والصغيرة 420 JD، فما أقل تكلفة ممكنة لاستئجار الحافلات لهذه الرحلة؟
أفرض أن عدد الحافلات الكبيرة المستأجرة لنقل الطلبة هو x، والصغيرة هو y تكلفة استئجار هذه الحافلات هي:
عدد ركاب هذه الحافلات 400 طالب على الأقل:
بالقسمة على 10 تصبح:
عدد السائقين 9:
عدد الحافلات الكبيرة لدى الشركة 10:
عدد الحافلات الصغيرة لدى الشركة 8:
يبين الرسم المجاور التمثيل البياني لنظام المتباينات السابقة:
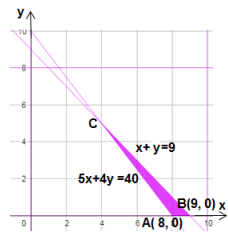
أجد إحداثيي C بحل المعادلتين فأجد أن إحداثيي C هما (4,5).
| رؤوس منطقة الحلول الممكنة | |
| A(8,0) | |
| B(9,0) | |
| C(4,5) |
إذن، أقل تكلفة لاستئجار الحافلات لهذه الرحلة هي 4340 دينار عند استئجار 4 حافلات كبيرة، و 6 صغيرة.
أتدرب وأحل المسائل
أجد إحداثي النقطة (x,y) التي تجعل اقتران الهدف أصغر ما يمكن ضمن القيود المعطاة في كل مما يأتي:
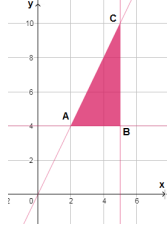
| رؤوس منطقة الحلول الممكنة | |
| A(2,4) | |
| B(5,4) | |
| C(5,10) |
أصغر قيمة لاقتران الهدف هي 18 عند النقطة A(2,4).
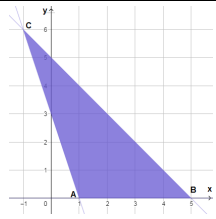
| رؤوس منطقة الحلول الممكنة | |
| A(1,0) | |
| B(5,0) | |
| C(-1,6) |
أصغر قيمة لاقتران الهدف هي 2 عند النقطة A(1,0).
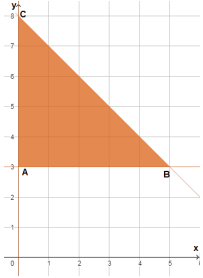
| رؤوس منطقة الحلول الممكنة | |
| A(0,3) | |
| B(5,3) | |
| C(0,8) |
أصغر قيمة لاقتران الهدف هي 6 عند النقطة A(0,3).
أجد إحداثي النقطة (x,y) التي تجعل اقتران الهدف أكبر ما يمكن ضمن القيود المعطاة في كل مما يأتي:
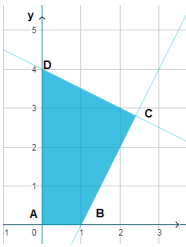
بعد تمثيل نظام المتباينات، أجد إحداثيي C بحل المعادلتين
فأجد أن إحداثيي C هما
| رؤوس منطقة الحلول الممكنة | |
| A(0,0) | |
| B(1,0) | |
| C(2.4,2.8) | |
| D(0,4) |
أكبر قيمة لاقتران الهدف هي 6.4 عند النقطة C(2.4,2.8)
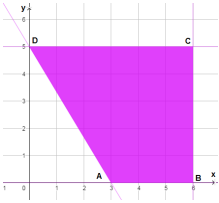
| رؤوس منطقة الحلول الممكنة | |
| A(3,0) | |
| B(6,0) | |
| C(6,5) | |
| D(0,5) |
أكبر قيمة لاقتران الهدف هي 23 عند النقطة C(6,5).
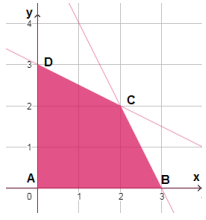
| رؤوس منطقة الحلول الممكنة | |
| A(0,0) | |
| B(3,0) | |
| C(2,2) | |
| D(0,3) |
أكبر قيمة لاقتران الهدف هي 6 وتتحقق عند النقطتين C(2,2),D(0,3)
لدى شركة لنقل الركاب حافلات كبيرة ومتوسطة، لا يزيد عددها الكلي على 15 ولا يقل على 8 حافلات. وكان عدد الحافلات المتوسطة لا يقل عن نصف عدد الحافلات الكبيرة، ولا يزيد على عدد الحافلات الكبيرة بأكثر من حا فلتين.
7) أكتب نظام متباينات يصف هذه المعلومات وأمثله بيانيا.
أفرض أن عدد الحافلات الكبيرة x، والمتوسطة y، فيكون نظام المتباينات هو:
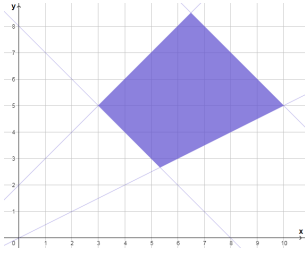
8) إذا كان لدى الشركة 6 حافلات كبيرة، فكم لديها من الحافلات الصغيرة؟ أكتب القيم الممكنة جميعها.
إذا كان لدى الشركة 6 حافلات كبيرة، فيمكن أن يكون لديها 3 أو 4 أو 5 أو 6 أو 7 أو 8 حافلات متوسطة.(نأخذ الإحداثيات y الصحيحة لجميع النقاط التي الإحداثي x لها 6 وتقع في منطقة الحلول الممكنة لنظام المتباينات).
9) إذا كانت أجرة رحلة بالقارب للواحدة من الكبار 20 JD، وللواحدة من الأطفال 10 JD. ويحمل القارب ما لا يزيد على 30 شخصا، ويجب ألا تقل الأجرة الكلية عن 480 JD فما أقل عدد ممكن للكبار الذين يحملهم القارب؟
أفرض أن عدد الكبار x، وعدد الأطفال y، فنظام المتباينات الذي يصف هذه المسألة هو:
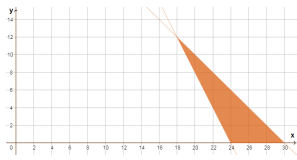
أقل عدد للكبار الذين يحملهم القارب هو أقل قيمة الإحداثي x للنقاط الواقعة في منطقة الحلول الممكنة وهو هنا 18
مكتبات عامة: يريد المسؤول عن مكتبة عامة شراء خزائن جديدة؛ تحتوي رفوفا مساحتها إذا كانت مساحة رفوف الخزانة الواحدة من النوع A هي ، ومن النوع B هي ، ويمكن أن تستوعب المكتبة 8 خزائن على الأكثر من النوع A، و 12 خزانة على الأكثر من النوع B.
10) إذا كان ثمن الخزانة من النوع A ، ومن النوع B ، فأكتب اقتران تكلفة شراء الخزائن ونظام متباينات يصف هذا الموقف.
أفرض أن عدد خزائن النوع A هو x، وعدد خزائن النوع B هو y
تكلفة شراء هذه الخزائن هي:
نظام المتباينات الذي يصف هذا الموقف هو:
.
11) أمثل منطقة حل نظام المتباينات، وأجد إحداثيات رؤوسها.
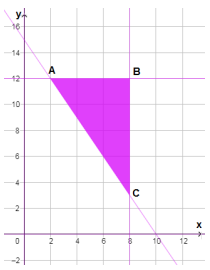
رؤوس منطقة الحل هي:
12) أجد عدد الخزائن من كل نوع التي يجب أن يشتريها المسؤول عن المكتبة، لتحقيق حاجته من الخزائن بأقل تكلفة ممكنة.
أحسب قيمة اقتران التكلفة عند رؤوس منطقة الحلول الممكنة.
| رؤوس منطقة الحلول الممكنة | |
| A(2,12) | |
| B(8,12) | |
| C(8,3) |
أقل تكلفة ممكنة هي 945 دينارا عند شراء 8 خزائن من النوع A، و3 خزائن من النوع B.
13) ينتج مصنع نوعين من الدراجات الهوائية، وتبلغ طاقته الإنتاجية القصوى من كلا النوعين 420 دراجة أسبوعيا. فإذا كان عليه أن ينتج ما لا يقل 100 دراجة من النوع الاول، وما لا يزيد على 200 دراجة من النوع الثاني في أحد الاسابيع، وكان ثمن بيع الدراجة من النوع الأول 60 JD، ومن النوع الثاني 75 JD، فكم دراجة ينتج من كل نوع ليكون دخل المصنع أكبر ما يمكن في ذلك الأسبوع؟
أفرض أن عدد الدراجات التي ينتجها المصنع أسبوعيا من النوع الأول x، ومن النوع الثاني y
نظام المتباينات الذي يصف المسألة هو:
اقتران الهدف هو دخل المصنع من بيع الدراجات وهو:
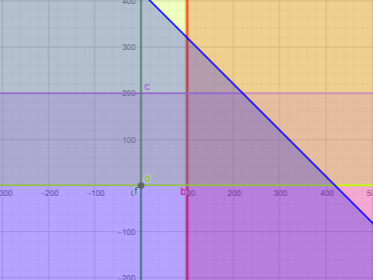
يكون الدخل أكبر ما يمكن عند انتاج 220 دراجة من النوع الأول، و200 دراجة من النوع الثاني.
زراعة: يباع في محل للوازم الزراعية نوعان من الأسمدة هما A,B، ويبن الجدول المجاور مكونات الكيلو غرام الواحدة من هذين السمادين:
| النوع |
فوسفات (وحدة) |
نيترات (وحدة) |
أمونيا (وحدة) |
| A | 6 | 3 | 3 |
| B | 4 | 4 | 10 |
يريد مزارع أن يكون مزيجا من السمادين يحتوي على 36 وحدة على الأقل فوسفات، و24 وحدة على الأقل نيترات، و30 وحدة على الأقل أمونيا.
14) إذا كان ثمن الكيلوجرام من النوع A دينارا واحدا، ومن النوع B ، فأكتب اقتران التكلفة ونظام متباينات يصف هذا الموقف.
أفرض أن المزارع يشتري x KG من النوع A، و y KG من النوع B
اقتران التكلفة هو:
نظام المتباينات الذي يصف هذه المسألة هو:
كمية الفوسفات:
كمية النيترات:
كمية الأمونيا:
عدم السالبية:
15) أمثل منطقة حل نظام المتباينات، وأجد إحداثيات رؤوسها.
أجد إحداثيي C بحل المعادلتين
فأجد أن
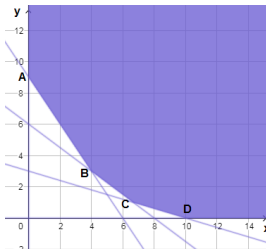
رؤوس منطقة الحلول الممكنة هي:
16) أجد عدد الكيلوغرامات التي يشتريها من كل نوع؛ ليحقق غايته بأقل تكلفة.
أحسب قيمة اقتران التكلفة عند رؤوس منطقة الحلول.
| رؤوس منطقة الحلول الممكنة | |
| A(0,9) | |
| B(4,3) | |
| D(10,0) |
أقل تكلفة هي 7.16 JD عند شراء من السماد A، و 1KG من السماد B.
مهارات التفكير العليا
17) تبرير: أجد أكبر قيمة ممكنة لاقتران الهدف ضمن منطقة الحلول الممكنة الممثلة في الشكل المجاور وأبرر إجابتي، ثم أجد نقاطا أخرى ضمن منطقة الحل يتحقق عندها أكبر قيمة لا قتران الهدف، وأبرر إجابتي.
أحسب قيمة الاقتران الهدف عند رؤوس منطقة الحلول الممكنة.
| رؤوس منطقة الحلول الممكنة | |
| (0,0) | |
| (0,45) | |
| (30,45) | |
| (60,20) | |
| (60,0) |
أكبر قيمة لاقتران الهدف هي 420 وتتحقق عند الرأسين ، وذلك لأن المستقيم الحدودي المار بهاتين النقطتين يوازي المستقيم الذي يمثل اقتران الهدف فميلاهما متساويان وجميع النقاط الواقعة على هذا الحد تعطي القيمة نفسها لاقتران الهدف ومنها وغيرها، لأن معادلة هذا الحد هي .
18) مسألة مفتوحة: أكتب مسألة حياتية يمكنني حلها باستعمال البرمجة الخطية تحتوي 4 متباينات على الأقل، ثم أكتب اقتران الهدف وأجد قيمته العظمى والصغرى.
تتنوع الإجابات. المسألة الآتية مثال لإجابة:
ينتج مصنع أثاث طاولات وخزائن. يتطلب صنع الطاولة الواحدة ساعتان من العمل الآلي وساعة عمل يدوي، بينما يتطلب صنع الخزانة الواحدة ساعة عمل آلي وساعتا عمل يدوي.
ويمكن أن تعمل الآلات في المصنع في المصنع مدة 180 ساعة أسبوعيا، ويمكن تنفيذ 270 ساعة عمل يدوي أسبوعيا. إذا كان المصنع يربح 5 دنانير في كل طاولة، و8 دنانير في كل خزانة، فكم طاولة وخزانة ينتج المصنع أسبوعيا ليحقق أكبر ربح؟
أفرض أن عدد الطاولات x، والخزائن y.
نظام المتباينات الذي يصف هذه المسألة هو:
عدد ساعات العمل الآلي المتاحة:
عدد ساعات العمل اليدوي المتاحة:
عدم السالبية:
أحل المعادلتين
فأجد أن إحداثيي C هما (30,120)
لإيجاد إحداثي B أعوض y=0 في المعادلة 2x+y=180
فينتج أن: x=90
لإيجاد إحداثيي B أعوض x=0 في المعادلة x+2y=270
فينتج أن y=135
اقتران الهدف هو الربح P=5x+8y
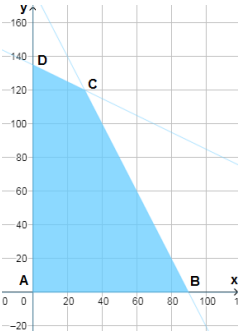
أحسب قيمة اقتران الهدف عند رؤوس منطقة الحل
| رؤوس منطقة الحلول الممكنة | |
| A(0,0) | |
| B(90,0) | |
| C(30,120) | |
| D(0,135) |
يحقق المصنع أكبر ربح أسبوعي قدره 870 دينارا عندما ينتج 30 طاولة، و 120 خزانة.
19) تبرير: هل يكون لاقتران الهدف قيمة عظمى موجبة؛ إذا وقعت منطقة حل النظام المتباينات المرتبطة به في الربع الأول؟ أبررإجابتي.
قد تكون موجبة وقد تكون غير ذلك لأن الأمر يعتمد على المعاميلن a، وb بالإضافة إلى قيمة x، وy.
20) تحد: أجد القيمة العظمى والقيمة الصغرى للاقتران ضمن القيود المعطاة في ما يأتي:
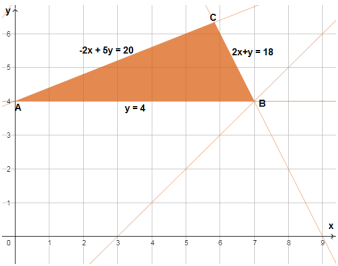
أجد إحداثيي C بحل المعادلتين فأجد أن
ثم أحسب قيمة اقتران الهدف عند رؤوس منطقة الحلول الممكنة.
| رؤوس منطقة الحلول الممكنة | |
| A(0,4) | |
| B(7,4) | |
| C(4.5,6.75) |
القيمة العظمى هي 20.25، والقيمة الصغرى 1-.
حل أسئلة كتاب التمارين
أجد إحداثي النقطة (x,y) التي تجعل اقتران الهدف أصغر ما يمكن؛ ضمن القيود المعطاة في كل مما يأتي:
| T = 3x + y | رؤوس منطقة الحلول الممكنة |
| A(-2,4) | |
| B(5,4) | |
| C(5,-3) |
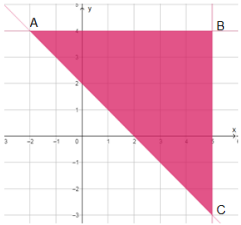
أصغر فيمة لاقتران الهدف هي 2- عند النقطة
| رؤوس منطقة الحلول الممكنة | P = 5x + 2y |
| A(0,1) | |
| B(1,3) | |
| C(4,0) |
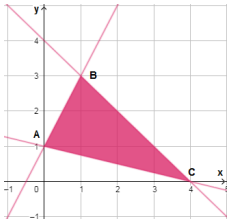
أصغر قيمة لاقتران الهدف 2 عند النقطة A(0,1)
| R=10x-3y | رؤوس منطقة الحلول الممكنة |
| A(-4,4) | |
| B(3,5) | |
| C(2,-8) |
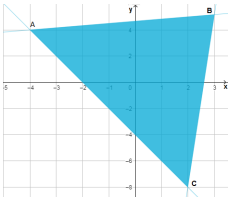
إحداثيات النقطة B هما تقريبا (3,5).
أصغر قيمة لاقتران الهدف هي 52- عند النقطة A(-4,4)
أجد إحداثيي النقطة (x,y) التي تجعل اقتران الهدف أكبر ما يمكن؛ ضمن القيود المعطاة فيكل مما يأتي:
| S = 2x + 14 | رؤوس منطقة الحلول الممكنة |
| A(2,-4) | |
| B(4,-4) |
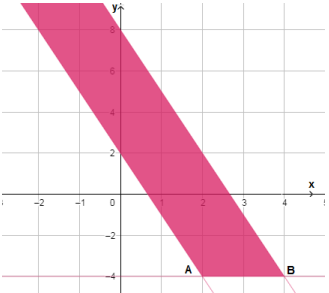
لا يوجد لهذا الاقتران قيمة عظمى لأنه أكبرمن 48-، فمثلا عند النقطة الواقعة في منطقة الحل تكون قيمته 108 ويأخذ قيما أكبر من ذلك عند نقاط أخرى في منطقة الحل.
| W=-3x-6y | رؤوس منطقة الحلول الممكنة |
| A(-2,6) | |
| B(-8,-2) | |
| C(2,-2) |
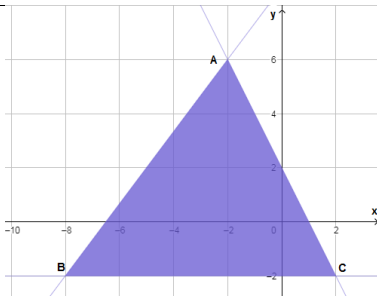
أكبر قيمة لاقتران الهدف هي 36 عند النقطة
| M =6x + 7y | رؤوس منطقة الحلول الممكنة |
| A(2,5) | |
| B(2,0) | |
| C(6,-1) | |
| D(6,3) |
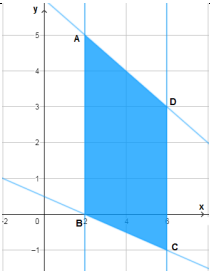
أكبر فقيمة لاقتران الهدف هي 57 وتحقق عند النقطة D(6,3)
آلات حاسبة: تصنع شركة نوعين من آلالات الحاسبة: عادية، وعلمية. ويتطلب السوق أن تصنع الشركة على الأقل 100 آالة عادية، و800 آلة علمية يوميا؛ لكن طاقة الشركة الأنتاجية تحتم ألا يزيد عدد آلالات الحاسبة العادية على 200 آلة، وألا يزيد عدد آلالات الحاسبة العلمية على 170 آلة يوميا. ولوفاء الشركة بعقودها؛ يجب أن تصنع ما لا يقل عن 200 آلة حاسبة من النوعين معا يوميا.
7) إذا كانت تكلفة إنتاج الآلة الحاسبة العادية الواحدة 3.5 JD، وتكلفة الآلة الحاسبة العلمية الواحدة 5 JD، فكم آلة تصنع من كل نوع يوميا؛ لتجعل التكلفة أقل ما يمكن؟
أفرض أن عدد الآلات العادية التي تصنعها الشركة هو x، وأن عدد الآلات العلمية هو y.
اقتران التكلفة هو: C=3.5x+5y، ضمن القيود الآتية:
| رؤوس منطقة الحلول الممكنة | C =3.5x + 5y |
| A(100,170) | |
| B(200,170) | |
| C(200,80) | |
| D(120,80) | |
| E(100,100) |
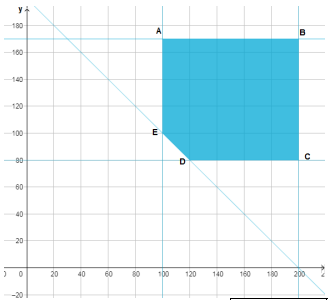
تكون تكلفة أقل ما يمكن عندما تصنع الشركة 120 آلة حاسبة عادية، و80 آلة حاسبة علمية يوميا.
8) إذا كانت الشركة تربح 0.5 JD في الآلة الحاسبة العادية و 3 JD في الآلة الحاسبة العلمية، فكم آلة تصنع من كل نوع يوميا لتحقق أكبر ربح؟
| P =0.5x + 3y | رؤوس منطقة الحلول الممكنة |
| A(100,170) | |
| B(200,170) | |
| C(200,80) | |
| D(120,80) | |
| E(100,100) |
تحقق ىالشركة أكبر ربح يومي قدره 610 دنانير عندما تنتج 200 آلة عادية، و 170 آلة علمية يوميا.
9) عقارات: لدى شركة عقارية 100 قطعة أرض، وكانت تخطط لبناء نوعين من البيوت على هذه القطع. يكلف بناء البيت من النوع الأول 30000 دينار ويعود عليها بربح مقداره 4300 دينار عند بيعه، ويكلف بناء البيت من النوع الثاني 45000 دينار ويعود بربح مقداره 6400 دينار عند بيعه. إذا كلن مع هذا المستثمر مبلغ 3.6 مليون دينار، فكم بيتا يبني من كل نوع ليحقق أكبر ربح؟

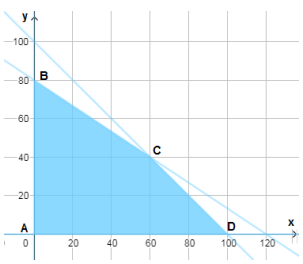
تحقق الشركة أكبر ربح وقدره 514000 دينار عندما تبني 60 بيتا من النوع الأول، و40 بيتا من النوع الثاني.