رياضيات فصل أول

التحويلات الهندسية للاقترانات

الاقترانات الرئيسية

عائلة الاقترانات: هي مجموعة الاقترانات التي تتشابه منحنياتها في صفة واحدة أو أكثر ويسمى أبسط هذه الاقترانات الاقتران الرئيس.

مثال:

الاقتران الرئيس لعائلة الاقترانات الخطية هو f(x)=x ويسمى الاقتران المحايد ومن عائلته f(x)=x-1, g(x)=3x, j(x)=1-2x ومن الاقترانات الرئيسية الأكثر شيوعا.

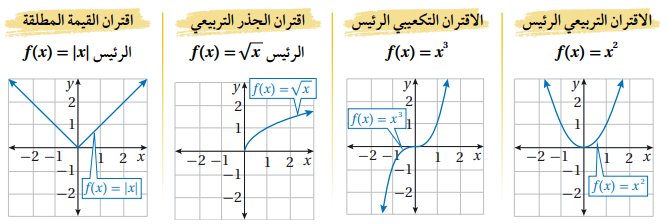
ملاحظة: إذا عرف شكل منحنى الاقتران الرئيس هذا يساعد على تمثيل منحنيات أكثر تعقيدا من نفس العائلة والتي تكون ناتجة عن تطبيق تحويل هندسي أو أكثر على منحنى الاقتران الرئيس حيث يكون التغيير في موقع المنحنى دون تغيير شكله وأبعاده كلإنعكاس والانسحاب أما تحويلات التمدد فتغيير شكل المنحنى بحيث يبدو أوسع أو أضيق من المنحنى الرئيس.

الانسحاب الرأسي:

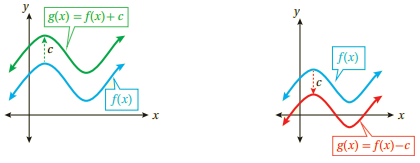
نقل منحنى الاقتران إلى الأعلى عند إضافة ثابت موجب للاقتران وإلى الأسفل عند طرح ثابت موجب من الاقتران.

إذا كان f اقتران وكان c عددا حقيقيا موجبا؛ فإن: منحنى g(x)=f(x)+c وهو منحنى f(x) مزاحا إلى الأعلى c وحدة. منحنى g(x)=f(x)-c هو منحنى f(x) مزاحا إلى الأسفل c وحدة.

 

الانسحاب الأفقي:

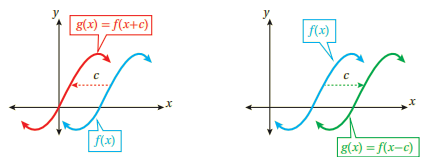
هو تحويل هندسي ينقل منحنى الاقتران إلى اليسار عند إضافة ثابت موجب إلى قيم x وإلى اليمين عند طرح ثابت موجب من قيم x.

إذا كان f اقترانا وكان c عددا حقيقيا موجبا؛ فإن: منحنى g(x)=f(x+c) هو منحنى f(x) مزاحا إلى اليسار c وحدة. منحنى g(x)=f(x-c) هو منحنى f(x) مزاحا إلى اليمين c وحدة.

 

الانعكاس:

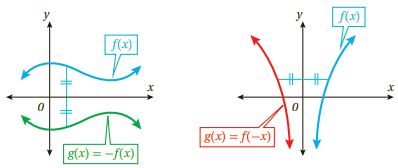
هو تحويل هندسي يعكسئ منحنى الاقتران حول مستقيم محدد.

منحنى g(x)=-f(x) هو انعكاس لمنحنى f(x) حول المحور x. منحنى g(x)=f(-x) هو انعكاس لمنحنى f(x) حول المحور y.

 

التمدد الرأسي:

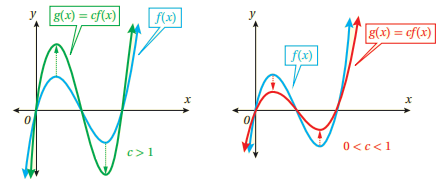
هو تحويل هندسي يؤدي إلى توسيع منحنى الاقتران أو تضييقه رأسيا.

إذا كان c عددا حقيقيا موجبا، فإن منحنى g(x)=cf(x) هو: توسيع رأسي بمعامل مقداره c لمنحنى f(x)، إذا كانت c>1 تضييق رأسي بمعامل مقداره c لمنحنى f(x)، إذا كانت $0<c<1$

 

التمدد الأفقي:

هو تحويل هندسي يؤدي إلى توسيع منحنى الاقتران أو تضييقه أفقيا.

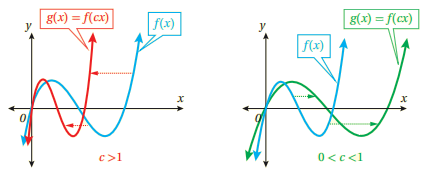
إذا كان c عددا حقيقيا موجبا؛ فإن منحنى g(x)=f(cx) هو: تضييق أفقي لمنحى f(x)، إذا كانت c>1 بمعامل مقداره $\frac{1}{c}$. توسيع أفقي لمنحنى f(x)، إذا كانت $0<c<1$ بمعامل مقداره $\frac{1}{c}$.

 

 

 

سلسلة التحويلات الهندسية:

ويكون ذلك عند تطبيق أكثر من تحويل هندسي على الاقتران الرئيس وتكون على الترتيب الآتي: