الفيزياء 11 فصل ثاني

الحركة الموجية:

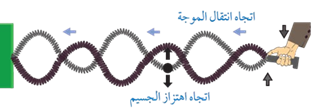
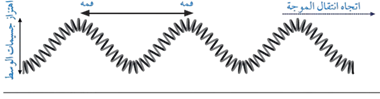
تُعدّ الحركة الموجية من الظواهر الطبيعية التي نشاهدها كثيرًا في الحياة. ويبيّن الشكل إحدى أبسط الطرق لتوليد الموجات؛ وذلك بتثبيت نابض من أحد طرفيه، وتحريك طرفه الآخر إلى الأعلى وإلى الأسفل.

فإذا كان طرف النابض متصلً بمولّد ذبذبات يهتزّ بانتظام بحركة توافقية بسيطة، فسيتولّد في النابض موجات دورية تتكرّر بانتظام.

---

عند مراقبة نقطة مفردة (جسيم) على النابض، نلاحظ أنه عند انتقال نبضة موجية من اليمين إلى اليسار فإن الجسيم يهتزّ إلى الأعلى وإلى الأسفل حول موقع اتزانه، كما يبيّن الشكل، ونظرًا إلى أن مصدر الموجات يهتزّ بحركة توافقية بسيطة، فإن اهتزاز الجسيم يكون بحركة توافقية بسيطة أيضًا.

 

 

 

ويتضح من الشكل أن الموجة - في هذه الحالة - يمكن تمثيلها بيانيًّا باقتران الجيب؛ لذا تُسمّى موجة جيبية.

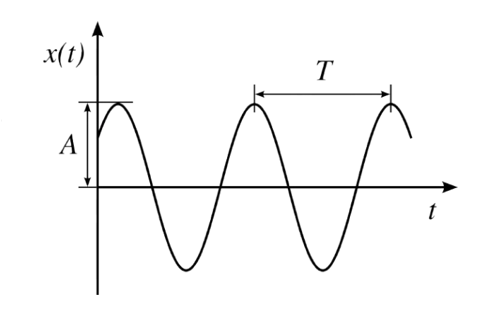
يمكن تمثيل التغير في الإزاحة الرأسية لجسيم من جسيمات الوسط مع الزمن بيانيًّا كما يبيّن الشكل إذ يصف المنحنى كيف يتغيّر موقع هذا الجُسيم مع مرور الزمن.

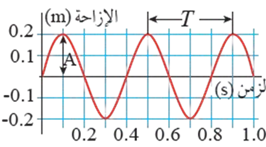
فالجسيم الواحد يصل إلى أقصى موقع رأسي له عن موقع الاتزان، ثمّ ينخفض إلى أسفل موقع، ثم يعود إلى موقع اتّزانه خلال دورة واحدة.

توصف الحركة الموجية باستخدام المفاهيم نفسها المستخدمة لوصف الحركة التوافقية البسيطة، حيث تُعرَّف سَعة الموجة (A) أنها أقصى إزاحة رأسية للجسيم عن موقع الاتزان.

أما الزمن الدوري للموجة (T) فهو الزمن اللازم لمرور موجة كاملة خلال نقطة محددة، ويتناسب الزمن الدوري للموجة عكسيًّا مع تردّدها (f) حسب العلاقة:

$T=\frac{1}{f}$

---

الموجات الميكانيكية

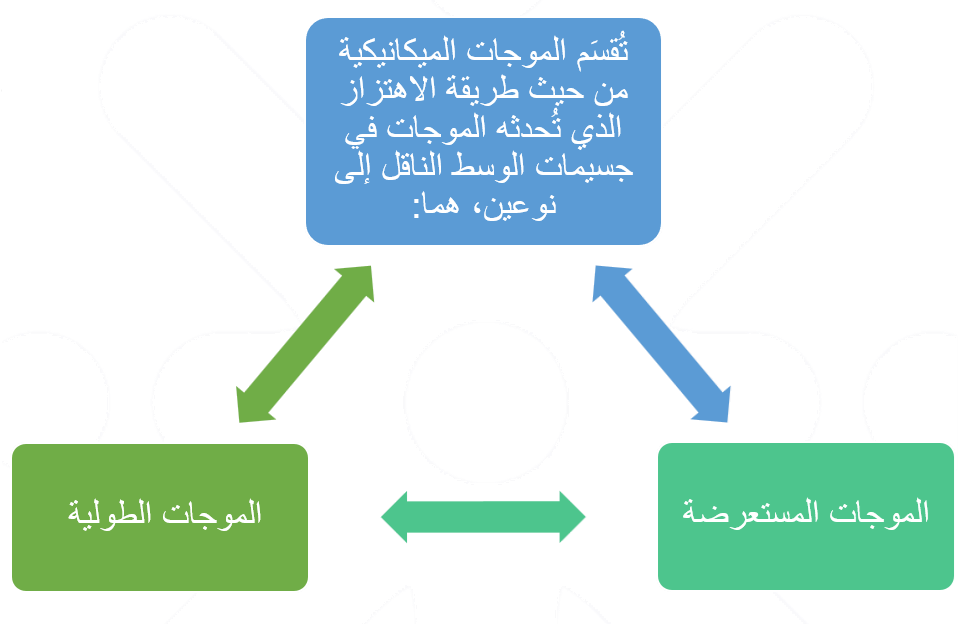
تُصنَّف الموجات المنتقلة عبر النابض بأنها موجات ميكانيكية، وهي موجات تحتاج إلى وسط مادي تنتقل خلاله.

 

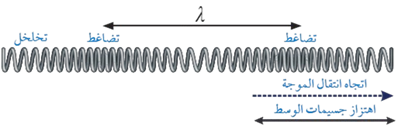
من المفاهيم المهمة المستخدمة لوصف الحركة الموجية: الطول الموجي ويُرمَز إليه بالرمز (λ )، ويبيّن الشكل أن الطول الموجي للموجة المستعرضة هو المسافة بين قمّتين متتاليتين، أو المسافة بين قاعين متتاليين.

أمّا الطول الموجي للموجة الطولية فهو المسافة بين مركزَي تضاغطين متتاليين أو تخلخلين متتاليين، كما يبيّن الشكل.

---

أتحقّق: أوضح المقصود بكل من التردّد والزمن الدوري، ثم أصف العلاقة بينهما.

الحل:

• التردد: هو عدد الذبذبات أو الدورات الكاملة التي تحدث في وحدة الزمن. يُقاس التردد بوحدة الهرتز (Hz)، حيث أن:1 هرتز = 1 دورة في الثانية.
• الزمن الدوري: هو الزمن اللازم لعمل ذبذبة واحدة كاملة، أي أنه الزمن الذي تستغرقه الموجة لإكمال دورة واحدة. يُقاس الزمن الدوري بوحدة الثانية  (s).

سرعة الموجة في الوسط الواحد فهي ثابتة، ويعتمد مقدارها على نوع الوسط وصفاته، وترتبط سرعة الموجة (ورمزها(.(v)  بكلّ من التردّد والطول الموجي بالعلاقة الرياضية الآتية:

$v = f \lambda$

---

تداخل الموجات

تعرفت ظاهرة تميّز الموجات عن الجسيمات المادية تُسمّى التداخل.

 

 

 

تحدث ظاهرة التداخل عند التقاء موجتين أو أكثر عند النقطة نفسها، وفي اللحظة التي تلتقي فيها الموجتان تتشكّل موجة محصلة، وتكون الإزاحة الكلية عند أي نقطة مساوية لناتج جمع الإزاحتين الناتجتين من الموجتين، وتُعرَف هذه الطريقة في جمع الإزاحات الناتجة من التقاء موجتين أو أكثر بمبدأ التراكب .

وبعدَ التراكبِ تستعيد كلّ من الموجتين المتراكبتين شكلها الأصلي الذي كانت عليه. ويبيّن الشكل مثالً على تداخل نبضتين )موجتين( تنتقلان عبر حبل، وتتحركان نحو بعضهما. وبدراسة الشكل أتوصّل إلى الأمور الآتية:

 

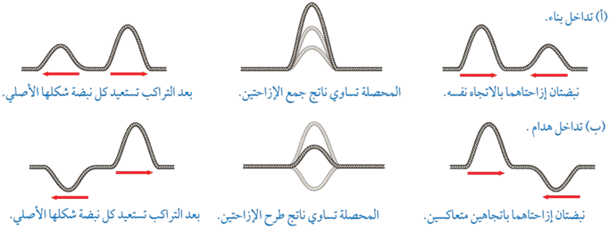
عند التقاء موجتين إزاحتاهما بالاتجاه نفسه، فإن المحصلة تساوي ناتج جمع إزاحتيهما، وتكون السعة الناتجة أكبر من السعة لكل منهما، كما يبيّن الشكل ) أ(.

يُسمّى نمط التراكب هذا التداخل البنّاء.

عند التقاء موجتين إزاحتاهما متعاكستان، مثلً: قمة موجة مع قاع موجة، فإن المحصلة تساوي ناتج طرح الإزاحتين وتكون باتجاه الإزاحة الأكبر، كما يبيّن الشكل )ب(.

يُسمّى نمط التراكب هذا التداخل الهدّام

---

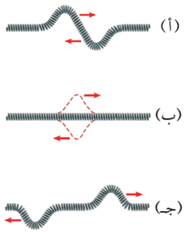
أتحقّق: نبضتان موجيّتان متساويتان في السعة تنتقلان في نابض، كما هو مُبيَّن في الشكل أصف ما يحدث لحظة التقاء النبضتين وبعد التقائهما.

الحل:

لحظة التقاء النبضتين يحدث بينهما تراكب (تداخل) هدام، وحيث أنهما متساويتان في السعة يكون تداخلاً هداماً تاما، فتختفي النبضتان، وبعد أن تتعدى كل. منهما الأخرى تعودان للظهور كما كانتا قبل التراكب.

---

التداخل وفرق الطور

ذكرنا سابقًا أن زاوية الطور (∅) تحدّد موقع الجسم المهتزّ لحظة بداية الحركة.

 

 

 

وعند تطبيق مبدأ التراكب على موجتين جيبيتين متساويتين في السعة والتردد والطول الموجي، فإن نمط التداخل الناتج من تراكب الموجتين يعتمد على مقدار الفرق في الطور بين الموجتين بالنسبة إلى بعضهما؛ أي يعتمد على مقدار فرق الإزاحة الذي تتقدّم فيه إحدى الموجتين عن الأخرى.

ويبيّن الشكل نمطَي تداخل خاصَّين لموجتين جيبيتين متساويتين في السعة والتردد والطول الموجي وتتحرّكان بالاتجاه نفسه، عبر وتر مشدود.

 

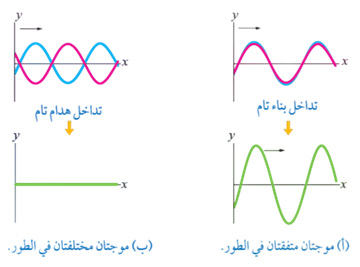
الشكل (أ) القمم والقيعان للموجة الأولى متطابقة تمامًا مع القمم والقيعان للموجة الثانية، فيكون فرق الطور بينهما صفرًا ($\varnothing =0°$)، وتوصف الموجتان بأنهما متفقتان في الطور .

وتكون سعة الموجة الناتجة من التداخل البنّاء للموجتين ضعف سعة أيّ من الموجتين، ويُسمّى التداخل في هذه الحالة تداخلً بنّاءً تامًّا.

الشكل (ب) القمم للموجة الأولى متطابقة مع القيعان للموجة الثانية، فيكون فرق الطور بينهما يساوي $\varnothing =\pi rad$أو $180°$ ، وتوصف الموجتان بأنهما مختلفتان في الطور ، وتكون الإزاحة المحصلة صفرًا؛ أي تلغي الموجتان بعضهما، ويُسمّى التداخل في هذه الحالة تداخلً هدّامًا تامًّا.

 

---

أتحقّق: موجتان متساويتان في السعة والتردد والطول الموجي، وتتحركان بالاتجاه نفسه عبر نابض. ما الشرط اللازم للحصول على نمط:

- تداخل بنّاء تام.

- تداخل هدّام تام.

الحل:

للحصول على نمط تداخل بنّاء تام يجب أن تكون الموجتان متساويتان في الطور (لا يوجد بينهما فرق في الطور ).

للحصول على نمط تداخل هدّام يجب أن يكون بينهما فرق في الطور يساوي (

 

 

π) وهذا ما يعادل نصف طول موجي .

---

الموجات الموقوفة في الأعمدة والأوتار

يبيّن الشكل )أ( خمسة مشاهد متتالية لموجتين جيبيتين؛ الأولى تنتقل عبر وتر مشدود من اليمين إلى اليسار، والثانية تنتقل عبر الوتر نفسه من اليسار إلى اليمين، ويبيّن الشكل (ب) المحصلة الناتجة من تراكب الموجتين.

 

ألاحظ أن نمط التداخل يتميز بوجود مواقع على طول الوتر تنعدم عندها الإزاحة تُسمّى عقدًا.

وفي منتصف المسافة بين العقد المتجاورة توجد مواقع يكون للإزاحة عندها قيم عظمى تُسمى بطونًا.

 

ويُسمّى نمط التداخل في هذه الحالة الموجة الموقوفة؛ لأن الموجة الناتجة تبدو كأنها ثابتة على الوتر، ومواقع البطون والعقد لا تتغيّر أيضًا.

تنتج الموجات الموقوفة من تراكب موجتين ضمن شروط محدّدة، إذ تعرف الموجات الموقوفة بأنها أنماط موجية ثابتة الأشكال تنتج من تراكب موجتين متساويتين في التردّد والطول الموجي والسعة، تنتقلان في اتّجاهين متعاكسين في الوسط نفسه.

وهي ظاهرة تحدث في الموجات المستعرضة والموجات الطولية، وسنتناول مثالً على الموجات المستعرضة الموقوفة وهي موجات الوتر، ومثالً على الموجات الطولية الموقوفة وهي موجات الأعمدة الهوائية.

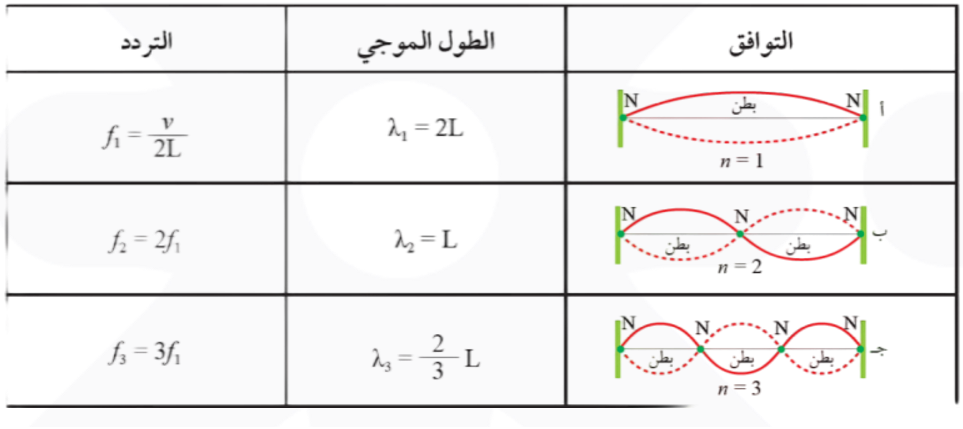
بدراسة الأنماط المبينة في الشكل ، ألاحظ أن طرفي الوتر يجب أن يكونا عقدتين، وأن البعد بين كل عقدتين متتاليتين يكافئ نصف الطول الموجي.

هذا يعني أن الترددات المناسبة للحصول على موجات موقوفة هي الترددات التي تحقق هذين الشرطين.

 

يتضح من الشكل أيضًا أن النمط الأول يتكون من بطن وعقدتين، ويحدث هذا النمط عندما يكون طول الوتر مساويًا لنصف الطول الموجي.

أما النمط الثاني فيتكون من بطنين وثلاث عقد، أي أن الطول الموجي للموجة المتكونة في النمط الثاني يساوي طول الوتر.... وهكذا لبقية الأنماط.

يمكن التوصل تجريبيًّا إلى علاقة رياضية لحساب الترددات اللازمة لإحداث موجات موقوفة على وتر بإجراء التجربة الآتية.

توصلت في التجربة السابقة إلى الترددات المناسبة للحصول على موجات موقوفة في وتر شدود. ولاحظت وجود تردد أدنى للمصدر الموّلد للموجات الموقوفة؛ وهو التردد اللازم للحصول على النمط الأول المكوّن من عقدتين وبطن واحد ويسمى التوافق الأول. وبما أن طول الوتر L))  في هذه الحالة يكون مساويًا لنصف الطول الموجي (${\lambda }_1$) فإن:

${\lambda }_1=2L$

وباستخدام العلاقة ($v=\lambda f$)؛ حيث $\left(v\right)$ سرعة الموجات، فإن تردد التوافق الأول يعطى بالعلاقة:

$f=\frac{v}{\lambda }=\frac{v}{2L}$

حيث (f₁) التردد الأساسي للموجات الموقوفة المتكونة في الوتر،أي أن ترددات الموجات الموقوفة هي من مضاعفات (f₁) وتسمى التوافقات، حيث يمكن حساب تردد التوافق ذو الرقم (n) باستخدام العلاقة:

$f_n=n\frac{v}{2L}=n{f}_1$

 

ويبين الجدول (1) ملخصًا للطول الموجي والتردد لأنماط الموجات الموقوفة في وتر.

الموجات الموقوفة في الأعمدة الهوائية:

يُحدِث عازف البوق الذي يظهر في الشكل اهتزازات عند طرف البوق، تنتقل خلال عمود الهواء إلى داخل البوق على شكل موجات صوتية، وتنعكس عن الطرف الثاني للبوق، سواء أكان مغلقًا أم مفتوحًا، فيحدث تداخل بين الموجات الصادرة والموجات المنعكسة، وتنشأ موجات طولية موقوفة في عمود الهواء، كتلك المستعرضة التي تحدث في وتر مشدود.

يُغيّر العازف التردّد بتغيير طول عمود الهواء، عندما يفتح الصمام بضغط الأصبع؛ فتتغيّر النغمة.

 

الأعمدة الهوائية المفتوحة

نقصد بعمود الهواء المفتوح أن يكون مفتوح البداية ومفتوح النهاية.

تتكوّن الموجات الموقوفة في الأعمدة الهوائية المفتوحة على أنْ تكون سَعة الاهتزاز عظمى عند نهايتَي الأنبوب، وتظهر في الشكل على هيئة بطون.

تنشأ الموجات الموقوفة بتردّدات مختلفة بما يُحقّق مجموعة من التوافقات، فنحصل على التوافق الأول والثاني والثالث، وغيرها، كما في حالة الوتر تمامًا.

 

يُحسب الطول الموجي للموجات الصوتية الموقوفة للتوافق. ($n$)

في عمود الهواء المفتوح النهاية وفقًا للعلاقة المستخدمة في الموجات المستعرضة. $n{\lambda }_n=2L$

 

وكذلك التردّد للتوافق رقم () يساوي:

$f_n=\frac{v}{{\lambda }_n}=\frac{nv}{2L}=n{f}_1$

حيثُ $\frac{v}{2L}=f_1$ تردد التوافق الأول

---

الأعمدة الهوائية المغلقة

نقصد بعمود الهواء المغلق أن يكون مفتوح البداية ومغلق النهاية. تتكوّن الموجات الموقوفة في الأعمدة الهوائية المغلقة النهاية، على أنْ تكون سعة الاهتزاز صفرًا عند النهاية المغلقة للأنبوب، وتظهر في الشكل على هيئة عُقد.

وتختلف التوافقات الناتجة هنا عمّا سبق، إذ تتكوّن التوافقات الفردية فقط، وذلك كي يتحقّق تكوّن العُقد عند النهاية المغلقة للأنبوب.

 

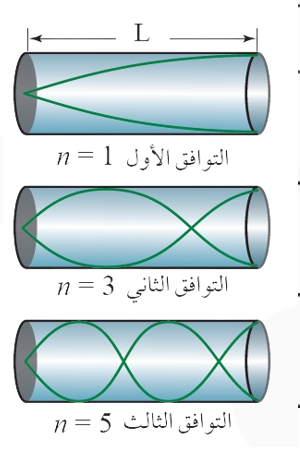
ويُحسب الطول الموجي للتوافق (n)، حيث (n) عدد صحيح فردي، وفقًا للعلاقة:

$n{\lambda }_n=2L$

وكذلك التردّد للتوافق رقم (n) يساوي:

$f_n=\frac{v}{{\lambda }_n}=\frac{nv}{2L}=n{f}_1$