|
التصادمات للتصادمات نوعان رئيسان؛ مرن وغير مرن. وتساعد معرفتهما على تصميم الأجهزة والأدوات المتعددة التي يعتمد مبدأ عملها على هذه التصادمات أو الحماية منها. |
|
 |
 |
|
الزخم الخطي والطاقة الحركية في التصادمات Linear Momentum and Kinetic Energy in Collisions يستخدم مصطلح تصادم لتمثيل حدث يقترب فيه جسمان أحدهما من الآخر، ويؤثر كل منهما في الآخر بقوة. وقد يتضمن التصادم تلامسا بين جسمين؛ مثل التصادم بين كرتين، أو عدم حدوث تلامس بينهما، كما في التصادم بين الجسيمات المشحونة على المستوى المجهري، مثل تصادم بروتون بجسيم ألفا (نواة ذرة الهيليوم). وفي هذه الحالة نظرا لأن كلا الجسيمين مشحونان بشحنة موجبة، فإنهما يتنافران عندما يقتربان من بعضهما، دون الحاجة إلى تلامسهما. |
|
|
تصادم جسمين على المستوى الجاهري (يمكن رؤيتهما بالعين المجردة). |
تصادم جسمين مشحونين على المستوى دون الجاهري ( دون تلامس ). |
|
التصادمات والطاقة الحركية Collisions and Kinetic Energy يكون الزخم الخطي محفوظٌ دائما عند تصادم الأجسام أو انفصالها بعضها عن بعض في الأنظمة المعزولة، فهل تكون الطاقة الحركية الخطية محفوظة أيضا في هذه التصادمات؟ الطاقة الحركية الخطية Linear Kinetic Energy الطاقة الحركية الخطية لجسم هي الطاقة المرتبطة بحركته عند انتقاله من مكان إلى آخر؛ حركة انتقالية، وتعتمد على كل من: كتلة الجسم ومقدار سرعته ويعبر عنها بالمعادلة الآتية:
وتوضح هذه المعادلة أن الطاقة الحركية تتناسب طرديا مع كل من: كتلة الجسم، ومربع سرعته. |
||
|
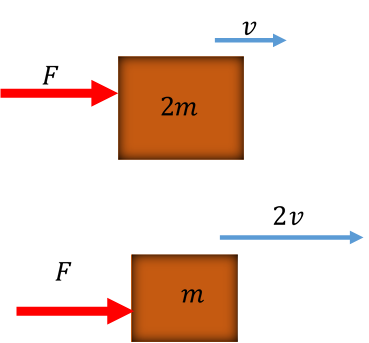
سؤال: صندوقان (A و B) يستقران على سطح أفقي أملس . أثرت في كل منهما القوة نفسها للفترة الزمنية نفسها . إذا علمت أن كتلة الصندوق (A) ضعف كتلة الصندوق (B). أقارن بين : زخميهما وطاقتهما الحركية في نهاية الفترة الزمنية لتأثير القوة . الحل: بالرجوع إلى العلاقة ، وبما أن الصندوقين تأثرا بالقوة نفسها، للفترة الزمنية نفسها؛ فإنهما يتأثران بالدفع نفسه، فيكون لهما التغير في الزخم نفسه. وبما أن الزخم الابتدائي لكليهما يساوي صفر؛ فيكون لهما الزخم النهائي نفسه . الصندوقان مختلفان في الكتلة ومختلفان في السرعة، لذا لمقارنة طاقتيهما الحركية يجب أولا التوصل إلى علاقة بين سرعتيهما، بالاعتماد على أنهما متساويان في الزخم:
نحسب الطاقة الحركية لكل جسم من العلاقة: فنتوصل إلى:
الطاقة الحركية للصندوق (B) ضعف الطاقة الحركية للصندوق (A). |
 |
|
|
حفظ الطاقة الحركية Conservation of kinetic energy قد تكون الطاقة الحركية للأجسام المتصادمة محفوظة، وقد تكون غير محفوظة؛ اعتمادا على نوع التصادم. فإذا لم تكن الطاقة الحركية محفوظة فهذا يعني أن جزءا منها تحول إلى شكل أو أشكال أخرى للطاقة، مثل الطاقة الحرارية والطاقة الصوتية. وتصنف التصادمات بحسب حفظ الطاقة الحركية إلى نوعين رئيسين هما: التصادم المرن، والتصادم غير المرن. وستقتصر دراستنا على التصادم في بعد واحد One -dimensional collision حيث يتحرك الجسمان قبل التصادم على امتداد الخط المستقيم نفسه، ويتصادمان رأسا برأس، بحيث تبقى حركتهما بعد التصادم على المسار المستقيم نفسه.
|
||
|
التصادم المرن Elastic collision في التصادم المرن يكون مجموع الطاقة الحركية لأجزاء النظام قبل التصادم مساويا مجموع الطاقة الحركية بعد التصادم؛ أي أن الطاقة الحركية للنظام محفوظة. ومن الأمثلة عليها التصادم بين كرات البلياردو. وهنا نهمل خسران جزء صغير من الطاقة على شكل طاقة صوتية مثلا. وعند تصادم جسمين(A) و (B) تصادما مرنا، نطبق معادلتي حفظ الزخم وحفظ الطاقة الحركية عليهما كما يأتي: تطبيق قانون حفظ الزخم الخطي: تطبيق قانون حفظ الطاقة: |
في التصادم المرن:
|
|
التصادم غير المرن Inelastic Collision في التصادم غير المرن لا يكون مجموع الطاقة الحركية لأجزاء النظام قبل التصادم مساويا مجموع طاقتها الحركية بعد التصادم؛ أي أن الطاقة الحركية للنظام غير محفوظة. ومن أمثلتها اصطدام كرة مطاطية بسطح صلب (مضرب مثلا)، حيث تفقد جزءا من طاقتها الحركية عندما تتشوه الكرة في أثناء ملامستها للسطح. لكن الزخم الخطي يكون محفوظا في كل أنواع التصادمات التي تكون فيها القوى الخارجية المؤثرة في النظام (إن وجدت) صغيرة جدا مقارنة بقوى الفعل ورد الفعل المتبادلة بين الأجسام المتصادمة. وعند تصادم جسمين (A) و (B) تصادما غير مرن، نطبق معادلة حفظ الزخم، ونحسب الطاقة الحركية المفقودة كما يأتي: تطبيق قانون حفظ الزخم الخطي: الطاقة الحركية المفقودة في التصادم:
|
في التصادم غير المرن:
تتشوه الكرة أثناء ملامستهما للسطح الصلب فتفقد جزءا من طاقتها الحركية. |
|
التصادم عديم المرونة Perfectly Inelastic Collision يوصف التصادم غير المرن بأنه تصادم عديم المرونة عندما تلتحم الأجسام المتصادمة معا بعد التصادم ، لتصبح جسما واحدا تساوي كتلته مجموع كتل الأجسام المتصادمة. ومثال ذلك ما يحدث عند اصطدام كرتي صلصال معا، أو اصطدام سيارتين وتحركهما معا بعد التصادم. وتحسب السرعة النهائية لتصادم عديم المرونة بين جسمين بتطبيق قانون حفظ الزخم الخطي على النظام المكون منهما كما يأتي:
وتحسب الطاقة الحركية المفقودة في التصادم كما يأتي:
|
في التصادم غير المرن: - الزخم الخطي محفوظ. -الطاقة الحركية غير محفوظة الأجسام بعد التصادم تلتحم.
|
|
أفكر : عند تصادم جسمين في بعد واحد تصادما عديم المرونة، ما الشرط الضروري لتفقد الطاقة الحركية الابتدائية للنظام بعد الاصطدام؟ الحل: كي تفقد الطاقة الحركية الابتدائية كاملة بعد التصادم، فهذا يعني أن الطاقة الحركية النهائية للنظام تساوي صفر ؛ ويتحقق ذلك عندما تكون السرعة النهائية للنظام تساوي صفر:
وبالرجوع إلى العلاقة: ، وكي تكون ، يجب أن يكون الزخم الخطي الابتدائي للنظام يساوي صفر؛ وكي يتحقق ذلك فإن الزخم الابتدائي للجسم الأول يكون مساويا في المقدار للزخم الخطي الابتدائي للجسم الثاني ومعاكسا له في الاتجاه . |
|
أتحقق: أقارن بين التصادم المرن، والتصادم غير المرن، والتصادم عديم المرونة من حيث: حفظ الزخم الخطي، حفظ الطاقة الحركية، التحام الأجسام بعد التصادم.
|
|
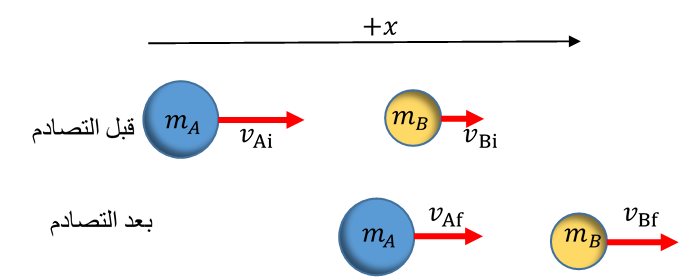
المثال (6) تتحرك الكرة (ِِ A) باتجاه محور بسرعة ؛ كما يبين الشكل، فتصطدم رأسا برأس بكرة أخرى (B)أمامها تتحرك باتجاه محور بسرعة .بعد التصادم تحركت الكرة (B) بسرعة مقدارها بالاتجاه نفسه قبل التصادم. إذا علمت أن ، فأجيب عما يأتي: أ. أحسب سرعة الكرة (A) بعد التصادم، وأحدد اتجاهها. ب. أحدد نوع التصادم.
المعطيات: المطلوب: ، نوع التصادم ؟ الحل: أ. أختار نظام إحداثيات يكون فيه الاتجاه الموجب باتجاه محور ، وأطبق قانون حفظ الزخم الخطي :
ب. لتحديد نوع التصادم يلزم حساب التغير في الطاقة الحركية:
بما أن التغير في الطاقة الحركية للنظام سالب، فهذا يعني حدوث نقص في الطاقة الحركية، والكرتان لم تلتحما بعد التصادم، إذا التصادم غير مرن. |
|
المثال (7) كرتا بلياردو كتلة كل منهما . تتحرك الكرة الزرقاء (A)باتجاه محور بسرعة نحو الكرة الحمراء (B)الساكنة وتتصادمان رأسا برأس تصادما مرنا. أحسب مقدار سرعة الكرة (B) بعد التصادم وأحدد اتجاهها. |
|
المعطيات : المطلوب: الحل: أختار نظام إحداثيات يكون فيه الاتجاه الموجب باتجاه محور وأطبق قانون حفظ الزخم الخطي على نظام الكرتين. لأن فإنها تختصر من المعادلة : المعادلة (1) فيها كميتان مجهولتان، لذا يلزم معادلة أخرى نحصل عليها من تطبيق قانون حفظ الطاقة الحركية؛ لأن التصادم مرن.
بتعويض المعادلة (1) في المعادلة (2) لإيجاد مقدار نحصل على ما يأتي:
وبحل هذه المعادلة نتوصل أن لها حلين ؛ الأول والثاني . الحل الأول: يوضح أن سرعة الكرة (B) بعد التصادم باتجاه محور ، وهو نفسه اتجاه حركة الكرة (A) قبل التصادم. الحل الثاني : مرفوض، لأنه بتعويض في المعادلة (1) نجد أن ، أي أن الكرة (A) اخترقت الكرة (B) واستمرت في الحركة باتجاه وهذا غير ممكن. أي أن و ؛هذا يعني أن الكرة (A)سكنت بعد التصادم ، بينما اكتسبت الكرة (B) السرعة الابتدائية للكرة (ِ A). نستنتج مما سبق ما يأتي: عندما تتصادم كرة متحركة مع كرة ساكنة، مساوية لها في الكتلة، تصادما مرنا، تتوقف الكرة المتحركة وتكتسب الكرة الساكنة السرعة الابتدائية للكرة المتحركة قبل التصادم.
|
|
تطبيق : البندول القذفي يستخدم البندول القذفي لقياس مقدار سرعة مقذوف، مثل الرصاصة. إذ تطلق رصاصة كتلتها باتجاه كتلة ساكنة كبيرة من الخشب كتلتها معلقة رأسيا بخيطين خفيفين. فتخترق الرصاصة قطعة الخشب وتستقر داخلها، ويتحرك النظام المكون منهم كجسم واحد، ويرتفع مسافة رأسية . ويمكن حساب مقدار سرعة الرصاصة قبل اصطدامها بقطعة الخشب بمعرفة مقدار . |
|
 |
 |
|
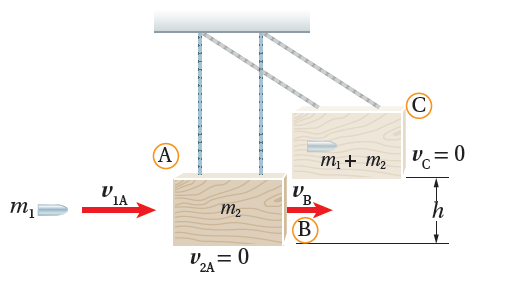
يبين الشكل الأول حركة بندول قذفي بعد اختراق سهم له. ويمثل الشكل الثاني رسما لبندول تخترقه رصاصة، حيث يشير الرمز (A)للنظام قبل التصادم مباشرة والرمز(B) يمثل النظام بعد التصادم مباشرة، أما الرمز (C) فيمثل النظام عند أقصى ارتفاع (h).ويتضح من الشكل أن اتجاه حركة النظام المكون من قطعة الخشب والرصاصة بعد التصادم مباشرة يكون باتجاه حركة الرصاصة نفسه قبل التصادم في مستوى الصفحة ونحو اليمين. بتطبيق قانون حفظ الزخم الخطي على النظام قبل التصادم مباشرة وبعد التصادم مباشرة، نحسب، وتمثل سرعة النظام المكون من قطعة الخشب والرصاصة بعد التصادم مباشرة :
بعد التصادم مباشرة يتحرك النظام من النقطة (B) وصولا إلى أقصى ارتفاع (h) عند الموقع (C)، وبما أنه لا توجد قوى غير محافظة تبذل شغلا على النظام ؛ لذا تكون الطاقة الميكانيكية للنظام محفوظة، حيث الطاقة الميكانيكية تساوي مجموع الطاقة الحركية وطاقة الوضع الناشئة عن الجاذبية الارضية :
بافتراض أن النقطة (B) هي مستوى الإسناد، فإن طاقة الوضع الناشئة عن الجاذبية الأرضية لقطعة الخشب لحظة بدء حركتها عند النقطة (B) تساوي صفر ، كما أن الطاقة الحركية عند أقصى ارتفاع تساوي صفر ، وبالتعويض في المعادلة السابقة:
بحذف من طرفي المعادلة، وتعويض من معادلة حفظ الزخم : وبأخذ الجذر التربيعي لطرفي المعادلة، وإعادة ترتيب الحدود:
تستخدم العلاقة التي توصلنا إليها لحساب سرعة إطلاق جسم مقذوف مثل رصاصة أو سهم. |
|
|
المثال (8) أطلق سعد سهما كتلته أفقيا باتجاه بندول قذفي كتلته فاصطدم به والتحما معا بحيث كان أقصى ارتفاع وصل إليه البندول فوق المستوى الإبتدائي له يساوي . باعتبار تسارع االسقوط الحر أجيب عما يأتي: أ. أي مراحل حركة النظام المكون من البندول والسهم يكون فيها الزخم الخطي محفوظا؟ ب. أي مراحل حركة النظام تكون فيها الطاقة الميكانيكة محفوظة؟ ج. أحسب مقدار السرعة الابتدائية للسهم. المعطيات : أفترض رمز كتلة البندول(A) ورمز السهم (B) , المطلوب: الحل: أ. يكون الزخم الخطي محفوظا في التصادم عديم المرونة بين السهم والبندول. ب. تكون الطاقة الميكانيكية محفوظة للسهم قبل التصادم، كما تكون الطاقة الميكانيكية للنظام محفوظة للبندول والسهم بدءًا من حركتهما معا بعد التصادم مباشرة، وحتى وصولهما إلى أقصى ارتفاع، وذلك عند إهمال قوى الاحتكاك. ج. تحسب السرعة الابتدائية للسهم باستخدام العلاقة :
|
|
المثال (9) عربة قطار (A) كتلتها تتحرك في مسار افقي مستقيم لسكة حديد بسرعة مقدارها باتجاه محور فتصطدم بعربة أخرى (B) كتلتها تقف على المسار نفسه، وتلتحمان معا وتتحركان على المسار المستقيم لسكة الحديد أجيب عما يأتي: أ. أحسب مقدار سرعة عَربتَي القطار بعد التصادم وأحدد اتجاهها. ب. ما نوع التصادم؟ وهل الطاقة الحركية محفوظة في هذا النوع من التصادمات؟ أبرر إجابتي. |
|
المعطيات: المطلوب ، نوع التصادم ؟ ، هل الطاقة الحركية محفوظة؟ الحل: نختار نظام إحداثيات يكون فيه المحور الموجب باتجاه أ. باستخدام قانون حفظ الزخم الخطي:
ب. بما أن عربتي القطار التحمتا بعد التصادم فهو تصادم عديم المرونة. وفي هذا النوع من التصادمات تكون الطاقة الحركية غير محفوظة، ويمكن التأكد من ذلك عن طريق مقارنة الطاقة الحركية لنظام العربتين قبل التصادم بالطاقة الحركية للنظام بعد التصادم.
التغير في الطاقة الحركية سالب؛ أي أن الطاقة الحركية غير محفوظة، والعربتان التحمتا معا بعد التصادم ، لذا فإن التصدم عديم المرونة. |
|
تمرين أطلق محقق رصاصة كتلتها أفقيا باتجاه بندول قذفي كتلته فاصطدمت به والتحما معا ، فكان أقصى ارتفاع وصل إليه البندول فوق المستوى الابتدائي له . أحسب مقدار السرعة الابتدائية للرصاصة. الحل:
|
|
تمرين تظهر في الشكل لعبة شهيرة تسمى كرات نيوتن؛ تتكون من كرات عدة فلزية متماثلة متراصة معلقة بخيوط خفيفة ، عند سحب إحدى الكرات الفلزية الخارجية نحو الخارج ثم إفلاتها؛ فإنها تصطدم تصادما مرنا بالكرة التي كانت مجاورة لها، وبدلا من حركة هذه الكرة، نلاحظ أن الكرة الخارجية على الجانب الآخر من اللعبة تقفز في الهواء. أ. أفسر ما الذي حدث. ب. أتوقع ماذا سيحدث إذا سحبت كرتين من الجانب الأيسر جانبيا ثم افلتهما معا. ج. أتوقع ماذا سيحدث إذا رفعت الكرتين الخارجيتين كلتيهما على الجانبين إلى الارتفاع نفسه وأفلتهما في اللحظ نفسها. الحل: أ. توضح اللعبة قانون حفظ الزخم، فالكرات متراصة لا يوجد فراغ بينها يسمح بحركتها، وبحسب قانون حفظ الزخم الخطي ينتقل الزخم الخطي من كرة إلى أخرى حتى يصل الكرة التي على الجانب الآخر فتقفز في الهواء. ب. بما أن الكرات متماثلة والتصادم مرن، فإنه سيقفز كرتين من الجانب الآخر حسب قانون حفظ الزخم الخطي. ج. يكون الزخم الخطي الابتدائي صفر ا ؛ لأن الكرتين تتحركان باتجاهين متعاكسين وبالسرعة نفسها، فيكون الزخم الخطي الكلي النهائي صفرا أيضا ولن تقفز أي كرة. |
عند سحب كرة جانبا وإفلاتها ، تصطدم بالكرات الساكنة فتقفز الكرة الخارجية على الجانب الآخر من اللعبة، لتصل إلى أقصى ارتفاع، ثم تتحرك نحو الكرات المتراصة، فتصطدم بها، فتقفز الكرة الساكنة على الطرف الأول من اللعبة، وهكذا.... 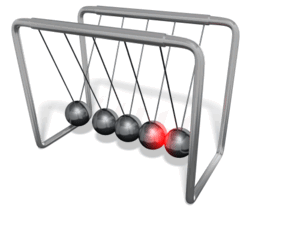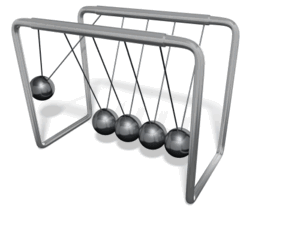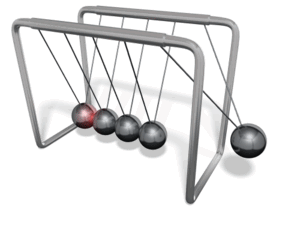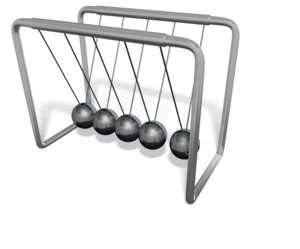 عند سحب كرتين و إفلاتهما معا، تتحرك كرتان من الجانب الآخر للعبة . 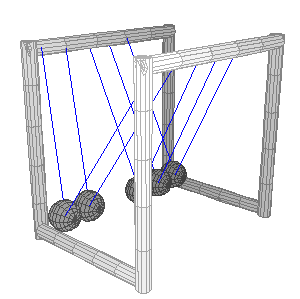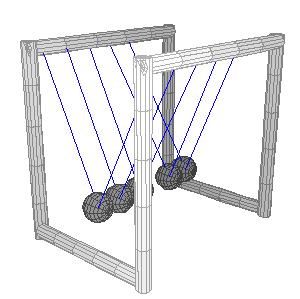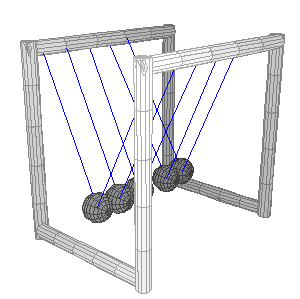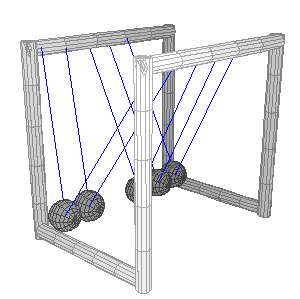 |