التكامل المحدود

التكامل المحدود

 تعرفنا في الدرس السابق إلى التكامل غير المحدود للاقتران f(x) ($\int f\left(x\right)dx$) وقواعد هذا التكامل.

سنتعرف في هذا الدرس إلى التكامل المحدود للاقتران f (x) وخصائص هذا الاقتران.

يسمى ${\int }_a^{b}f\left(x\right) dx$ بالتكامل المحدود للاقتران f (x) حيث أن a هي الحد السفلي للتكامل و b هي الحد العلوي للتكامل.

 

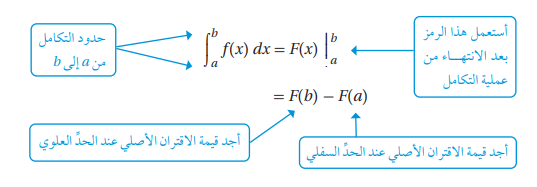
ملاحظة: في التكامل المحدود لا يوجد ثابت للتكامل (C) وذلك لأن الناتج نفسه بغض النظر عن الاقتران الأصلي.

$$\begin{gathered} {\int }_a^{b}f\left(x\right) dx=\left[F\left(b\right) +C\right]-\left[F\left(a\right)+C\right] \\ =F\left(b\right)-F\left(a\right) \end{gathered}$$

مثال: أجد كل من التكاملات الآتية:

$$\begin{gathered} 1){\int }_{-1}^1{x}^4 dx=\frac{x^5}{5}{|}_{-1}^1 \\ = (\frac{1^5}{5})-(\frac{-1^5}{5})=\frac{1}{5}-(\frac{-1}{5})=\frac{2}{5} \end{gathered}$$

$2\left){\int }_2^5\right(2x-1)=\frac{1}{2}\frac{{(2x-1)}^2}{2}{|}_2^5=\frac{{(2x-1)}^2}{4}{|}_2^5=\frac{(2{\left(5\right)-1)}^2}{4}-\frac{(2{\left(2\right)-1)}^2}{4}=\frac{81}{4}-\frac{9}{4}=\frac{72}{4}=18$

قواعد التكامل المحدود 

إذا كان f (x) وg (x) اقترانين متصلين على الفترة $\left[a,b\right]$، وكان k ثابتا، فإن:

 

$1\left){\int }_a^{b}kf\right(x) dx=k{\int }_a^{b}f(x) dx$                        تكامل الاقتران المضروب في ثابت

مثال:

${\int }_{-1}^{1}3x^2 dx=3{\int }_{-1}^1{x}^2 dx=3\frac{x^3}{3}{|}_{-1}^{ 1}=x^3{|}_{-1}^{ 1}={\left(1\right)}^3-{(-1)}^3=1+1=2$

$2) {\int }_a^b(f\left(x\right)\pm g\left(x\right)) dx={\int }_a^{b}f(x) dx\pm {\int }_a^{b}g(x) dx$       تكامل المجموع أو الفرق

مثال:

إذا كان ${\int }_1^{3}f\left(x\right) dx=7$وكان ${\int }_1^{3}g\left(x\right) dx=-1$

 فجد قيمة: ${\int }_1^3\left(2f\right(x)-3g(x\left)\right) dx$

${\int }_1^3\left(2f\right(x)-3g(x\left)\right) dx=2{\int }_1^{3}f\left(x\right) dx-3{\int }_1^{3}g\left(x\right) dx=2\left(7\right)-3(-1)=14+3=17$

$3) {\int }_a^{a}f(x) dx=0$                                                                          التكامل عند النقطة

مثال:

اجد قيمة ${\int }_{-4}^{-4}{(x^2-3x)}^5 dx$

${\int }_{-4}^{-4}{(x^2-3x)}^5 dx=0$

$4) {\int }_a^{b}f(x) dx=-{\int }_b^{a}f(x) dx$                                                 عكس حدود التكامل

مثال:

اذا كان ${\int }_3^{4}f\left(x\right) dx=\frac{3}{2}$اجد ${\int }_4^{3}8f\left(x\right) dx$

$=8(-{\int }_3^{4}f(x) dx)=8(-(\frac{3}{2}\left)\right)=4(-3)=-12$

$5) {\int }_a^{b}f(x) dx={\int }_a^{c}f(x) dx+{\int }_c^{b}f(x) dx$                                     تجزئة التكامل

مثال:

اذا كان ${\int }_1^{4}f\left(x\right) dx=-5$وكان ${\int }_1^{7}f\left(x\right) dx=3$اجد ${\int }_7^{4}f\left(x\right) dx$

${\int }_7^{4}f\left(x\right) dx={\int }_7^{1}f\left(x\right) dx+{\int }_1^{4}f\left(x\right) dx=-3+-5=-8$

تطبيقات التكامل

المساحة:

يمكننا ايجاد المساحة المحصورة بين منحنى الأقتران f(x) والمستقيمين x=a و x=b والمحور x باستخدام التكامل حيث ان هذه المساحة تساوي 

$A={\int }_a^{b}f\left(x\right) dx$

وهناك ثلاث حالات لهذه المنطقة المحصورة وهي 

الحالة الاولى: ان تكون المنطقة المحصورة تقع فوق المحور x حيث نجد المساحة عن طريق التكامل الاتي:

$A={\int }_a^{b}f\left(x\right) dx$

مثال:

اجد مساحة المنطقة المحصورة بينمنحنى الاقتران $f\left(x\right)=1-x^2$ المحور x.

$A={\int }_{-1}^{1}1-x^2 dx$

وحدة مربعة$x-\frac{x^3}{3}{|}_{-1}^{ 1}=(1-\frac{1}{3})-(-1-\frac{-1}{3})=\frac{2}{3}-\frac{-2}{3}=\frac{4}{3}$

 

الحالة الثانية: ان تكون المنطقة المحصورة تقع تحت المحور x حيث نجد المساحة عن طريق التكامل الأتي:

$A=-{\int }_a^b f\left(x\right) dx$

مثال:

اجد مساحة المنطقة المحصورة بين منحنى الاقتران $f\left(x\right)=x^2-4$ والمحور x.

$$\begin{gathered} A=-{\int }_{-2}^2{x}^2-4 dx=-(\frac{x^3}{3}-4x){|}_{-2}^{ 2} \\ -\left[\right(\frac{8}{3}-8)-(\frac{-8}{3}+8\left)\right] \\ -[-\frac{16}{3}-\frac{16}{3}]=-(-\frac{32}{3}) \end{gathered}$$

وحدة مربعة$=\frac{32}{3}$

الحالة الثالثة: اذا وقع جزء من المنطقة المحصورة فوق المحور x والجزء الاخر تحت محور x في هذه الحالة يتم تحديد المقطع x للاقتران ثم ايجاد المساحة باستعمال القاعدة الاتية:

$A=-{\int }_a^{c}f\left(x\right) dx+{\int }_c^{b}f\left(x\right) dx$

مثال:

اجد مساحة المنطقة المحصورة بين منحنى الاقتران $f\left(x\right)=x-2$ ومحور السينات والمستقيمين $x=0 , x=4$.

$$\begin{gathered} A=-{\int }_0^2(x-2) dx+{\int }_2^4(x-2) dx=-(\frac{x^2}{2}-2x){|}_0^2+(\frac{x^2}{2}-2x){|}_2^4 \\ -(2-4)+\left(\right(8-4)-(2-4\left)\right) \\ 2+4+2 \end{gathered}$$

وحدة مربعة$=8$

الحجوم الدورانية:

يمكن ايجاد حجم مجسم ناتج عن دوران جزء من اقتران حول المحور x ( الحجوم الدورانية)باستخدام التكامل حيث ان:

حجم المجسم الناتج من دوران جزء من منحنى الاقتران: y=f(x)، واقع بين x=a و x=b، حيث $a<b$ حول المحور x، هو: $V={\int }_a^b\mathrm{\pi }(\mathrm{f}{\left(\mathrm{x}\right))}^2 \mathrm{dx}$            و                             $V={\int }_a^b{\mathrm{\pi y}}^2 \mathrm{dx}$

مثال:

اجد حجم المجسم الناتج من دوران المنطقة المحصورة بين المحور x ومنحنى الاقتران $y=x^2-4$ حول محور  x.

$v={\int }_{-2}^2\mathrm{\pi }{\left(\mathrm{y}\right)}^2 \mathrm{v}={\int }_{-2}^2\mathrm{\pi }{({\mathrm{x}}^2-4)}^2 \mathrm{dx} \mathrm{\pi }{\int }_{-2}^2({\mathrm{x}}^4-8{\mathrm{x}}^2+16) \mathrm{dx}=\mathrm{\pi }(\frac{{\mathrm{x}}^5}{5}-\frac{8{\mathrm{x}}^3}{3}+16\mathrm{x}){|}_{-2}^{ 2}=34.1\mathrm{\pi }$