التكامل المحدود
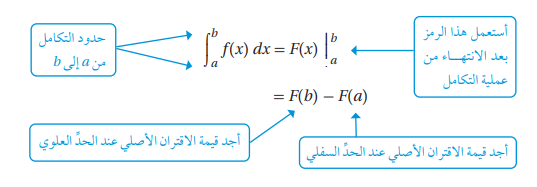
يمكننا إيجاد التكامل المحدود كما هو موضح بالشكل الآتي:
قواعد التكامل المحدود
إذا كان f (x) و g (x) اقترانين متصلين على الفترة وكان k ثابتاً، فإن:
|
تكامل الاقتران المضروب في ثابت |
| تكامل المجموع أو الفرق |
| التكامل عند النقطة |
| عكس حدود التكامل |
| تجزئة التكامل |
المساحة
يمكننا إيجاد المساحة باستخدام التكامل المحدود.
|
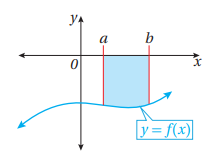
مساحة المنطقة المحصورة بين منحنى الاقتران f (x)، والمحور x، والمستقيمين: x=a، x=b الواقعة فوق المحور x.
|
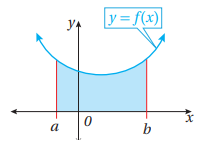
مساحة المنطقة المحصورة بين الاقتران f (x)، والمحور x، والمستقيمين: x=b، x=a الواقعة أسفل المحور x.
|
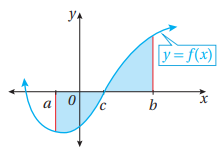
مساحة المنطقة المحصورة بين الاقتران f (x)، والمحور x، والمستقيمين: x=b، x=a والتي يقع جزء منها فوق المحور x والجزء الآخر تحته.
|
الحجوم الدورانية
يمكننا إيجاد الحجوم الدورانية باستخدام التكامل المحدود.
|
حجم المجسم الناتج من دوران جزء من منحنى الاقتران: ، واقع بين x=b، x=a، حيث حول المحور x، هو: or |