رياضيات فصل ثاني

أتحقق من فهمي

ص:22

أجد كلا من التكاملين الاتيين:

$a) {\int }_{-1}^1{x}^4 dx$

${\int }_{-1}^1{x}^4 dx=\frac{x^5}{5}{|}_{-1}^{ 1}=\frac{{\left(1\right)}^5}{5}-\frac{{(-1)}^5}{5}=\frac{1}{5}-\frac{-1}{5}=\frac{2}{5}$

$b) {\int }_{-2}^3(3x^2-4x+1) dx$

${\int }_{-2}^3(3x^2-4x+1) dx=x^3-2x^2+x {|}_{-2}^{ 3}=\left(\right(3^3)-2{\left(3\right)}^2+3)-({(-2)}^3-2{(-2)}^2+-2)=12+18=30$

أتحقق من فهمي

ص:24

اذا كان: ${\int }_{-1}^{1}f\left(x\right) dx=5, {\int }_4^{1}f\left(x\right) dx=2, {\int }_{-1}^{1}h\left(x\right) dx=7$، فأجد كلا مما يأتي:

$a) {\int }_{-1}^1(f\left(x\right)+3h\left(x\right)) dx$

${\int }_{-1}^1\left(f\right(x)+3h(x\left)\right) dx={\int }_{-1}^{1}f\left(x\right) dx+3{\int }_{-1}^{1}h\left(x\right) dx=5+3\left(7\right)=26$

$b) {\int }_{-1}^{4}f(x) dx$

${\int }_{-1}^{4}f\left(x\right) dx={\int }_{-1}^{1}f\left(x\right) dx+{\int }_1^{4}f\left(x\right) dx=5+(-2)=3$

أتحقق من فهمي

ص:27

a) أجد مساحة المنطقة الحصورة بين منحنى الاقتران: $f\left(x\right)=2\sqrt{x}$، والمحور x، والمستقيمين: x=1 و x=4.

$A={\int }_1^{4}2\sqrt{x} dx=2\left(\frac{2}{3}\right)x^{\frac{3}{2}}{|}_1^4=\frac{4}{3}\sqrt{x^3}{|}_1^4=\frac{4}{3}\sqrt{4^3}-\frac{4}{3}\sqrt{13}=\frac{4}{3}\left(8\right)-\frac{4}{3}=\frac{28}{3}$

b) أجد مساحة المنطقة المحصورة بين منحنى الاقتران: $f\left(x\right)=x^2-4$، والمحور x.

$A=-{\int }_{-2}^2{x}^2-4 dx=-(\frac{x^3}{3}-4x){|}_{-2}^{ 2}=-(\frac{8}{3}-8)-(\frac{-8}{3}+8)=-(\frac{16}{3}-16)=1.6-\frac{16}{3}=\frac{32}{3}$

أتحقق من فهمي

ص:28

أجد مساحة المنطقة المحصورة بين منحنى الاقتران: $f\left(x\right)=x^3-9x$، والمحور x.

$A={\int }_{-3}^0(x^3-9x) dx+(-{\int }_0^3(x^3-ax) dx)=\frac{x^4}{4}-\frac{a{x}^2}{2}{|}_{-3}^{ 0}+\frac{-x^4}{4}+\frac{a{x}^2}{2}{|}_0^3=(0-(\frac{81}{4}-\frac{81}{2}\left)\right)+\left(\right(\frac{-81}{4}+\frac{81}{2})-0)=\frac{81}{4}+\frac{81}{4}=\frac{162}{4}=\frac{81}{2}$

أتحقق من فهمي

ص:30

أجد حجم المجسم الناتج من دوران المنطقة المحصورة بين المحور x ومنحنى الاقتران: $y=x^2-1$ حول المحور x.

$$\begin{gathered} y=0 \\ {x}^2-1=0 \\ x=\pm 1 \\ v={\int }_{-1}^1\mathrm{\pi }{({\mathrm{x}}^2-1)}^2 \mathrm{dx}=\mathrm{\pi }{\int }_{-1}^1({\mathrm{x}}^4-2{\mathrm{x}}^2+1) \mathrm{dx}=\mathrm{\pi }[\frac{{\mathrm{x}}^5}{5}-\frac{2{\mathrm{x}}^3}{3}+\mathrm{x}]{|}_{-1}^{ 1} \\ =\mathrm{\pi }\left[\right(\frac{1}{5}-\frac{2}{3}+1)-(-\frac{1}{5}+\frac{2}{3}-1\left)\right]=\mathrm{\pi }[\frac{1}{5}-\frac{2}{3}+1+\frac{1}{5}-\frac{2}{3}+] \\ =\mathrm{\pi }[\frac{2}{5}-\frac{2}{3}+2]=\mathrm{\pi }\left[\frac{6-10+30}{15}\right]=\frac{26}{15}\mathrm{\pi } \end{gathered}$$

أتدرب وأحل المسائل

أجد كل من التكاملات الأتية:

$1) {\int }_{-1}^{3}3x^2 dx$

${\int }_{-1}^{1}3x^2 dx=x^3{|}_{-1}^{ 3}=27--1=28$

$2) {\int }_1^{5}10x^{-2} dx$

${\int }_1^{5}10x^{-2} dx=\frac{-10}{x}{|}_1^5=\frac{-10}{5}-\frac{-10}{1}=-2+10=8$

$3) {\int }_0^2(3x^2+4x+3) dx$

${\int }_0^2(3x^2+4x+3) dx=x^3+2x^2+3x{|}_0^2=(8+8+6)-\left(0\right)=22$

$4) {\int }_2^{5}3x(x+2) dx$

${\int }_2^{5}3x(x+2) dx={\int }_2^5(3x^2+6x) dx=x^3+3x^2{|}_2^5=(125+75)-(8+12)=200-20=180$

$5) {\int }_1^{8}8\sqrt[3]{x} dx$

${\int }_1^{8}8\sqrt[3]{x} dx={\int }_1^8{x}^{\frac{1}{3}} dx=8\left(\frac{3}{4}\right)x^{\frac{4}{3}}{|}_1^8=6\sqrt[3]{x^4}{|}_1^8=6\sqrt[3]{8^4}-6\sqrt[3]{14}=6\left(16\right)-6=96-6=90$

$6) {\int }_1^9(\sqrt{x}-\frac{4}{\sqrt{x}}) dx$

$$\begin{gathered} {\int }_1^9(\sqrt{x}-\frac{4}{\sqrt{x}}) dx={\int }_1^9(x^{\frac{1}{2}}-4x^{\frac{-1}{2}}) dx=\frac{2}{3}{x}^{\frac{3}{2}}-8x^{\frac{1}{2}}{|}_1^9=\frac{2}{3}\sqrt{x^3}-8\sqrt{x}{|}_1^9 \\ =(\frac{2}{3}\sqrt{9^3}-8\sqrt{a})-(\frac{2}{3}\sqrt{13}-8\sqrt{1})=(18-24)-(\frac{2}{3}-8)=-6-\frac{-22}{3}=\frac{-18}{3}+\frac{22}{3}=\frac{4}{3} \end{gathered}$$

$7) {\int }_1^2{(2x-4)}^4 dx$

${\int }_1^2{(2x-4)}^4 dx=\frac{1}{10}{(2x-4)}^5{|}_1^2=0-(-\frac{32}{10})=3.2$

$8) {\int }_0^4\frac{1}{\sqrt{6x+1}} dx$

$$\begin{gathered} {\int }_0^4\frac{1}{\sqrt{6x+1}} dx={\int }_0^4{(6x+1)}^{-\frac{1}{2}} dx=\frac{2}{6}{(6x+1)}^{\frac{1}{2}}{|}_0^4=\frac{1}{3}(\sqrt{6\left(4\right)+1}-\sqrt{6\left(0\right)+1}) \\ =\frac{1}{3}(5-1)=\frac{4}{3} \end{gathered}$$

$9) {\int }_1^3(x-2\left)\right(x+2) dx$

${\int }_1^3(x-2)(x+2) dx={\int }_1^3(x^2-4) dx=\frac{x^3}{3}-4x{|}_1^3=(\frac{27}{3}-12)-(\frac{1}{3}-4)=-3-\frac{-11}{3}=\frac{-9}{3}+\frac{11}{3}=\frac{2}{3}$

اذا كان: ${\int }_1^{5}g\left(x\right) dx=8و،{\int }_1^{5}f\left(x\right) dx=6و،{\int }_1^{2}f\left(x\right) dx=-4$، فأجد كلا مما يأتي:

$10) {\int }_2^{2}g(x) dx$

${\int }_2^{2}g\left(x\right) dx=0$

$11) {\int }_5^{1}g(x) dx$

${\int }_5^{1}g\left(x\right) dx=-{\int }_1^{5}g\left(x\right) dx=-8$

$12) {\int }_1^{2}3f(x) dx$

${\int }_1^{2}3f\left(x\right) dx=3{\int }_1^{2}f\left(x\right) dx=3(-4)=-12$

$13) {\int }_2^{5}f(x) dx$

${\int }_2^{5}f\left(x\right) dx={\int }_2^{1}f\left(x\right) dx+{\int }_1^{5}f\left(x\right) dx=4+6=10$

$14) {\int }_1^5(f\left(x\right)-g\left(x\right)) dx$

${\int }_1^5\left(f\right(x)-g(x\left)\right) dx={\int }_1^{5}f\left(x\right) dx-{\int }_1^{5}g\left(x\right) dx=6-8=-2$

$15) {\int }_1^5(4f\left(x\right)+g\left(x\right)) dx$

${\int }_1^5\left(4f\right(x)+g(x\left)\right) dx=4{\int }_1^{5}f\left(x\right) dx+{\int }_1^{5}g\left(x\right) dx=4\left(6\right)+8=24+8=32$

أحل الاسئلة الثلاثة الاتية تباعا:

16) أجد ${\int }_0^1{x}^n dx$، حيث$n>0$.

${\int }_0^1{x}^n dx=\frac{x^{n+1}}{n+1}{|}_0^1=\left(\frac{{\left(1\right)}^{n+1}}{n+1}\right)-\left(\frac{{\left(0\right)}^{n+1}}{n+1}\right)=\frac{1}{n+1}$

17) أثبت أن ${\int }_0^1{x}^n(1-x) dx=\frac{1}{(n+1)(n+2)}$.

$$\begin{gathered} {\int }_0^1{x}^2(1-x) dx={\int }_0^1{x}^n-x^{n+1} dx=\frac{x^{n+1}}{n+1}-\frac{x^{n+2}}{n+2}{|}_0^1=(\frac{{\left(1\right)}^{n+1}}{n+1}-\frac{{\left(1\right)}^{n+2}}{n+2})-\left(0\right) \\ =\frac{1}{(n+1)}-\frac{1}{(n+2)}=\frac{n+2-(n+1)}{(n+1)(n+2)}=\frac{n+2-2-1}{(n+1)(n+2)}=\frac{n+2-n-1}{(n+1)(n+2)}=\frac{1}{(n+1)(n+2)} \end{gathered}$$

18) أجد ${\int }_0^1{x}^n(1-x^2) dx$، ثم أكتب الاجابة في أبسط صورة ممكنة.

${\int }_0^1{x}^n(1-x^2) dx={\int }_0^1{x}^n-x^{n+2} dx=\frac{x^{n+1}}{n+1}-\frac{x^{n+3}}{n+3}{|}_0^1=(\frac{1}{n+1}-\frac{1}{n+3})-\left(0\right)=\frac{n+3-n-1}{(n+1)(n+3)}=\frac{2}{(n+1)(n+3)}$

يمثل الاقتران: $v\left(t\right)=t^2(6-t)$ سرعة سيارة بالمتر لكل ثانية بعد t ثانية من بدء حركتها، حيث: $0\le t\le 6$. اذا تحركت السيارة مدة 6 ثوان، فأجيب عن الأسئلة الأتية:

19) أجد أقصى سرعة للسيارة.

$$\begin{gathered} v\left(t\right)=t^2(6-t)=6t^2-t^3 \\ v\text{'}\left(t\right)=12t-3t^2=3t(4-t) \\ v\text{'}\left(t\right)=0 \\ t=0 or t=4 \\ v\text{'}\text{'}=12-6t \\ v\text{'}\text{'}\left(t\right)12>0 \\ v\text{'}\text{'}\left(4\right)=-12<0 \\ v\left(4\right)=6\times 16-64=32 m/s \end{gathered}$$

20) أمثل منحنى الاقتران v(t) بيانيا.

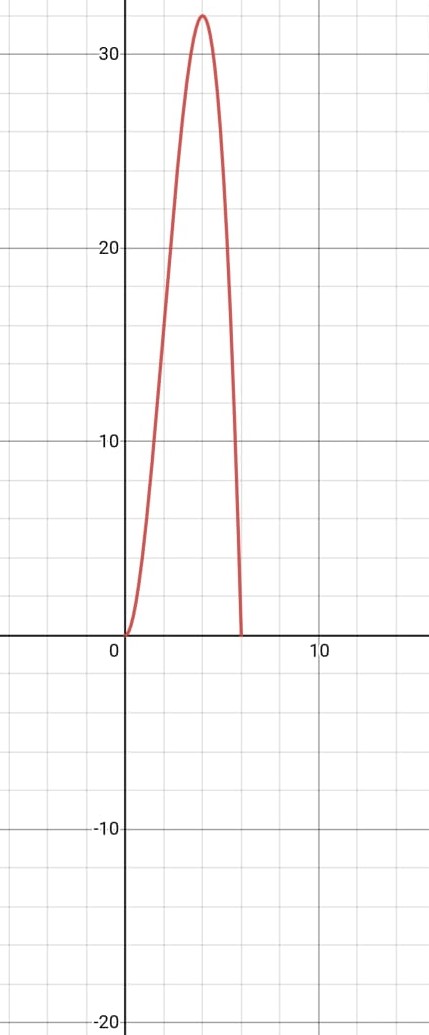
21) أجد المسافة التي قطعتها السيارة.

$s\left(t\right)={\int }_0^{6}v\left(t\right) dt={\int }_0^6(6t^2-t^3) dt=2t^3-\frac{1}{4}{t}^4{|}_0^6=(432-324)-\left(0\right)=108 m$

يبين الشكل المجاور منحنى الاقتران: $f\left(x\right)=x^2-2x$:

22) أجد مساحة المنطقة المحصورة بين منحنى الاقتران، والمحور x.

$A=-{\int }_0^2(x^2-2x) dx=(\frac{1}{3}{x}^3-x^2){|}_0^2=-\left(\right(\frac{8}{3}-4)-(0\left)\right)=\frac{4}{3}$

23) أجد مساحة المنطقة المحصورة بين منحنى الاقتران، والمحور x، والمستقيم x=3.

$$\begin{gathered} A=-{\int }_0^{2}f\left(x\right) dx+{\int }_2^{3}f\left(x\right) dx=-{\int }_0^2(x^2-2x) dx+{\int }_2^3(x^2-2x) dx=-(\frac{1}{3}{x}^3-x^2){|}_0^2+(\frac{1}{3}{x}^3-x^2){|}_2^3 \\ =-\left(\right(\frac{8}{3}-4)-(0\left)\right)+\left(\right(9-9)-(\frac{8}{3}-4\left)\right)=\frac{8}{3} \end{gathered}$$

24) أجد مساحة المنطقة المحصورة بين منحنى الاقتران، والمحور x، والمستقيم x=-1.

$$\begin{gathered} A={\int }_{-1}^{0}f\left(x\right) dx-{\int }_0^{2}f\left(x\right) dx={\int }_{-1}^0(x^2-2x) dx-{\int }_0^2(x^2-2x) dx=(\frac{1}{3}{x}^3-x^2){|}_{-1}^{ 0}-(\frac{1}{3}{x}^3-x^2){|}_0^2 \\ =\left(\right(0)-(-\frac{1}{3}-1\left)\right)-\left(\right(\frac{8}{3}-4)-(0\left)\right)=\frac{8}{3} \end{gathered}$$

25) أجد مساحة المنطقة المحصورة بين منحنى الاقتران: $f\left(x\right)=3x^2-2x+2$، والمحور x، والمستقيمين: x=0 و x=2.

$A={\int }_0^2(3x^2-2x+2) dx=x^3-x^2+2x{|}_0^2=8$

26) أجد مساحة المنطقة المحصورة بين منحنى الاقتران: $f\left(x\right)=a^2-x^2$، والمحور x بدلالة الثابتa، حيث $a>0$.

$A={\int }_{-a}^{a}f\left(x\right) dx={\int }_{-a}^a(a^2-x^2) dx=a^{2}x-\frac{1}{3}{x}^3{|}_{-a}^{ a}=(a^3-\frac{1}{3}{a}^3)-(a^3+\frac{1}{3}{a}^3)=\frac{4}{3}{a}^3$

27) أجد مساحة المنطقة المحصورة بين منحنى العلاقة: $y={(2x+16)}^{\frac{3}{4}}$، والمحورين الاحداثيين.

$$$$\begin{gathered} y={(2x+16)}^{\frac{3}{4}} {(2x+16)}^{\frac{3}{4}}=0 x=-8 \\ A={\int }_{-8}^0{(2x+16)}^{\frac{3}{4}} dx=\frac{2}{7}{(2x+16)}^{\frac{7}{4}}{|}_{-8}^{ 0}=\left(\frac{256}{7}\right)-\left(0\right)=\frac{256}{7}... \end{gathered}$$

28) يبين الشكل المجاور منحنى الاقتران: $y=kx(4-x)$. اذا كانت مساحة المنطقة بين منحنى الاقتران والمحور x هي 32 وحدة مربعة، فأجد قيمة الثابت k.

$$\begin{gathered} y=kx(4-x) \\ kx(4-x)=0 \\ x=0 or x=4 \\ A={\int }_0^4(4kx-k{x}^2) dx=2k{x}^2-\frac{k}{3}{x}^3{|}_0^4=\frac{32}{3}k \\ \frac{32}{3}k=32 \\ k=3 \end{gathered}$$

29) أجد حجم المجسم الناتج من دوران جزء من منحنى الاقتران: $y=0.3x$، يقع بين x=2 و x=5 حول المحور x.

$v={\int }_2^5{\mathrm{\pi y}}^2 \mathrm{dx}={\int }_2^5\mathrm{\pi }{(0.3\mathrm{x})}^2 \mathrm{dx}={\int }_2^{5}0.09{\mathrm{\pi x}}^2 \mathrm{dx}=0.03{\mathrm{\pi x}}^3{|}_2^5=3.75\mathrm{\pi }-0.24\mathrm{\pi }=3.51\mathrm{\pi }$

30) هندسة صناعية: صمم مهندس صناعي عجلة بكرة عن طريق تدوير جزء من منحنى الاقتران: $y=x^2+3$، يقع بين x=-1 و x=1 حول المحور x. أجد حجم عجلة البكرة.

$v={\int }_{-1}^1{\mathrm{\pi y}}^2 \mathrm{dx}={\int }_{-1}^1\mathrm{\pi }{({\mathrm{x}}^2+3)}^2\mathrm{dx}={\int }_{-1}^1\mathrm{\pi }({\mathrm{x}}^4+6{\mathrm{x}}^2+9) \mathrm{dx}=\mathrm{\pi }(\frac{1}{5}{\mathrm{x}}^5+2{\mathrm{x}}^3+9\mathrm{x}){|}_{-1}^{ 1}=\left(\frac{56}{5}\mathrm{\pi }\right)-(-\frac{56}{5}\mathrm{\pi })=\frac{112}{5}\mathrm{\pi }$

31) كرة قدم أمريكية: اذا دار منحنى المعادلة: $\frac{x^2}{{15}^2}+\frac{y^2}{{10}^2}=1$ حول المحور x، فان الشكل الناتج يشبه كرة القدم الأمريكية. أجد حجم الكرة الناتجة من دوران منحنى المعادلة السابقة حول محور x بالسنتيمترات المكعبة، مقربا اجابتي الى أقرب 3 منازل عشرية.

$v={\int }_{-15}^{15}{\mathrm{\pi y}}^2 \mathrm{dx}={\int }_{-15}^{15}\mathrm{\pi }(100-\frac{4}{9}{\mathrm{x}}^2) \mathrm{dx}=100\mathrm{\pi x}-\frac{4}{27}{\mathrm{\pi x}}^3{|}_{-15}^{ 15}=\left(1000\mathrm{\pi }\right)-(-1000\mathrm{\pi })=2000\mathrm{\pi }=6283.185$

مهارات التفكير العليا

32) تحد: يبين الشكل المجاور منحنيي الاقترانين: $f\left(x\right)={(x-2)}^2$ و $g\left(x\right)=(x-10)(2-x)$. أجد مساحة المنطقة المظللة R المحدودة بمنحنيي الاقترانين والمحور x.

$$\begin{gathered} f\left(x\right)=g\left(x\right) \\ {(x-2)}^2=(x-10)(2-x) \\ {x}^2-8x+12=0 \\ (x-2)(x-6)=0 \\ x=2 or x=6 \\ A={\int }_2^{6}f\left(x\right) dx+{\int }_6^{10}g\left(x\right) dx={\int }_2^6{(x-2)}^2 dx+{\int }_6^{10}(-x^2+12x-20) dx=\frac{1}{3}{(x-2)}^3{|}_2^6-\frac{1}{3}{x}^3+6x^2-20x{|}_6^{10}=64 \end{gathered}$$

33) تبرير: يبين الشكل المجاور دائرة معادلتها: $x^2+y^2=25$. اذا دار الجزء المظلل المحصور بين الدائرة والمستقيم y=4 حول المحور x لتشكيل مجسم، فأصف شكل المجسم الناتج، ثم أجد حجمه، مبررا اجابتي.

$$\begin{gathered} x^2+{\left(4\right)}^2=25 \\ x=\pm 3 \\ v={\int }_{-3}^3{\mathrm{\pi y}}^2 \mathrm{dx}={\int }_4^5\mathrm{\pi }(25-{\mathrm{x}}^2) \mathrm{dx}=\mathrm{\pi }(25\mathrm{x}-\frac{1}{3}{\mathrm{x}}^3){|}_{-3}^{ 3}=\mathrm{\pi }(75-9)-(-75+9)=132\mathrm{\pi } \end{gathered}$$

34) تحد: اذا كان ميل العمودي على المماس لمنحنى الاقتران f(x) عند النقطة (x,y) هو: $\frac{3}{x^2-6}$، ومر النحنى بنقطة الاصل، فأجد مساحة المنطقة المحصورة بين منحنى الاقتران f(x)، والمحور x، والمستقيمين x=1 و x=2.

$$\begin{gathered} m=\frac{3}{x^2-6} \\ f\text{'}\left(x\right)=\frac{6-x^2}{3} \\ f\left(x\right)=\int (2-\frac{1}{3}{x}^2) dx=2x-\frac{1}{9}{x}^3+C \\ f\left(0\right)=0 \\ f\left(x\right)=2x-\frac{1}{9}{x}^3 \\ f\left(x\right)=0 \\ 2x-\frac{1}{9}{x}^3=0 \\ x(2-\frac{1}{9}{x}^2)=0 \\ x=0 or x=\pm 3\sqrt{2} \\ A={\int }_1^2(2x-\frac{1}{9}{x}^3) dx=x^2-\frac{1}{36}{x}^4{|}_1^2=\frac{31}{12} \end{gathered}$$

حل أسئلة كتاب التمارين

أجد كلا من التكاملات الاتية:

$1) {\int }_1^3(3x^2+7) dx$

$40$

$2) {\int }_1^2(4x^3-1) dx$

$14$

$3) {\int }_1^8(\sqrt[3]{x}-2) dx$

$\frac{-11}{4}$

$4) {\int }_a^b\frac{1}{2}{x}^2 dx$

$\frac{b^3-a^3}{6}$

$5) {\int }_0^{27}\sqrt{3x} dx$

$162$

$6) {\int }_{-2}^5(2x^2-3x+7) dx$

$\frac{637}{6}$

7) أجد مساحة المنطقة المحصورة بين منحنيي الاقترانين: $f\left(x\right)=4x-x^2$، والمحور x.

وحدة مربعة${\int }_0^{4}4x-x^2=\frac{32}{3}$

8) أجد مساحة المنطقة المحصورة بين منحنيي الاقترانين: $f\left(x\right)=x^2+1$، والمحور x.

وحدة مربعة${\int }_{-2}^3{x}^2+1 dx=\frac{50}{3}$

9) أجد مساحة المنطقة المحصورة بين منحنى الاقتران: $f\left(x\right)=x^3-5x^2+6x$، والمحور x.

وحدة مربعة${\int }_0^2{x}^3-5x^2+6x dx-{\int }_2^3{x}^3-5x^2+6x dx=\frac{8}{3}+\frac{15}{12}=\frac{37}{12}$

10) يبين الشكل المجاور منحنى الاقتران $f\left(x\right)=\sqrt{x} , x>0$، اذا علمت أن النقطة P تقع على منحنى الاقتران، فأثبت أن مساحة المنطقة OPA المحصورة بين منحنى الاقتران f(x) والمحور x تساوي ثلثي مساحة المستطيل OAPB.

مساحة المنطقة OPA

${\int }_0^A\sqrt{x} dx={\int }_0^A{x}^{\frac{1}{2}}=\frac{2}{3}{x}^{\frac{3}{2}}{|}_0^A=\frac{2}{3}\sqrt{A^3}$

مساحة المستطيل

$(B-0)\times (A-0)=A\left(B\right)=A\left(P\right)=A\left(\sqrt{A}\right)=A^{\frac{3}{2}}=\sqrt{A^3}$

مساحة المنطقةOPAتساوي $\frac{2}{3}$ مساحة المستطيل

 

يبن الشكل المجاور منحنيي الاقترانين: $f\left(x\right)=\frac{1}{2}{x}^3$، و $g\left(x\right)={(x-4)}^2$:

11) أثبت أن منحنيي الاقترانين يتقاطعان في النقطة (2,4).

$$\begin{gathered} f\left(x\right)=g\left(x\right) \\ {(x-4)}^2=\frac{1}{2}{x}^3 \\ {x}^2-8x+16=\frac{1}{2}{x}^3 \\ {x}^3-2x^2+16x-32=0 \\ (x-2)(x+16)=0 \\ x-2=0 \\ x=2 \\ g\left(2\right)={(2-4)}^2=4 \end{gathered}$$

أو                      

$f\left(2\right)=\frac{1}{2}{\left(2\right)}^3=4$

نقطة التقاطع هي$(2,4)$

12) أجد حجم المجسم الناتج من دوران المنطقة المظللة حول المحور x.

وحدة مربعة$v={\int }_0^2{\left(\frac{1}{2}{x}^3\right)}^2 dx+{\int }_2^4({(x-4)}^2{)}^2 dx=\frac{384}{35}\mathrm{\pi }$

يبين الشكل المجاور منحنيي الاقترانين: $f\left(x\right)=x^2+14$، و $g\left(x\right)=x^4+2$:

13) اذا كان منحنيي الاقترانين يتقاطعان في النقطة: A و B، فأجد احداثيي نقطتي التقاطع.

$A(-2,18) B(2,18)$

14) أجد حجم المجسم الناتج من دوران المنطقة المظللة حول المحور x.

$$\begin{gathered} v={\int }_0^2\mathrm{\pi }\left({\mathrm{f}}^2\right(\mathrm{x})-{\mathrm{g}}^2(\mathrm{x}\left)\right) dx \\ ={\int }_0^2\mathrm{\pi }({({\mathrm{x}}^2+14)}^2-{({\mathrm{x}}^4+2)}^2) dx ={\int }_0^2\mathrm{\pi }({\mathrm{x}}^4+28{\mathrm{x}}^2+196-{\mathrm{x}}^8-4{\mathrm{x}}^4-4) dx \\ ={\int }_0^2\mathrm{\pi }(-{\mathrm{x}}^8-3{\mathrm{x}}^4+28{\mathrm{x}}^2+192) dx \\ =\mathrm{\pi }(-\frac{1}{9}{\mathrm{x}}^9-\frac{3}{5}{\mathrm{x}}^5+\frac{28}{3}{\mathrm{x}}^3+192\mathrm{x}) {|}_0^2 \end{gathered}$$

وحدة مكعبة$=\frac{3632\mathrm{\pi }}{9}$