الرياضيات فصل ثاني

الدرس الأول: التكامل غير المحدود : صفحة (8-14)

 

مسألة اليوم صفحة 8:

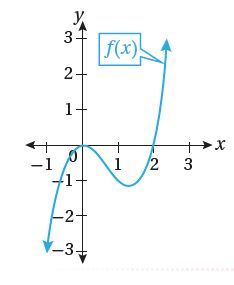
يبين الشكل المجاور منحنى الاقتران $f\left(x\right)$ ، هل يمكنني تحديد قاعدة الاقتران              

إذا علمت أن مشتقته هي: $f \mathit{َ}\left(x\right) = 3 x^2 - 4x$

                                                                

الـحـل :

نعم، بإيجاد تكامل المشتقة $\int f َ \left(x\right) dx = f\left(x\right)$ ، حيث:

 

               $$\begin{gathered} \int \left(3x^2 - 4x\right) dx = \int 3x^2 dx - \int 4x dx \\ = 3\mathbf{\int } x^2 dx - 4\int x dx \\ =3 \left(\frac{1}{3}{x}^3 \right) - 4\left(\frac{1}{2}{x}^2\right)+C \\ =x^3 - 2x^2 + C \end{gathered}$$

 

يمكن تحديد جذور الاقتران $f\left(x\right)$ من الشكل ، وهي: $(0, 0) , ( 2, 0)$

ويمكن تعويض الجذور بالاقتران $f\left(x\right)$  لإيجاد قيمة الثابت C

                             $$\begin{gathered} f\left(x\right)=x^3 - 2x^2 + C \\ f\left(0\right) = 0 - 2\left(0\right) + C \\ 0 = C \end{gathered}$$

 

إذن قاعدة الاقتران هي:  $f\left(x\right)=x^3 - 2x^2$

---

أتحقق من فهمي صفحة 9:

أجد اقترانًا أصليًا لكل من الاقترانين الآتيين:

                                  $$\begin{gathered} a) f(x) = 5x^4 \\ b) f\left(x\right)= -9 x^{-10} \end{gathered}$$

 

الـحـل :

a) الاقتران الأصلي للاقتران $f\left(x\right) = 5x^4$ هو: $F\left(x\right) = x^5 + C$ ، وذلك باتباع الخطوات الآتية:

$f\left(x\right) = 5x^4$	مشتقة الاقتران الأصلي
$F\left(x\right) = x^5$	بجعل أس x في الاقتران الأصلي أكثر بـــ 1 من أس x  في مشتقة اقتران القوة. حيث مشتقة $x^5$ هي  $5x^4$
$F\left(x\right) = x^5 + C$	أضف الثابت C للحصول على الاقتران الأصلي

          

 

 

 

 

 

 

 

 

 

 

 

 

 

b) الاقتران الأصلي للاقتران $f\left(x\right)= -9 x^{-10}$ هو:$F\left(x\right)= x^{-9} + C$  ، وذلك باتباع الخطوات الآتية:

$f\left(x\right)= -9x^{-10}$	مشتقة الاقتران الأصلي
$F\left(x\right)= x^{-9}$	بجعل أس x في الاقتران الأصلي أكثر بـــ 1 من أس x  في مشتقة اقتران القوة. حيث مشتقة $x^{-9}$  هي $-9x^{-10}$
$F\left(x\right)= x^{-9} + C$	أضف الثابت C للحصول على الاقتران الأصلي

                

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

     

أتحقق من فهمي صفحة 11:

أجد كلًا من التكاملات الآتية:

                  $\int 6 dx$ $\mathit{a}\mathbf{)}$                 
$\mathit{b}\mathbf{)}\mathbf{ }\mathbf{ }\int x^8 dx$
$\mathit{c}\mathbf{)} \int \sqrt[3]{x} dx$ 

$d) \int \frac{1}{x^5} dx$

الـحـل :

 

الاقتران	التكامل
$\mathit{a}\mathbf{)}\mathbf{ }\int 6 dx\mathbf{ }$	$\int 6 dx =6x + C$
$\mathit{b}\mathbf{)}\mathbf{ }\int x^8 dx$	$\int x^8 dx == \frac{1}{9} x^9 +C$
$\mathit{c}\mathbf{)}\mathbf{ }\int \mathbf{ }\sqrt[3]{x} dx$	$$\begin{gathered} \int \mathbf{ }\sqrt[3]{x} dx =\int \mathbf{ }{x}^{\frac{1}{3}} dx \\ =\frac{1}{\frac{1}{3}+1}{x}^{\frac{1}{3}+1} +C \\ = \frac{3}{4} x^{\frac{4}{3}} + C \\ =\frac{3}{4} \sqrt[3]{x^4} + C \end{gathered}$$
$\mathit{d}\mathbf{)}\mathbf{ }\int \frac{1}{x^5}dx$	$$\begin{gathered} \int \frac{1}{x^5}dx =\int x^{-5} dx \\ =\frac{1}{-5+1}\mathbf{ }{x}^{-5+1} +C \\ =\mathbf{ }\frac{1}{-4}\mathbf{ }{x}^{-4} +C \\ =\mathbf{ }\mathbf{-}\mathbf{ }\frac{1}{4 x^4}\mathbf{ } +C \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

أتحقق من فهمي صفحة 12:

أجد كلًا من التكاملين الآتيين:

      $$\begin{gathered} a)\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ }\left(x^3 -2 x^{\frac{5}{3}}\right) dx \\ b)\mathbf{ }\mathbf{ }\int (3x^2-\frac{6}{\sqrt[5]{x}}) dx \end{gathered}$$

الـحـل :

a) تكامل الاقتران $\mathbf{ }\left(x^3 -2 x^{\frac{5}{3}}\right)$ هو:

$\int \left(x^3 -2 x^{\frac{5}{3}} \right)dx = \int x^3 dx - \int 2x^{\frac{5}{3}} dx$	قاعدة تكامل الفرق
$= \int x^3 dx - 2\int x^{\frac{5}{3}} dx$	قاعدة تكامل الاقتران المضروب في ثابت
$= \left(\frac{1}{4}{x}^4\right) - 2\left(\frac{1}{\frac{8}{3}}{x}^{\frac{8}{3}}\right) + C$	قاعدة تكامل اقتران القوة
$= \frac{1}{4}{x}^4 - 2(\frac{3}{8} \sqrt[3]{x^8}) + C$	بكتابة الصورة الجذرية والتبسيط
$= \frac{1}{4}{x}^4 - \frac{3}{4} \sqrt[3]{x^8} + C$	بالتبسيط

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b) تكامل الاقتران $(3x^2-\frac{6}{\sqrt[5]{x}})$ هو:

$\int (3x^2-\frac{6}{\sqrt[5]{x}}) dx = \int 3x^2 dx - \int \frac{6}{x^{\frac{1}{5}}} dx$	قاعدة تكامل الفرق وتحويل الصورة الجذرية إلى أسية
$=3 \int x^2 dx - 6\int x^{-\frac{1}{5}} dx$	قاعدة تكامل الاقتران المضروب في ثابت وتعريف الأس السالب
$=3 (\frac{1}{3}{x}^3 ) - 6(\frac{1}{\frac{4}{5}}{x}^{\frac{4}{5}} ) + C$	قاعدة تكامل اقتران القوة
$$\begin{gathered} = x^3 - 6(\frac{5}{4}{x}^{\frac{4}{5}} ) + C \\ = x^3 - 3(\frac{5}{2}\sqrt[5]{x^4} ) + C \end{gathered}$$	بالتبسيط و كتابة الصورة الجذرية
$= x^3 -\frac{15}{2}\sqrt[5]{x^4} + C$	بالتبسيط

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

أتحقق من فهمي صفحة 13:

أجد كلًا من التكاملات الآتية:

$$\begin{gathered} a)\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ }\frac{x^4 -8 x^3}{x^2} dx \\ b)\mathbf{ }\mathbf{ }\mathbf{\int }(3x+2)\left(x-1\right) dx \\ c)\mathbf{ }\mathbf{ }\int x(x^3-7) dx \end{gathered}$$   

   

الـحـل :

a) تكامل الاقتران $\frac{x^4 -8 x^3}{x^2}$ هو: 

$\mathbf{\int }\mathbf{ }\frac{x^4 -8 x^3}{x^2} dx =\mathbf{\int }\mathbf{ }(\frac{x^4 }{x^2}-\frac{8 x^3}{x^2}) dx$	بقسمة كل حد في البسط على المقام
$=\mathbf{\int }\mathbf{ }(x^2-8x) dx$	بالتبسيط
$=\mathbf{\int }\mathbf{ }{x}^2 dx-\mathbf{\int } 8x dx$	تكامل الفرق
$$\begin{gathered} = \frac{x^3}{3}-\frac{8x^2}{2}+C \\ =\frac{1}{3}{x}^3 - 4x^2 +C \end{gathered}$$	تكامل اقتران القوة المضروب بثابت

  

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b) تكامل الاقتران $(3x+2)(x-1)$ هو: 

$\mathbf{\int }(3x+2)(x-1) dx =\mathbf{\int }(3x^2-3x+2x-2) dx$	بضرب المقدارين الجبريين
$=\mathbf{\int }(3x^2-x-2) dx$	بالتبسيط
$=\mathbf{\int }3x^2 dx-\int xdx-\int 2dx$	تكامل الفرق
$=\frac{3x^3}{3} -\frac{x^2}{2}-2x + C$	تكامل اقتران القوة المضروب بثابت وتكامل الثابت
$=x^3 -\frac{1}{2}{x}^2-2x +C$	بالتبسيط

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c) تكامل الاقتران $x(x^3-7)$ هو:

$\int x(x^3-7) dx=\int x^4-7x dx$	بتوزيع الضرب على الجمع
$=\int x^4 dx-\int 7x dx$	تكامل الفرق
$$\begin{gathered} =\frac{x^5}{5}-\frac{7x^2}{2}+C \\ =\frac{1}{5}{x}^5 -\frac{7}{2}{x}^{2 }+C \end{gathered}$$	تكامل اقتران القوة المضروب بثابت وتكامل الثابت

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

 

أتدرب وأحل المسائل صفحة 14:

 

أجد اقترانًا أصليًا لكل من الاقترانات الآتية:

                                     $$\begin{gathered} 1) f(x) = x^7 \\ 2) f(x) =-2 x^6 \\ 3) f(x) =-10 \\ 4) f(x) =8x \end{gathered}$$

 

الـحـل :

 

1) الاقتران الأصلي للاقتران $f\left(x\right) = x^7$  هو:$F\left(x\right) =\frac{1}{8} x^8 + C$ ، وذلك باتباع الخطوات الآتية: 

$f\left(x\right) = x^7$	مشتقة الاقتران الأصلي
$F\left(x\right) = x^8$	بجعل أس  $x$ في الاقتران الأصلي أكثر بـــ 1 من أس $x$ في المشتقة.
$F\left(x\right) =\frac{1}{8} x^8$	بضرب الاقتران بـــ $\left(\frac{1}{8}\right)$ لأن   مشتقة $x^8$ هي $\left(8 x^7\right)$ والعدد 8 غير مُعطى بمشتقة الاقتران بالسؤال ؛ فيجب التخلص من العدد 8 بالضرب بمقلوبه.
$F\left(x\right) =\frac{1}{8} x^8 + C$	أضف الثابت C للحصول على الاقتران الأصلي

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2) الاقتران الأصلي للاقتران $f\left(x\right) =-2 x^6$ هو:$F\left(x\right) =\frac{-2}{7} x^7 + C$ ، وذلك باتباع الخطوات الآتية:

$f\left(x\right) =-2 x^6$	مشتقة الاقتران الأصلي
$F\left(x\right) =-2 x^7$	بجعل أس x في الاقتران الأصلي أكثر بـــ 1 من أس x في المشتقة.
$F\left(x\right) =\frac{-2}{7} x^7$	بضرب الاقتران بـــ $\left(\frac{1}{7}\right)$ لأن مشتقة $x^7$ هي $(7 x^6)$ ، والعدد 7 غير مُعطى بمشتقة الاقتران بالسؤال ؛ فيجب التخلص من العدد 7 بالضرب بمقلوبه، مع الإبقاء على (2-)كما هي.
$F\left(x\right) =\frac{-2}{7} x^7 + C$	أضف الثابت C للحصول على الاقتران الأصلي

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3) الاقتران الأصلي للاقتران $f\left(x\right) =-10$ هو:$F\left(x\right) = -10 x + C$ ،  وذلك باتباع الخطوات الآتية:

 

$f\left(x\right) =-10$	مشتقة الاقتران الأصلي
$F\left(x\right) = -10 x^1$	بجعل أس x في الاقتران الأصلي $f\left(x\right) = -10 x^0$ أكثر بـــ 1 من أس x في المشتقة. حيث مشتقة $\left(-10 x\right)$ هي $\left(-10\right)$
$F\left(x\right) = -10 x + C$	أضف الثابت C للحصول على الاقتران الأصلي

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4) الاقتران الأصلي للاقتران $f\left(x\right) =8x$ هو:$F\left(x\right) =4x^2 + C$ ، وذلك باتباع الخطوات الآتية:

$f\left(x\right) =8x$	مشتقة الاقتران الأصلي
$F\left(x\right) =8x^2$	بجعل أس x في الاقتران الأصلي  أكثر بـــ 1 من أس x في المشتقة. حيث مشتقة $\left(x^2\right)$ هي $\left(2 x\right)$
$F\left(x\right) =\frac{1}{2}\left(8x^2\right) =4x^2$	بضرب الاقتران بـــ $\left(\frac{1}{2}\right)$
$F\left(x\right) =4x^2 + C$	أضف الثابت C للحصول على الاقتران الأصلي

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

 

 

أجد كلًا من التكاملات الآتية:

الســــــــــــــــــؤال	التكاملات
$\mathbf{5}\mathbf{)} \int 6x dx$	$$\begin{gathered} \int 6x dx =6 \frac{x^2}{2}+ C \\ = 3 x^2 + C \end{gathered}$$
$\mathbf{6}\mathbf{)} \mathbf{\int } \left(7x-5\right) dx$	$$\begin{gathered} \mathbf{\int }(7x-5) dx = \mathbf{\int }7x dx-\mathbf{\int }5 dx \\ =\frac{7}{2} x^2 - 5x +C \end{gathered}$$
$\mathbf{7}\mathbf{)} \mathbf{\int } (3 -4x) dx$	$$\begin{gathered} \int (3 -4x) dx=\mathbf{\int }3 dx -\mathbf{\int } 4x dx \\ = 3x -4 \frac{x^2}{2} +C \\ = 3x -2x^{2 } +C \end{gathered}$$
$\mathbf{8}\mathbf{)}\mathbf{ }\mathbf{\int }\frac{10}{\sqrt{x}}dx$	$$\begin{gathered} \mathbf{\int }\frac{10}{\sqrt{x}}dx=\mathbf{\int } 10 {\left(x\right)}^{-\frac{1}{2}} dx \\ = 10 ( \frac{1}{\frac{1}{2}} x^{\frac{1}{2}}) +C \\ = 20 \sqrt{x} +C \end{gathered}$$
$\mathbf{9}\mathbf{)}\mathbf{ }\mathbf{\int }\mathbf{ }2 x^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} dx$	$$\begin{gathered} \mathbf{\int }\mathbf{ }2 x^{\frac{3}{2}} dx = 2 (\frac{1}{\frac{5}{2}} x^{\frac{5}{2}})+C \\ = \frac{4}{5} x^{\frac{5}{2}} +C \\ =\frac{4}{5}\sqrt{x^5} +C \end{gathered}$$
$\mathbf{10}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{\int }(2 x^4 - 5 x + 10) dx$	$$\begin{gathered} \mathbf{\int }(2 x^4 - 5 x + 10) dx =\int 2 x^4 dx -\mathbf{\int } 5x dx + \mathbf{\int } 10 dx \\ =2\frac{ x^5}{5} - 5 \frac{x^2}{2} + 10 x + C \\ =\frac{2}{5} x^5 - \frac{5}{2} x^2 + 10 x + C \end{gathered}$$
$\mathbf{11}\mathbf{)}\mathbf{ }\mathbf{\int }\mathbf{ }(2 x^3 - 2 x ) dx$	$$\begin{gathered} \int \mathbf{ }(2 x^3 - 2 x ) dx =\int 2x^3 dx -\int 2x dx \\ = 2 \left(\frac{x^4}{4}\right) - 2 \left(\frac{x^2}{2}\right) + C \\ = \frac{1}{2} x^4 - x^2 + C \end{gathered}$$
$\mathbf{12}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ }(\frac{3}{\sqrt[3]{x}}-\sqrt{x^3}) dx$	$$\begin{gathered} \mathbf{ }\int (\frac{3}{\sqrt[3]{x}}-\sqrt{x^3}) dx = \mathbf{\int }\frac{3}{\sqrt[3]{x}}dx - \mathbf{\int } \sqrt{x^3} dx \\ = 3 \mathbf{\int } x^{-\frac{1}{3}} dx- \mathbf{\int } x^{\frac{3}{2}} dx \\ = 3 \left(\frac{1}{\frac{2}{3}} x^{\frac{2}{3}}\right) - \frac{1}{\frac{5}{2}} x^{\frac{5}{2}} + C \\ = \frac{9}{2} \sqrt[3]{x^2} - \frac{2}{5} \sqrt{x^5} + C \end{gathered}$$
$\mathbf{13}\mathbf{)} \int \left(\frac{1}{x^2}- \frac{1}{x^3}\right) dx$	$$\begin{gathered} \mathbf{\int }\left(\frac{1}{x^2}- \frac{1}{x^3}\right) dx = \mathbf{\int }\frac{1}{x^2} dx - \mathbf{\int }\frac{1}{x^3} dx \\ = \mathbf{\int } x^{-2} dx - \mathbf{\int } x^{-3} dx \\ = \frac{x^{-1}}{-1} - \frac{x^{-2}}{-2}+C \\ = -\frac{1}{x}+ \frac{1}{2x^2} +C \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

أجد كلًا من التكاملات الآتية:

الســــــــــــــــــؤال	التكاملات
$\mathbf{14}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{\int }\frac{4x^3 -2 }{x^3} dx$	$$\begin{gathered} \mathbf{\int }\frac{4x^3 -2 }{x^3} dx= \int \frac{4x^3}{x^3}dx -\int \frac{2}{x^3} dx \\ = \int 4 dx - \int 2 x^{-3} dx \\ = 4x - 2 \left(\frac{x^{-2}}{-2}\right) + C \\ = 4x + x^{-2} + C \\ = 4x + \frac{1}{x^2} + C \end{gathered}$$
$\mathbf{15}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\frac{2x +8}{\sqrt{x}} dx$	$$\begin{gathered} \int \frac{2x +8}{\sqrt{x}} dx =\mathbf{\int }\frac{2x}{\sqrt{x}}dx +\mathbf{\int } \frac{8}{\sqrt{x}}dx \\ = \mathbf{\int } \left(2x\right)\left(x^{-\frac{1}{2}}\right) dx + \int 8 x^{-\frac{1}{2}} dx \\ =2 \int x^{\frac{1}{2}} dx + 8 \int x^{-\frac{1}{2}} dx \\ = 2 \left(\frac{1}{\frac{3}{2}}{x}^{\frac{3}{2}}\right) + 8 \left(\frac{1}{\frac{1}{2}}{x}^{\frac{1}{2}}\right) + C \\ = \frac{4}{3}\sqrt{x^3} +16 \sqrt{x} + C \end{gathered}$$
$\mathbf{16}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ }{(x-1)}^2 dx$	$$\begin{gathered} \mathbf{\int }\mathbf{ }{(x-1)}^2 dx = \int \left(x^2-2x +1\right) dx \\ = \int x^2 dx -\int 2x dx + \int 1 dx \\ = \frac{x^3}{3}-\frac{2x^2}{2}+x +C \\ = \frac{1}{3}{x}^3-x^2+x +C \end{gathered}$$
$\mathbf{17}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{\int }\frac{x^3+8 }{x+2}dx$	$$\begin{gathered} \mathbf{\int }\frac{x^3+8 }{x+2}dx= \mathbf{\int } \frac{\left(x+2\right)\left(x^2-2x+4\right)}{x+2}dx \\ = \mathbf{\int }\mathbf{ }\left(x^2-2x+4\right) dx \\ = \mathbf{\int }{x}^2 dx - \mathbf{\int }2x dx + \mathbf{\int } 4 dx \\ = \frac{x^3}{3}- \frac{2x^2}{2}+ 4x + C \\ =\frac{1}{3}{x}^3 - x^2+ 4x + C \end{gathered}$$
$\mathbf{18}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ }\sqrt{x}(x-1) dx$	$$\begin{gathered} \mathbf{\int }\mathbf{ }\sqrt{x}(x-1) dx =\mathbf{\int }\mathbf{ }{x}^{\frac{1}{2}}(x-1) dx \\ = \mathbf{\int }\mathbf{ }(x^{\frac{3}{2}}- x^{\frac{1}{2}}) dx \\ = \mathbf{\int }\mathbf{ }{x}^{\frac{3}{2}} dx - \int x^{\frac{1}{2}} dx \\ = \frac{1}{\frac{5}{2}}{x}^{\frac{5}{2}} - \frac{1}{\frac{3}{2}}{x}^{\frac{3}{2}} +C \\ = \frac{2}{5}\sqrt{x^5} - \frac{2}{3}\sqrt{x^3} +C \end{gathered}$$
$\mathbf{19}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{\int }(2x-3\left)\right(3x-1) dx$	$$\begin{gathered} \mathbf{\int }(2x-3)(3x-1) dx = \int \left(6x^2-11x +3\right)dx \\ = \int 6x^2 dx-\int 11x dx +\int 3dx \\ = \frac{6x^3}{3}- \frac{11x^2}{2}+3x +C \\ = 2x^3-\frac{11}{2}{x}^2 +3x +C \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

مهارات التفكير العليا:

20) أكتشف الخطأ: أوجدت رنيم التكامل:$\int \left(2x + 1\right) \left(x-1\right) dx$ ، وكان حلها على النحو الآتي: 

         

$$\begin{gathered} \int (2x + 1) (x-1) dx = \int (2x + 1) dx \times \int (x-1) dx \\ = \left(x^2+x\right)\left(\frac{1}{2}{x}^2 -x\right)+C \end{gathered}$$

أكتشف الخطأ في حل رنيم، ثم أصححه.

 

 الحل:

الخطأ : التكامل لا يمكن توزيعه على عملية الضرب ، وإنما يجب إيجاد حاصل ضرب المقدارين أولًا ثم إيجاد التكامل.

 

الحل الصحيح:  

$$\begin{gathered} \int (2x + 1) (x-1) dx = \int (2x^2 -2x +x -1) dx \\ = \int (2x^2 -x -1) dx \end{gathered}$$	بضرب المقدارين الجبريين
$$\begin{gathered} = \int 2x^2 dx -\int x dx -\int 1 dx \\ = \frac{2x^3}{3}-\frac{x^2}{2}-x +C \\ =\frac{2}{3}{x}^3 -\frac{1}{2}{x}^2 -x +C \end{gathered}$$	تكامل اقتران القوة ، تكامل الثابت

 

 

 

 

 

 

 

 

 

 

 

 

 

---

 

تحدٍّ: أجد كل تكامل مما يأتي:

           $21)\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ }{\left(\frac{x^2 +1}{x^2}\right)}^2 dx 22)\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ }\left(x-1\right)\mathbf{ }\left(x-3\right)\left(x+5\right) dx$

الحل:

21) لإيجاد تكامل الاقتران ${\left(\frac{x^2 +1}{x^2}\right)}^2$ ، عليك اتباع الخطوات الآتية: 

 

$$\begin{gathered} \mathbf{\int }\mathbf{ }{\left(\frac{x^2 +1}{x^2}\right)}^2 dx =\int {\left(\frac{x^2}{x^2} + \frac{1}{x^2}\right)}^2 dx \\ = \int {\left(1 + \frac{1}{x^2}\right)}^{2 } dx \end{gathered}$$	قسمة كل حد في البسط على المقام
$= \int {\left(1 +\frac{2}{x^2} +\frac{1}{x^4}\right)}^{ } dx$	إيجاد مربع مجموع المقدارين ${\left(a+b\right)}^2 = a^2 +2ab + b^2$
$= \int 1 dx +\int 2x^{-2} dx {+\int x^{-4 }dx}^{ }$	تعريف الأس السالب، تكامل المجموع
$= x + \frac{2x^{-1}}{-1} {+ \frac{x^{-3 }}{-3}+ C}^{ }$	تكامل اقتران القوة ، تكامل الثابت
$= x -\frac{2}{x} -{\frac{1}{3x^3} + C}^{ }$	تعريف الأس السالب

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

22) لإيجاد تكامل حاصل ضرب الاقترانات $\left((x-1)\mathbf{ }(x-3)(x+5)\right)$ ، عليك ضربها أولًا ثم إيجاد التكامل كما يأتي:

$$\begin{gathered} (x-1)\mathbf{ }(x-3) =x^2 -3x -x +3 \\ =x^2 -4x +3 \\ \left(x^2 -4x +3\right)\left(x+5\right)=x^{3 }+5x^{2 }-4x^2 -20x +3x +15 \\ =x^{3 }+x^{2 } -17 x +15 \end{gathered}$$	بضرب المقادير الجبرية
$$\begin{gathered} \mathbf{\int }\mathbf{ }(x-1)\mathbf{ }(x-3)(x+5) dx=\int \left(x^{3 }+x^{2 } -17 x +15\right) dx \\ = \int x^3 dx +\int x^2 dx -\int 17 x dx +\int 15 dx \\ = \frac{1}{4}{x}^4+\frac{1}{3}{x}^3-\frac{17 }{2}{x}^2 + 15x + C \end{gathered}$$	حاصل ضرب المقادير الجبرية تكامل المجموع والفرق تكامل اقتران القوة ، تكامل الثابت

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

23)تبرير: إذا كان:$\int \left(\frac{P}{2 x^2}+ Q\right) dx = \frac{2}{x} + 10 x +C$ ، فأجد قيمة كل من الثابت$P$ ، والثابت $Q$، مبررًا إجابتي.

الحل:

لإيجاد الثوابت P , Q يمكنك البدء بالطرف الأيسر و إيجاد التكامل باتباع الخطوات الآتية:

 

$\int (\frac{P}{2 x^2}+ Q) dx =\int (\frac{P x^{-2}}{2}+ Q) dx$	تعريف الأس السالب
$$\begin{gathered} = \frac{P}{2}\left(\frac{x^{-1}}{-1}\right) + Q x + C \\ =\frac{-P}{2x} + Q x + C \end{gathered}$$	تكامل المجموع، تكامل اقتران القوة ، تكامل الثابت
$$\begin{gathered} \int (\frac{P}{2 x^2}+ Q) dx = \frac{2}{x} + 10 x +C \\ \frac{-P}{2x} + Q x + C = \frac{2}{x} + 10 x +C \end{gathered}$$	من المعطيات
$$\begin{gathered} \frac{-P}{2x}=\frac{2}{x}\to \frac{-P}{2}=2\to P=-4 \\ Q x =10 x \to Q=10 \end{gathered}$$	بما أن الطرف الأيمن يساوي الطرف الأيسر ، فإن كل حد يساوي الحد المقابل له، ومعاملات المتغيرات متساوية

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ملاحظة: يمكن البدء بالطرف الأيمن واستخدام المشتقة لإيجاد الثوابت.

 

---

 

كتاب التمارين صفحة 9:

 

أجد كلًا من التكاملات الآتية:

الســــــــــــــــــؤال	التكاملات
$\mathbf{1}\mathbf{)} \mathbf{\int } (4x+2) dx$	$$\begin{gathered} \mathbf{\int } (4x+2) dx = \mathbf{\int }4x dx+\mathbf{\int }2 dx \\ = \frac{4x^2}{2} + 2x +C \\ =2x^2 + 2x +C \end{gathered}$$
$\mathbf{2}\mathbf{)} \mathbf{\int } 2x^{-4} dx$	$$\begin{gathered} \mathbf{\int } 2x^{-4} dx=\frac{2 x^{-3}}{-3}+C \\ =-\frac{2}{3} x^{-3} +C \\ =-\frac{2}{3x^3} +C \end{gathered}$$
$\mathbf{3}\mathbf{)} \mathbf{\int } \left(6x^2 - 4x\right) dx$	$$\begin{gathered} \mathbf{\int } (6x^2 - 4x) dx= \frac{6x^3}{3} - \frac{4 x^2}{2} + C \\ = 2x^3 - 2x^{2 }+ C \end{gathered}$$
$\mathbf{4}\mathbf{)} \mathbf{\int } \left(3- x -2x^5 \right) dx$	$$\begin{gathered} \mathbf{\int }(3- x -2x^5 ) dx= 3x - \frac{x^2}{2}-\frac{2x^6}{6} +C \\ = 3x - \frac{1}{2}{x}^2- \frac{1}{3}{x}^6 +C \end{gathered}$$
$\mathbf{5}\mathbf{)} \mathbf{\int } \left(x^{-2}+ x^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} \right) dx$	$$\begin{gathered} \mathbf{\int } (x^{-2}+ x^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} ) dx = \frac{x^{-1}}{-1} + \frac{1}{\frac{7}{2}}{x}^{\frac{7}{2}} + C \\ = - x^{-1} + \frac{2}{7}{x}^{\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} + C \\ = -\frac{1}{x}+\frac{2}{7}\sqrt{x^7} + C \end{gathered}$$
$\mathbf{6}\mathbf{)} \mathbf{\int } \left(3x^2- \frac{2}{x^2} \right) dx$	$$\begin{gathered} \mathbf{\int } (3x^2- \frac{2}{x^2} ) dx=\mathbf{\int } (3x^2-2x^{-2} ) dx \\ = \frac{3x^3}{3}-\frac{2 x^{-1}}{-1}+C \\ = x^3 + 2 x^{-1 }+C \\ = x^3 + \frac{2}{x} +C \end{gathered}$$
$\mathbf{7}\mathbf{)} \mathbf{\int } \left(3x^{-2}+6 x^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} +x -4\right) dx$	$$\begin{gathered} \mathbf{\int } (3x^{-2}+6 x^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} +x -4) dx=\frac{3x^{-1}}{-1}+\frac{6x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\frac{1}{2}}+\frac{x^2}{2}-4x+C \\ = -3x^{-1 }+12 x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2 $}\right. }+\frac{1}{2}{x}^2 -4x +C \\ = -\frac{3}{x}+ 12 \sqrt{x} +\frac{1}{2}{x}^2 -4x +C \end{gathered}$$
$\mathbf{8}\mathbf{)} \mathbf{\int } \left(10x^4+8 x^{-3} \right) dx$	$$\begin{gathered} \mathbf{\int } (10x^4+8 x^{-3} ) dx = \frac{10 x^5}{5}+ \frac{8 x^{-2}}{-2} +C \\ = 2 x^5 -4 x^{-2} +C \\ = 2 x^5 -\frac{4}{x^2}+C \end{gathered}$$
$\mathbf{9}\mathbf{)} \mathbf{\int } \left(\frac{2}{x^3}- 3\sqrt{x} \right) dx$	$$\begin{gathered} \mathbf{\int } (\frac{2}{x^3}- 3\sqrt{x} ) dx = \int (2x^{-3} - 3 x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.})dx \\ = \frac{2 x^{-2}}{-2} - \frac{3 x^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\frac{3}{2}} + C \\ = - x^{-2} -2 x^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} + C \\ = -\frac{1}{x^2}-2 \sqrt{x^3} + C \end{gathered}$$
$\mathbf{10}\mathbf{)} \mathbf{\int } \left(8x^3+6x - \frac{4}{\sqrt{x}} \right) dx$	$$\begin{gathered} \mathbf{\int } (8x^3+6x - \frac{4}{\sqrt{x}} ) dx = \mathbf{\int } (8x^3+6x -4 x^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} ) dx \\ =\frac{8 x^4}{4} + \frac{6x^2}{2} - \frac{4 x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\frac{1}{2}}+ C \\ = 2 x^4 + 3 x^2 - 8 \sqrt{x} + C \end{gathered}$$
$\mathbf{11}\mathbf{)} \mathbf{\int } \left(\frac{7}{x^2}+ \sqrt[3]{x^4} \right) dx$	$$\begin{gathered} \mathbf{\int } (\frac{7}{x^2}+ \sqrt[3]{x^4} ) dx = \mathbf{\int } (7 x^{-2}+x^{\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.} ) dx \\ = \frac{7 x^{-1}}{-1} + \frac{x^{\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}{\frac{7}{3}} + C \\ = -\frac{7}{x} + \frac{3}{7} \sqrt[3]{x^7} + C \end{gathered}$$
$\mathbf{12}\mathbf{)} \mathbf{\int } \left(\frac{x^2}{3}+ \frac{3}{x^2} \right) dx$	$$\begin{gathered} \mathbf{\int } (\frac{x^2}{3}+ \frac{3}{x^2} ) dx = \mathbf{\int } (\frac{x^2}{3}+3 x^{-2} ) dx \\ = \frac{1}{3}\left(\frac{x^3}{3}\right) + 3 \left(\frac{x^{-1}}{-1}\right) + C \\ = \frac{1}{9}{x}^3 -\frac{3}{x} + C \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

أجد كلًا من التكاملات الآتية:

الســــــــــــــــــؤال	التكاملات
$\mathbf{13}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\frac{4+2\sqrt{x}}{x^2} dx$	$$\begin{gathered} \mathbf{\int }\frac{4+2\sqrt{x}}{x^2} dx =\int \frac{4}{x^2} dx+\int \frac{2\sqrt{x}}{x^2}dx \\ =\int 4 x^{-2} dx+\int 2 x^{\raisebox{1ex}{$-3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} dx \\ =\frac{4 x^{-1}}{-1} + \frac{2 x^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+C \\ = - \frac{4}{x} -\frac{4}{\sqrt{x}} + C \end{gathered}$$
$\mathbf{14}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\frac{4-x^2}{2+x} dx$	$$\begin{gathered} \mathbf{\int }\frac{4-x^2}{2+x} dx = \int \frac{(2-x)(2+x)}{2+x} dx \\ = \int (2-x) dx \\ = 2x - \frac{x^2}{2} + C \\ = 2x -\frac{1}{2}{x}^2 + C \end{gathered}$$
$\mathbf{15}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\frac{x^2 -1}{x^2} dx$	$$\begin{gathered} \mathbf{ }\mathbf{\int }\frac{x^2 -1}{x^2} dx =\int \frac{x^2}{x^2}dx -\int \frac{1}{x^2}dx \\ = \int 1 dx - \int x^{-2} dx \\ = x - \frac{x^{-1}}{-1} + C \\ = x + \frac{1}{x}+C \end{gathered}$$
$\mathbf{16}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ }x \sqrt{x} dx$	$$\begin{gathered} \mathbf{\int }\mathbf{ }x \sqrt{x} dx = \int x^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} dx \\ = \frac{x^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\frac{5}{2}}+ C \\ = \frac{2}{5}\sqrt{x^5 } + C \end{gathered}$$
$\mathbf{17}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ }\frac{x^2 - 1}{x-1} dx$	$$\begin{gathered} \mathbf{\int }\mathbf{ }\frac{x^2 - 1}{x-1} dx = \int \frac{\left(x-1\right)\left(x+1\right)}{x-1}dx \\ = \int \left(x + 1\right) dx \\ =\frac{1}{2}{x}^2 + x + C \end{gathered}$$
$\mathbf{18}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ }{x}^2 \left(1-x^3\right) dx$	$$\begin{gathered} \mathbf{\int }\mathbf{ }{x}^2 \left(1-x^3\right) dx =\int x^2 dx - \int x^5 dx \\ = \frac{1}{3}{x}^3- \frac{1}{6}{x}^6+C \end{gathered}$$
$\mathbf{19}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ } {\left(x+4\right)}^2 dx$	$$\begin{gathered} \mathbf{\int }\mathbf{ } {(x+4)}^2 dx =\int \left(x^2 +8x + 16\right)dx \\ = \frac{x^3}{3}+ \frac{8x^2}{2}+16 x + C \\ = \frac{1}{3}{x}^3 + 4 x^2 +16 x + C \end{gathered}$$
$\mathbf{20}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ } \frac{5-x}{x^5} dx$	$$\begin{gathered} \mathbf{\int }\mathbf{ } \frac{5-x}{x^5} dx =\int \frac{5}{x^5}dx - \int \frac{x}{x^5}dx \\ = \int 5 x^{-5} dx - \int x^{-4} dx \\ = \frac{5 x^{-4}}{-4} - \frac{x^{-3}}{-3}+C \\ = -\frac{5}{4 x^4} + \frac{1}{3 x^3}+ C \end{gathered}$$
$\mathbf{21}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ } \frac{x^2 + 2x +1}{x+1} dx$	$$\begin{gathered} \mathbf{\int }\mathbf{ } \frac{x^2 + 2x +1}{x+1} dx =\int \frac{\left(x+1\right)\left(x+1\right)}{x+1}dx \\ = \int \left(x+1\right)dx \\ = \frac{1}{2}{x}^2+ x+ C \end{gathered}$$
$\mathbf{22}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ } x {\left(x+1\right)}^2 dx$	$$\begin{gathered} \mathbf{ }\mathbf{\int }\mathbf{ } x {(x+1)}^2 dx =\int x\left(x^2 + 2x + 1\right) dx \\ = \int \left(x^3 + 2x^2 + x\right)dx \\ = \frac{1}{4}{x}^4+\frac{2 }{3}{x}^3+\frac{1}{2}{x}^2+C \end{gathered}$$
$\mathbf{23}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ } \frac{ {(x+3)}^2}{\sqrt{x}} dx$	$$\begin{gathered} \mathbf{\int }\mathbf{ } \frac{ {(x+3)}^2}{\sqrt{x}} dx =\int x^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} {\left(x+3\right)}^2 dx \\ =\int x^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} \left(x^2 + 6x + 9\right) dx \\ =\int x^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} dx +\int 6x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} dx + \int 9 x^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} dx \\ = \frac{x^{\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\frac{5}{2}}+ \frac{6 x^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\frac{3}{2}}+ \frac{9 x^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\frac{1}{2}}+ C \\ = \frac{2}{5}\sqrt{x^5} + 4 \sqrt{x^3} +18 \sqrt{x} + C \end{gathered}$$
$\mathbf{24}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\int }\mathbf{ } \left(x-5\right)\left(x+5\right) dx$	$$\begin{gathered} \mathbf{\int }\mathbf{ } \left(x-5\right)\left(x+5\right) dx =\int \left(x^2 - 25\right)dx \\ = \int x^2 dx - \int 25 dx \\ = \frac{1}{3}{x}^3-25 x+ C \end{gathered}$$