الرياضيات فصل ثاني

الدرس الرابع:التوزيع الطبيعي المعياري

Standard Normal

التوزيع الطبيعي المعياري

 

يسمى المُتغيَّر العشوائي الطبيعي الذي وسطه

الحسابي$0$ وانحرافه المعياري$1$بالتوزيع الطبيعي المعياري ويُعبر عنه بالرموز بالصورة الآتية:$Z~N(0, 1)$، ويُمثَّل منحناه بيانيًا بالشكل الآتي:

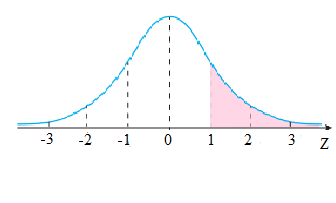
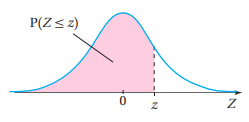
وفي الشكل تُمثل مساحة المنطقة المظللة احتمال قيم المتغير العشوائي الطبيعي المعياري$Z$التي تزيد عن القيمة المعيارية $Z=1$  وبالرموز : $P(Z>1)$ .

خصائص التوزيع الطبيعي المعياري

1) وسطه الحسابي $0$ وانحرافه المعياري $1$.

2) منحنى التوزيع الطبيعي المعياري متماثل حول الوسط الحسابي.

3) المساحة تحت منحنى التوزيع الطبيعي تساوي $1$ وحدة مربعة.

 

احتمال قِيَم المُتغيِّر العشوائي الطبيعي المعياري $Z$.

احتمال قِيَم المُتغيِّر العشوائي الطبيعي المعياري $Z$ التي تقل عن (أو تساوي)القيمة المعيارية $z$ هي: $P(Z\le z)$.

1) المساحة (الاحتمال) تحت القيمة المعيارية الموجبة من الجدول مباشرة 

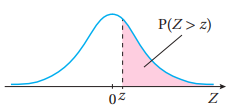
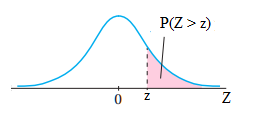
2) المساحة (الاحتمال) فوق القيمة المعيارية الموجبة

بالرموز:

$P(Z>z)=1-P(Z<z)$

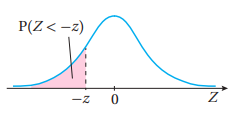
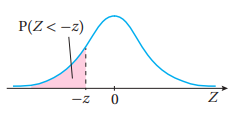
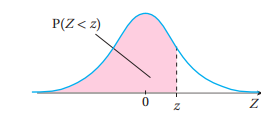
3) المساحة (الاحتمال) تحت القيمة المعيارية السالبة

المساحة (الاحتمال) تحت القيمة المعيارية السالبة = المساحة (الاحتمال) فوق القيمة المعيارية الموجبة

بالرموز:

 $P(Z<-z)=P(Z>z) =1-P(Z<z)$

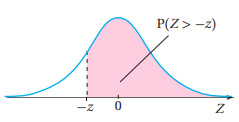
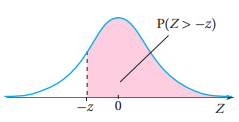
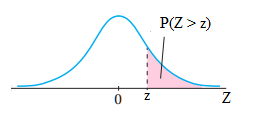
4) المساحة (الاحتمال) فوق القيمة المعيارية السالبة

        

المساحة (الاحتمال) فوق القيمة المعيارية السالبة = المساحة (الاحتمال) تحت القيمة المعيارية الموجبة

 

بالرموز: $P(Z>-z)=P(Z<z)$

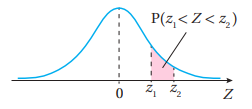
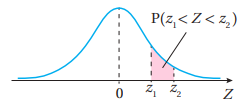
5) المساحة(احتمال) القيم التي تقع بين قيمتين معياريتين

احتمال القيم التي تقع بين قيمتين معياريتين = احتمال القيم التي تقع تحت القيمة المعيارية الكبرى -  احتمال القيم التي تقع تحت القيمة المعيارية الصغرى

بالرموز:

 $P(z_1<Z<z_2)=P(Z<z_2)-P(Z<z_1)$

ملخص المفهوم

إيجاد احتمال المُتغيِّر  العشوائي الطبيعي المعياري

إذا كان: $Z~N(0, 1)$، فإنَّ:

 $1) P(Z>z)=1-P(Z<z)$

$2) P(Z<-z)=1-P(Z<z)$

$3)P(Z>-z)=P(Z<z)$

$4) P(z_1<Z<z_2)= P(Z<z_2)-P(Z<z_1)$

إيجاد قيمة المُتغيِّر العشوائي إذا عُلِم الاحتمال ويتم من خلال القوانين والجدول المعطى.