الوحدة الثالثة
الأساس المنطقي للحاسوب والبوابات المنطقية
الفصل الثالث : الجبر المنطقي ( البوولي )
- يتكون الحاسوب من مكونات مادية مرتبطة معاً ( لتنفيذ مجموعة من الوظائف )
- يمكن تحديد وظائف المكونات المادية وتنفيذها من خلال فهم وظيفة كل جزء من المكونات المادية وفهم كيفية ارتباطه بالأجزاء الأخرى لتبادل المعلومات
- يمكن أن تحدّد الوظائف وعمليات الربط بين المكونات المادية لجهاز الحاسوب (من خلال نموذج رياضي حيث يمكن تمثيله بعلاقات منطقية أو جبرية )
من مسميات للجبر البوولي الجبر المنطقي ، عمليات الجبر المنطقي
أولاً : مفهوم الجبر البوولي ( المنطقي )
الجبر البوولي ( الجبر/ المنطقي ) : هو أحد فروع علم الجبر في الرياضات وهو الأساس الرياض اللازم لدراسة التصميم المنطقي للأنظمة الرقمية ومنها الحاسوب
تعود تسمية الجبر البوولي للعالم الانجليزي جورج بوول
من كُتب العالم جورج بوول في علم الجبر المنطقي ( البوولي )
1 - التحليل الرياضي للمنطق
2 - دراسة في قوانين التفكير وهو الذي قدّم به الجبر المنطقي بشكل واسع و أكّد فيه على أن استخدام الصيغة الجبرية في وصف عمل الحاسوب الداخلي أسهل من التعامل مع البوابات المنطقية
المتغير المنطقي هو المتغير الذي تعيّن له حالتين إما صواب أو خطأ
عند كتابة المتغير المنطقي يجب أن يرمز له بأحد الحروف A......Z
و لا أهمية للأحرف كبيرة أم صغيرة حيث تمثل قيمة المتغير المنطقي بــ ( 0 أو 1 ) فالرقم ( 1 ) يعبّر عنه بالحالة الصحيحة .........و الرقم ( 0 ) الحالة الخطأ
النظام الأنسب لتمثيل الأعداد والرموز وتخزينها داخل الحاسوب هو
نظام العد الثنائي ( 0 أو 1 )
ثانياً: العبارات الجبرية المنطقية والعمليات المنطقية
العبارة الجبرية المنطقية هي ثابت منطقي ( 0 ، 1 ) أو متغير منطقي مثل ( X ، Y) أو مزيج من الثوابت والمتغيرات المنطقية يجمع بينهما عمليات منطقية
ملاحظة : يمكن أن تحتوي العبارة الجبرية المنطقية على :
1- أقواس 2 - أكثر من عملية منطقية
العمليات المنطقية الأساسية في الجبر المنطقي ( البوولي )
أ - عملية NOT
يطلق عليها بالجبر البوولي ( المنطقي ) اسم المتمم لأن متممة 0 تساوي 1 و متممة 1 هي 0
العبارة الجبرية المنطقية لعملية NOT .
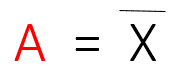
جدول الحقيقة للعبارة السابقة
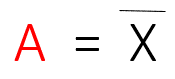 |
X |
| 0 | 1 |
| 1 | 0 |
تمثيل العبارة الجبرية السابقة بالبوابات المنطقية
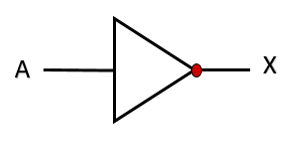
ب- عملية AND
يعبر عن عملية AND بالجبر البوولي ( المنطقي ) بالرمز ( . )
العبارة الجبرية المنطقية لعملية AND.
A = X . Y
جدول الحقيقة للعبارة الجبرية السابقة
| A = X . Y | Y | X |
| 1 | 1 | 1 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
تمثيل العبارة الجبرية السابقة بالبوابات المنطقية
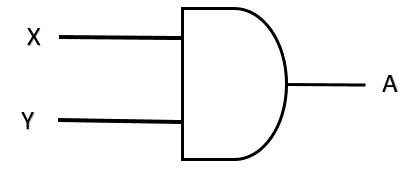
ج- عملية OR
يعبر عن عملية OR بالجبر المنطق ( البوولي ) بالرمز ( + )
العبارة الجبرية المنطقية لعملية OR .
A = X + Y
جدول الحقيقة للعبارة الجبرية السابقة
| A = X + Y | Y | X |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 0 | 0 | 0 |
تمثيل العبارة الجبرية السابقة بالبوابات المنطقية
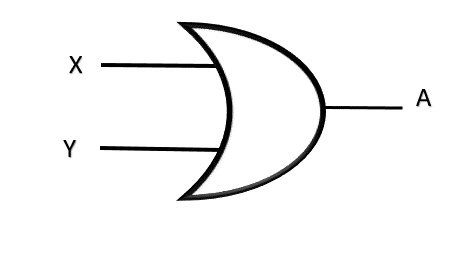
ثالثاً : ايجاد ناتج العبارة الجبرية المركبة
العبارة الجبرية المركبة :هي العبارة الجبرية التي تحوي اكثر من عملية منطقية أساسية
لايجاد ناتج عبارة جبرية منطقية مركبة نتبع الأولويات :
- الأقواس إن وجدت ( ) حيث تنفذ العمليات التي بداخلها أولاً
- البوابة المنطقية NOT
- البوابة المنطقية AND
- البوابة المنطقية OR
- في حالة تكافؤ وتساوي الأولويات تنفذ الاولويات من اليسار لليمين
مثال ( 1 ) جد ناتج العبارة الجبرية المنطقية
X = A . B + C . D
علما بأن A= 0 , B= 1 , C = 1 , D = 1
الحل : نتبع الخطوات التالية
1- نعوّض القيم فتصبح X = 0 . 1 + 1 . 1
2 - نتبع الأولويات كما يلي
X = 0 . 1 + 1 . 1
X = 0 + 1 . 1
X = 0 + 1
X = 1
رابعاً : تمثيل العبارات الجبرية المنطقية المركبة باستخدام البوابات المنطقة
عند تمثيل عبارة الجبرية المنطقية نتبع الأولويات في الرسم كما تم شرحه مسبقا
مثال مثل العبارة الجبرية المنطقية Z = A + B . C باستخدام البوابات المنطقية ثم جد قيمة Z اذا كانت
A = 1 , B = 1 , C = 0
خطوات الحل :
1 - عند التمثيل / الرسم نتبع الأولويات
فالأولوية لــ AND ( . )
Z = A + B . C
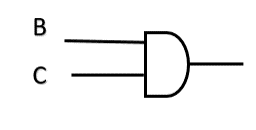
مخرج بوابة AND هي المدخل الاول لبوابة OR والمدخل الآخر هو A فتصبح
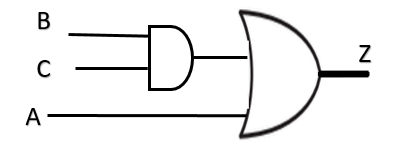
ثم نعوض على الرسمة قيم المتغيرات المنطقية و نجد الناتج كما في الشكل