حلول أسئلة كتاب الطالب وكتاب التمارين
حلول أسئلة أتحقق من فهمي
أتحقق من فهمي صفحة 15
أجد قيمة كل مما يأتي:
أتحقق من فهمي صفحة 16
أجد قيمة كل مما يأتي:
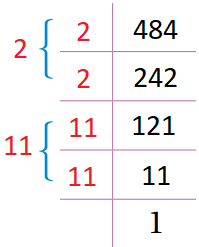 |
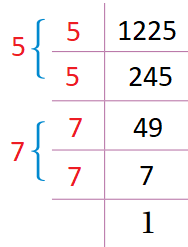 |
أتحقق من فهمي صفحة 17
أجد قيمة كل مما يأتي:
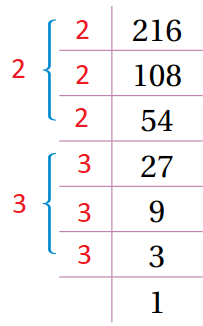 |
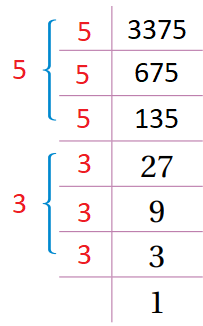 |
|
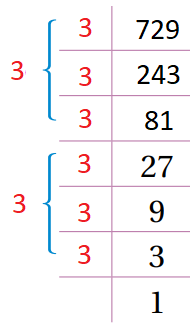
جد القيمة المطلقة للعدد 729- ، وهي 729 ، ثم حللها إلى عواملها الأولية:
ثم نحسب الجذر التكعيبي للعدد 729 بأخذ عامل من كل ثلاثة تكرارات له. وفي النهاية نضع الإشارة السالبة في الجواب. |
إذن؛ |
 |
أتحقق من فهمي صفحة 17
| مرور: تُرشد لوحة المُرور المُجاورة السّائقين إلى أنّ الطّريق يَضيق، وهي لوحة مُربعة الشكل، ومساحتُها، أجدُ طول ضلع هذه اللّوحة. |  |
الحل:
حلل العدد 4225 إلى عوامله الأولية
أحسب الجذر بأخذ عامل من كل تكرارين له
إذن، طول ضلع اللوحة 65 cm
حلول أسئلة أتدرب وأحل المسائل
أجد قيمة كل مما يأتي:
أجد قيمة كل مما يأتي:
13) مَدارس: ساحة مَدرسة هُدى مُربعة الشكل، مساحَتُها ، أجدُ طول ضِلعها.
الحل:
بما أنّ ساحة المدرسة مُربعة الشكل فإنّ طول ضِلعها يُساوي الجذر التربيعي لمساحتها.
|
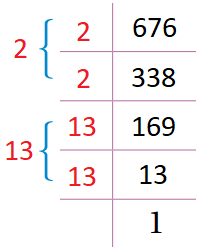
نحلل العدد 676 إلى عوامله الأولية ، ثم نأخذ عاملا من كل تكرارين له |
 |
|
فيكون الجذر التربيعي (طول الضلع) يساوي ناتج ضرب العوامل المُختارة. |
|
|
إذن، طول ضلع ساحة المدرسة 26 m |
|
| 14) أراضٍ: أرضٌ مُربعة الشّكل، مساحتُها ، يُريد بلال تحويطها بسياج من الأسلاك، أحسبُ طول السّياج اللازم لذلك. |  |
الحل:
بما أنّ الأرض مُربعة الشكل فإنّ طول ضلع السياح يُساوي الجذر التربيعي لمساحتها.
|
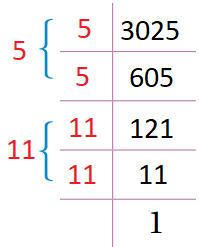
نحلل العدد 3025 إلى عوامله الأولية ، ثم نأخذ عاملا من كل تكرارين له |
 |
|
فيكون الجذر التربيعي (طول الضلع) يساوي ناتج ضرب العوامل المُختارة. |
|
|
إذن، طول ضلع السياج 55 m طول السياج= 4 × طول الضلع |
|
أجد قيمة كل مما يأتي ذهنيا:

أضَعُ (<) أو (>) أو (=) في لأُكوّن عبارة صحيحة في كل مما يأتي:
18)
19)
20) أعدادٌ: أجدُ عددًا جذرهُ التربيعي يُساوي جذْرهُ التّكعيبي.
الحل:
مثال: العدد (1)
العدد(0)
21) أعدادٌ: أجدُ ثلاثة أعداد قيمة كلّ منها يُساوي جَذرها التكعيبي.
الحل:
العدد (1) حيثُ أنّ:
العدد (1-) حيثُ أنّ:
العدد (0) حيثُ أنّ:
أجد قيمة كل مما يأتي:
22)
23)
24)
|
25) زِراعة: وَضعَ مُزارع العدد نَفسه من عِبوات الكرز في صناديق، إذا كان عدد العُبوات في الصّندوق الواحد يُساوي عدد الصّناديق جميعها، وكان مجموع العُبوات في الصناديق جميعِها 144 عبوة، فما عدد الصّناديق؟ |
 |
الحل:
عدد العبوات = عدد العبوات في الصندوق × عدد الصناديق
لكن عدد العبوات في الصندوق = عدد الصناديق ؛ أي أنّ:
144 = ×
الآن أبحث عن عدد إذا ضُرب في نفسه يُعطي 144 فيكون العدد هو 12
عدد الصناديق يساوي 12 وهو يمثل
حلول أسئلة مهارات التفكير العُليا
تحدٍّ: ما قيمة كلّ مما يأتي:
26)
27)
28)
29) تحدٍّ: ما أصغرُ عددٍ كُليّ عند ضربه في العدد (72) يكون النّاتج مُكعبا كاملاً؟ أجدُ الجذر التكعيبي للمكعّب الكامل النّاتج.
الحل:
العدد (3) ، حيثُ:
و 216 مُكعب كامل
30) أكْتشِفُ الخطأ: قال يوسف: إنّ .
أكتشف الخطأ في ما قاله، وأُصحّحُه.
الحل:
الخطأ: في ناتج الجذر التكعيبي حيثُ حسب يوسف الجذر التربيعي للعدد 64 وليس جذره التكعيبي.
الصواب:
31) أكتبُ: ما الفرق بين الجذر التّربيعي والجذر التّكعيبي؟
الحل:
الجذر التربيعي هو ذلك العدد الذي إذا ضرب في نفسه يُعطي المربع الكامل (ما بداخل الجذر).
والجذر التكعيبي هو ذلك العدد الذي إذا ضرب في نفسه ثلاث مرات يُعطي المُكعب الكامل (ما بداخل الجذر).
حلول أسئلة كتاب التمارين
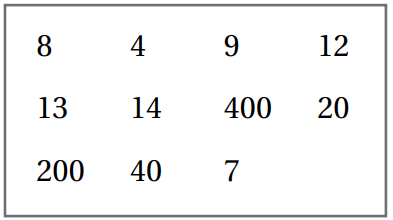
أختارُ من المُستطيل قيمة الجذر التّربيعي لكل مما يأتي:
 |
2) | 1) |
| 4) | 3) | |
| 6) | 5) |
أختارُ من المُستطيل قيمة الجذر التّكعيبي لكل مما يأتي:
| 7) | 8) | 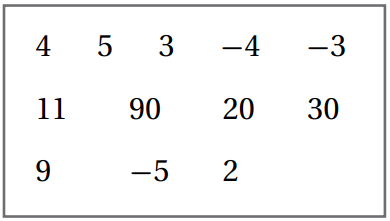 |
| 9) | 10) | |
| 11) | 12) |
أجد قيمة كل مما يأتي باستعمال التحليل إلى العوامل الأولية:
| 14) | 13) |
| 16) | 15) |
| 18) | 17) |
19) حَدائق: حديقة مُربّعة الشكل مساحتُها m2 4225 ، فما طول ضلعها؟
الحل:
بما أنّ الحديقة مُربعة الشكل فإنّ طول ضِلعها يُساوي الجذر التربيعي لمساحتها.
إذن، طول ضلع الحديقة 65 m
20) إذا كان و فما قيمة ؟
الحل:
عدد جذره التربيعي يساوي 12 هو 144
العدد هو 8
أكمل الفراغ بكتابة العدد الناقص في كل مما يأتي:
| 22) | 21) |
| 24) | 23) |
| 26) | 25) |
| 28) | 27) |