الفيزياء 11 فصل ثاني

 

 

 

يُعدّ البندول البسيط من الأمثلة العملية على الحركة التذبذبية ،مثل حركة الأرجوحة وحركة بندول الساعة.

 

 

يتكون البندول البسيط من جسم ذي كتلة صغيرة معلقة بخيط رفيع مهمل الكتلة مثبت على حامل .

كيف يتحرك البندول عند سحبه؟

 

 

ذهابًا وإيابًا حول موقع الاتزان.

عندما تترك الكرة فإنها تتذبذب على طول القوس الدائري وليس في خط مستقيم.

تحليل القوى في حركة البندول

 عند سحب الكرة كتلتها m  معلقة بحبل طوله  L نحو اليمين بحيث يمسح خط البندول زاوية $\mathit{\theta }$ وتقطع الكرة مسافة قوسية s عن موقع الاتزان . 

تؤثر في الكتلة قوى في المحور X والمحور y .

-قوة شد من الحبل على كتلة 

- قوة جذب الأرض للكتلة 

 

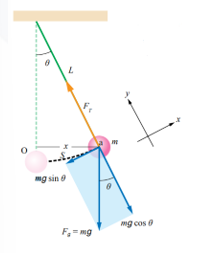
-على المحور الصادي 

$\mathbf{\sum }{\mathit{F}}_{\mathbf{y}}\mathbf{=}{\mathit{F}}_{\mathbf{T}}\mathbf{-}\mathit{m}\mathit{g}\mathbf{ }\mathit{c}\mathit{o}\mathit{s}\mathit{\theta }$

 

-على المحور السيني 

$\mathbf{\sum }{\mathit{F}}_{\mathbf{x}}\mathbf{=}\mathbf{-}\mathit{m}\mathit{g}\mathbf{ }\mathit{s}\mathit{i}\mathit{n}\mathit{\theta }$

 

تكون القوة على محور x هي المسؤولة عن اعادة الكرة الى موقع الاتزان وتسمى القوة المعيدة.

وهي مركبة القوة المحصلة باتجاه المماس.

 

 

 

 

اذا تحرك البندول بزاوية صغيرة جدًّا$\left(\theta \le 10\right)$ فإن $\mathit{s}\mathit{i}\mathit{n}\mathbf{ }\mathit{\theta }$ يساوي الزاوية $\theta$ .

 

 

 

وتكون القوة المعيدة

$\mathit{F}\mathbf{=}\mathbf{ }\mathbf{-}\mathit{m}\mathit{g}\mathbf{ }\mathit{\theta }$

 

 

بافتراض أنَّ$\mathit{s}\mathit{i}\mathit{n}\mathit{\theta }\mathbf{ }\mathbf{=}\mathit{\theta }\mathbf{=}\mathbf{ }\frac{\mathbf{x}}{\mathbf{L}}$ فإنه يمكن كتابة القوة المعيدة على الصورة الآتية:

 

 

$\mathit{F}\mathbf{=}\mathbf{-}\mathit{m}\mathit{g}\frac{\mathbf{x}}{\mathbf{L}}$

$\mathit{F}\mathbf{=}\mathbf{-}\left(\frac{mg}{L}\right)\mathit{x}$

$\mathit{F}\mathbf{=}\mathbf{-}\mathit{k}\mathit{x}\mathbf{;}\mathit{k}\mathbf{ }\mathbf{=}\left(\frac{mg}{L}\right)$

 

 

شرطيّ الحركة التوافقية البسيطة

1)تتناسب القوة المعيدة طرديًّا مع مقدار الإزاحة x

 

2)اتجاه القوة المعيدة باتجاه معاكس لاتجاه الإزاحة x (باتجاه موقع الاتزان دائمًا)وذلك في حالة الزوايا الصغيرة.

 

 

 

 

وتحقق معادلة البندول البسيط شرطيّ الحركة التوافقية البسيطة.

 

 

 

الزمن الدوري للبندول البسيط

التردد الزاوي في نظام (كتلة-نابض)يُعبر عنه بالعلاقة

$\mathit{\omega }\mathbf{=}\mathbf{2}\mathit{\pi }\mathit{f}\mathbf{=}\sqrt{\frac{\mathbf{k}}{\mathbf{m}}}$

بتعويض قيمة k للبندول في معادلة التردد الزاوي للنابض نحصل على التردد الزاوي للبندول

$\mathit{\omega }\mathbf{=}\sqrt{\frac{\left({\displaystyle \frac{mg}{L}}\right)}{\mathbf{m}}}\mathbf{=}\sqrt{\frac{\mathbf{g}}{\mathbf{L}}}$

 باستخدام $\omega =\frac{2\mathrm{\pi }}{T}$ نحصل على الزمن الدوري للبندول

$\mathit{T}\mathbf{=}\mathbf{2}\mathbf{\pi }\sqrt{\frac{\mathbf{L}}{\mathbf{g}}}$

التشابه بين حركة نظام(كتلة-نابض) وحركة البندول البسيط

 

 

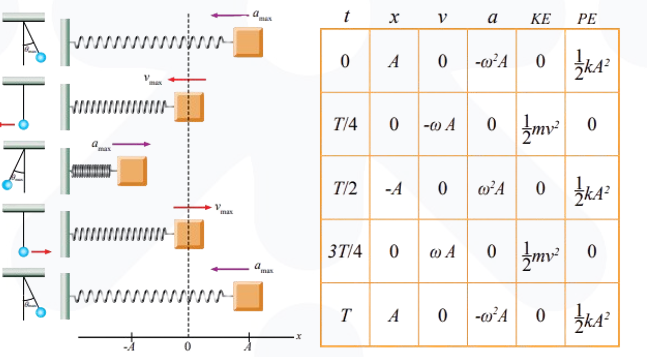
-الزمن الدوري للبندول يتغير بتغير طول البندول ولا يعتمد على كتلة البندول.

-عندما تزداد زاوية حركة البندول عن $\mathbf{10}\mathbf{°}$ تصبح الحركة التذبذبية لا تحقق شروط الحركة التوافقية البسيطة ومن ثم لا تنطبق عليها العلاقات الخاصة بهذه الحركة .

 

 

-من التطبيقات على البندول البسيط الساعة البندولية .

 

 

-عند سطح البحر يكون تسارع الجاذبية الأرضية$\mathbf{(}\mathbf{ }\mathbf{9}\mathbf{.}\mathbf{8}\mathit{m}\mathbf{/}\mathbf{ }{\mathit{s}}^{\mathbf{2}}\mathbf{ }\mathbf{)}$   فيكون الزمن الدوري للبندول ثانية واحدة عندما يكون طول الحبل$\mathbf{(}\mathbf{ }\mathbf{24}\mathbf{.}\mathbf{87}\mathit{c}\mathit{m}\mathbf{ }\mathbf{)}$ حسب معادلة الزمن الدوري:

$\mathit{T}\mathbf{=}\mathbf{2}\mathbf{\pi }\sqrt{\frac{\mathbf{L}}{\mathbf{g}}}$

أي أنَّ البندول يكمل ذبذبة واحدة في زمن مقداره ثانية واحدة.

 

تطبيقات حياتية على الحركة التوافقية البسيطة

1)الآلات الموسيقية

عند إزاحة وتر الغيتار عن موقع الاتزان مسافة معينة ثم تركه فإنه يتذبذب حول موقع الاتزان ذهابًا وإيابًا في حركة توافقية بسيطة وينتج من طاقة تذبذب الوتر صوت موسيقى يتلاشى تدريجيًّا نتيجة التناقص في طاقة الذبذبات.

 

2)القفز بالحبال المطّاطية(بنجي)                                                

نشاط رياضي ينطوي على القفز من مناطق شاهقة الارتفاع في حين يكون القافز مربوطًا بحبل مطاطي يحقق مواصفات الأمان فعندما يقفز الشخص ويصل الى أقصى إزاحة يبدأ بالتذبذب إلى أعلى وأسفل وتكون الحركة توافقية بسيطة إذا حققت شروطها.

 

 

 

3)البندول الإيقاعي(الرقاص)

 

 

جهاز يعمل على إصدار صوت منتظم ومكرر على شكل تكّة أو نقرة بعد إكمال ذبذبة كاملة ،أي خلال الزمن الدوري للبندول الذي يمكن تغييره عن طريق تغيير طول البندول باستخدام الكتلة القابلة للحركة على ذراع البندول لزيادة طوله أو إنقاصه.

 

-يوجد للبندول الإيقاعي عدة أنواع،ميكانيكي أو كهربائي أو إلكتروني.

-يستخدم الموسيقيون البندول الإيقاعي للتأكد من أن العزف يجري بوتيرة تامّة وأداء دقيق.

-يستخدم البندول الإيقاعي في الساعات للحفاظ على دقّة مماثلة لساعات اليد .

 

 

الحركة التوافقية المخمدة

 

 

هي الحركة التذبذبية التي تقل سعتها مع الزمن بسبب قوى المقاومة مثل قوة الاحتكاك.

-في الحركة التوافقية البسيطة درسنا النظام بافتراض عدم وجود قوى احتكاك وبالتالي كان النظام لا يفقد طاقة وسعة الذبذبة تبقى ثابتة ويستمر في الحركة الى اللانهاية .

-نفترض عدم وجود قوى احتكاك لتسهيل التعامل مع النظام .

 

 

-في الواقع يوجد قوى تؤثر بالنظام تعمل على تبديد طاقة النظام حيث تقل سعة التذبذب حتى تؤول الى الصفر فتتحول الطاقة الميكانيكية الى طاقة داخلية في الجسم والوسط الذي تتذبذب فيه.

-في حالة التخامد فإن الحركة التذبذبية لا تعد حركة توافقية بسيطة.

 

مثال:

استخدم جيولوجي بندولاً طوله $\mathbf{15}\mathbf{.}\mathbf{3}\mathit{c}\mathit{m}$ لقياس مقدار تسارع السقوط الحر في منطقة ما على سطح الأرض،فإذا أكمل البندول $\mathbf{52}$ دورة في مدة زمنية مقدارها $\mathbf{60}\mathit{s}$.أحسب تسارع السقوط الحر في تلك المنطقة.

 

الحل:

نحسب الزمن الدوري أوّلاً وهو حاصل قسمة الزمن الكلّي للدورات على الدورات الكاملة

 

 

                                                                 $\mathit{T}\mathbf{=}\frac{\mathbf{60}}{\mathbf{52}}\mathbf{=}\mathbf{1}\mathbf{.}\mathbf{15}\mathbf{ }\mathit{s}$ 

                                                                         $\mathit{T}\mathbf{=}\mathbf{2}\mathit{\pi }\sqrt{\frac{\mathbf{L}}{\mathbf{g}}}$

 

                                                                          ${\mathit{T}}^{\mathbf{2}}\mathbf{=}\mathbf{4}{\mathit{\pi }}^{\mathbf{2}}\frac{\mathbf{L}}{\mathbf{g}}$

 

 

                                                                       $\mathit{g}\mathbf{=}\mathbf{4}{\mathit{\pi }}^{\mathbf{2}}\frac{\mathbf{L}}{{\mathbf{T}}^{\mathbf{2}}}$

 

                                                                           $\mathit{g}\mathbf{=}\mathbf{4}\mathbf{(}\mathbf{3}\mathbf{.}\mathbf{14}{\mathbf{)}}^{\mathbf{2}}\mathbf{ }\frac{\mathbf{0}\mathbf{.}\mathbf{153}}{{\left(1.15\right)}^{\mathbf{2}}}$

 

 

                                                                              $\mathit{g}\mathbf{=}\mathbf{4}\mathbf{.}\mathbf{6}\mathit{m}\mathbf{/}{\mathit{s}}^{\mathbf{2}}$

 

 

 

مثال:

 

 

علقت فدوى كرة بنابض رأسي، وبعد استقرارها عند موقع الاتزان سحبتها إلى أسفل مسافة معينة كما في الشكل التالي، ثم تركتها تتذبذب حول ذلك الموقع  في حركة توافقية بسيطة بحيث تكمل  خمس دورات  في ثانيتين ،  حيث ثابت النابض$\mathbf{ }\mathbf{(}\mathit{k}\mathbf{=}\mathbf{350}\mathit{N}\mathbf{/}\mathit{m}\mathbf{)}$ حسب:

1)التردد

2)كتلة الكرة

 

3) كلاً من تسارع الكرة والقوة المعيدة  وقوة شد النابض عند موقع الاتزان

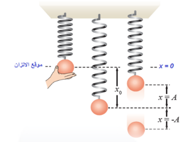
الحل:

)الزمن الدوري

                                                        $\mathit{T}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\frac{\mathbf{2}}{\mathbf{5}}\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{4}\mathbf{ }\mathit{s}$

التردد

$\mathit{f}\mathbf{=}\mathbf{ }\mathbf{ }\frac{\mathbf{1}}{\mathbf{T}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{0}\mathbf{.}\mathbf{4}}\mathbf{=}\mathbf{2}\mathbf{.}\mathbf{5}$

 

2)كتلة الكرة

                                                               $\mathit{T}\mathbf{ }\mathbf{=}\mathbf{2}\mathit{\pi }\sqrt{\frac{\mathbf{m}}{\mathbf{k}}}$

 

                                              $\mathit{m}\mathbf{=}\frac{{\mathbf{T}}^{\mathbf{2}}\mathbf{k}}{\mathbf{4}{\mathbf{\pi }}^{\mathbf{2}}}\mathbf{=}\frac{{\left(0.4\right)}^{\mathbf{2}}\mathbf{\times }\mathbf{350}}{\mathbf{4}{\left(3.14\right)}^{\mathbf{2}}}\mathbf{=}\mathbf{1}\mathbf{.}\mathbf{4}\mathit{k}\mathit{g}$

 

3) كلاً من تسارع الكرة والقوة المعيدة  وقوة شد النابض عند موقع الاتزان عند موقع الاتزان$\mathit{x}\mathbf{=}\mathbf{0}$

 

التسارع

                                                    $\mathit{a}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{-}\mathbf{ }\frac{\mathbf{k}}{\mathbf{m}}\mathbf{ }\mathit{x}\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{0}$

القوة

                                                                       $\mathit{F}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{-}\mathbf{ }\mathit{k}\mathit{x}\mathbf{ }\mathbf{=}\mathbf{0}$

 

قوة الشد

              $\mathit{F}\mathbf{=}{\mathit{F}}_{\mathbf{T}}\mathbf{-}\mathit{m}\mathit{g}\mathbf{\Rightarrow }\mathbf{0}\mathbf{=}{\mathit{F}}_{\mathbf{T}}\mathbf{-}\mathit{m}\mathit{g}\mathbf{\Rightarrow }{\mathit{F}}_{\mathbf{T}}\mathbf{=}\mathit{m}\mathit{g}\mathbf{=}\mathbf{1}\mathbf{.}\mathbf{4}\mathbf{\times }\mathbf{10}\mathbf{=}\mathbf{14}\mathit{N}$

 

الحل: