الفيزياء 11 فصل ثاني

 الحركة الدورية:

تتحرّك الأجسام بأشكال مختلفة، وأحد أشكالها يُسمّى الحركة الدورية:وهي حركة تكرّر نفسها على المسار نفسه في فترات زمنية متساوية.

 

من الأمثلة عليها:

1. دوران العجلة حول محورها.

 

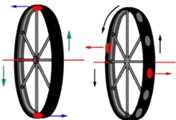
2. ودوران الكواكب حول الشمس.

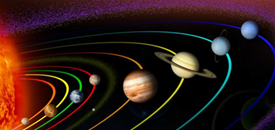
3. ويوجد نوع خاص من الحركة الدورية يُسمّى الحركة التذبذبية الاهتزازية وهي حركة دورية تُكرّر نفسها ذهابًا وإيابًا على المسار نفسه في فترات زمنية متساوية حول موقع الاتّزان، مثل:

• حركة الأرجوحة المُبيَّنة في الشكل.
• واهتزاز وتر آلة موسيقية.
• وتذبذب جُسيمات المادة الصلبة وغيرها.

والحركة التذبذبية حركة دورية، ولكن ليس كلّ حركة دورية هي حركة تذبذبية؛ فمثلاً: حركة الكواكب حول الشمس حركة دورية ولكنّها ليست تذبذبية كما في الشكل المرفق بالأعلى.

في هذا الدرس سنتعرّف نوعًا خاصًّا من الحركة التذبذبية يُسمّى الحركة التوافقية البسيطة.

 

أتحقّق:

ما الفرق بين الحركة التذبذبية والحركة الدورية؟

الحل:

الحركة الدورية تكرر نفسها على المسار نفسه في فترارت زمنية متساوية، مثل: دوران الأرض حول الشمس.

الحركة التذبذبية هي حركة دورية تكرر نفسها على المسار نفسه حول موقع اتزان، مثل حركة الأرجوحة. كل حركة تذبذبية هي دورية، لكن ليس كل حركة دورية تكون تذبذبية .

 

تُعدّ الحركة التوافقية البسيطة نمطًا خاصًّا من أشكال الحركة التذبذبية، ويشكّل فهمها الأساس لدراسة أنماط أكثر تعقيدًا من الحركات التذبذبية ودراسة الحركة الموجية أيضًا.

 

ويُعدّ النظام المُوضَّح في الشكل مثالً نموذجيًّا للحركة التوافقية البسيطة. يتكوّن النظام من نابض مُهمَل الكتلة مُثبَّت من أحد طرفيه، في حين يتصل الطرف الآخر بجسم كتلته  يتحرّك على سطح أفقي أملس.

 

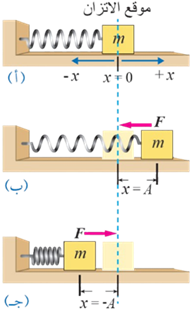
شرح الصور :

عندما لا يكون النابض مشدودًا أو مضغوطًا، يكون الجسم ساكنا عند الموقع (0=x)، ويُسمّى موقع الاتزان كما يبيّن الشكل (أ).

 

وعند إزاحة الجسم سواء إلى اليمين أو إلى اليسار مسافة (A) ثم تركه، فإن النظام يبدأ بالتذبذب ذهابًا وإيابًا حول موقع اتزانه، بحيث يمثّل موقع الجسم (x= A) سعة الذبذبة وهي أقصى إزاحة يتحرّكها الجسم عن موقع الاتزان، ويكون للسعة المقدار نفسه على يسار موقع الاتزان؛ (x= -A).

 

من خلال المعادلة التي تُعرف بقانون هوك: $F=-kx$

تدل الإشارة السالبة في قانون هوك على أن اتجاه القوّة المعيدة يكون دائمًا باتجاه موقع الاتزان؛ أي عكس اتجاه الإزاحة.

 

هذا يعني أنه عند إزاحة الجسم إلى يمين الموقع  (x=0)يكون اتجاه القوّة المعيدة نحو اليسار، كما يبيّن الشكل (ب).

عند إزاحته إلى يسار الموقع  (x=0)يكون اتجاه القوّة المعيدة نحو اليمين، كما يبيّن الشكل(ج). عند الموقع  فإن القوّة المؤثّرة في الجسم تساوي صفرًا.

بتطبيق القانون الثاني لنيوتن ($\Sigma F=ma$)توصّل إلى علاقة لحساب تسارع النظام، وهي:

$-kx=ma$

$a=-\frac{k}{m} x$

من خلال المعادلة يكون اتجاه التسارع باتجاه القوّة المعيدة.

وتُسمّى حركة النظام التي تحقّق هذا الشرط الحركة التوافقية البسيطة وهي حركة الجسم بتسارع يتناسب مقداره طرديًّا مع إزاحة الجسم عن موقع الاتزان، واتجاهه باتجاه موقع الاتزان ومعاكسًا لاتجاه الإزاحة. وبغياب قوى الاحتكاك يُفترَض أن تستمر هذه الحركة مدة لا نهائية؛ لأن قوّة النابض قوّة محافظة، لكن الأنظمة الحقيقية تتأثر بقوى الاحتكاك؛ لذا تتلاشى حركة الجسم تدريجيًّا إلى أن يتوقف.

---

أتحقّق: في الحركة التوافقية البسيطة، ما الكمّيتان من الكميات الآتية )الإزاحة، القوّة المُعيدة، التسارع( اللتان يكون اتجاههما دائمًا بالاتجاه نفسه؟ 

الحل:

الكميتان اللتان يكون لهما الاتجاه نفسه دائما: هما (القوة المعيدة، التسارع)، في حين يكون اتجاه الإزاحة معاكسة لاتجاههما.

 

 

مثال: جسم كتلته (m) متصل بنابض ويتحرك حركة توافقية بسيطة على سطح أفقي أملس، كما يبيّن الشكل النقطة تمثّل موقع الاتزان، والنقطتان)و (A-) تمثّلان أقصى موقعين للجسم عن موقع الاتزان).

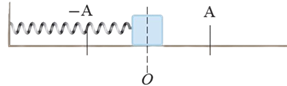
أ. أحدّد المواقع التي يكون للقوةّ المعيدة والتسارع فيها قيمة عظمى، مع توضيح اتجاه القوة والتسارع في كل موقع منها. وأحدّد المواقع التي تكون فيها القوّة المعيدة والتسارع تساوي صفرًا.

ب. أحدّد المواقع التي يكون للسرعة فيها قيمة عظمى، والمواقع التي تكون السرعة فيها تساوي صفرًا.

الحل:

أ. القوّة المعيدة تتناسب طرديًّا مع التسارع، ولهما الاتجاه نفسه. وباستخدام العلاقة.

$a=-\frac{k}{m} x$ فإن التسارع يتناسب طرديًّا مع الإزاحة ومعاكسًا لها في الاتجاه.

فيكون للتسارع (والقوة المعيدة) قيمة عظمى عند الموقع $A$، باتجاه $-X$

ولكل منهما قيمة عظمى عند الموقع ($-A$) وباتجاه ($+X$) وتكون قيمة كل منهما صفرًا في الموقع.

 

ب. عند وصول الجسم إلى أقصى إزاحة تكون سرعته صفرًا، أي أن سرعته تساوي صفرًا في الموقعين (A)  و (A-) 

أما لحظة مرور الجسم في الموقع  (0)فيكون لسرعته قيمة عظمى.

يمكن تلخيص الإجابة في الجدول الآتي:-

---

مثال (2):

ضُغِط جسم متّصل بنابض موضوع على سطح أفقي أملس إلى نقطة تبعد مسافة 5 cm عن موقع اتّزانه على نحو ما هو مبيَن في الشكل ، وتُرِك يتذبذب ذهابًا وإيابًا. إذا كان مقدار القوّة المُعيدة عند تلك النقطة  فأحسب ما يأتي:

أ . مقدار سَعة الذبذبة.

ب. ثابت مرونة النابض.

ج. القوّة المُعيدة عندما يُصبح الجسم على بعد  عن موقع الاتّزان في أثناء عودته.

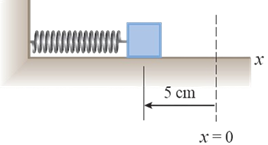
الحل:

أ . سَعة الذبذبة هي أقصى إزاحة عن موقع الاتّزان، وتساوي $A=0.05m$

ب. ثابت مرونة النابض K 

ج. القوّة المُعيدة عند الموقع: x=-2

$F2cm=-k x=-80\times (-0.02)=1.6 N$

الإشارة الموجبة للقوّة تدل على أن القوّة باتجاه محور x الموجب؛ أي بعكس اتجاه الإزاحة

---

التمثيل الرياضي للحركة التوافقية البسيطة:

الحركة التوافقية البسيطة هي حركة دورية تتكرّر بانتظام، وهذا النوع من الحركة يُوصف باستخدام مفاهيم خاصة، مثل: الزمن الدوري، والتردد.

لتوضيح المفاهيم الخاصة بالحركة التوافقية، سوف ندرس حركة نظام يتكوّن من جسم يتصل بنابض معلّق رأسيًّا، كما يبيّن الشكل.

 

شرح: عند سحب الجسم إلى الأسفل وتركه يهتز، بالتزامن مع سحب شريط الورق أفقيًّا بسرعة ثابتة، سوف يرسم القلم المثبَّت في طرف النابض على شريط الورق منحنى يبيّن التغير في الإزاحة مع الزمن للحركة التوافقية البسيطة.

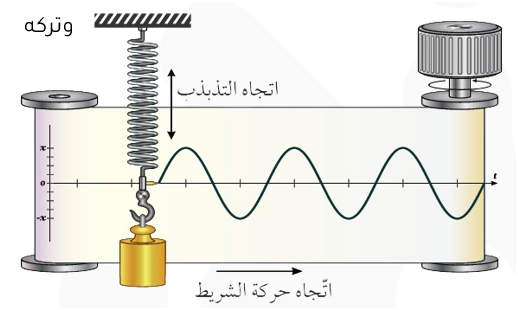
تُعرَّف الدورة )الذبذبة الكاملة( بأنها الحركة التي يُحدثها الجسم المهتزّ كي يمرّ بالنقطة الواحدة في مسار حركته بالاتجاه نفسه مرّتين متتاليتين.

أمّا الزمن الدوري (T) فهو الزمن اللازم لإتمام دورة كاملة، ويعتمد الزمن الدوري على كل من ثابت المرونة للنابض (K)وكتلة الجسم (m) حسب العلاقة الآتية:

$T = 2\pi \sqrt[]{\frac{m}{k}}$

في حين يُعرَّف التردد (f) بأنه عدد الدورات في الثانية الواحدة، ويُقاس في النظام الدولي للوحدات بوحدة (s-1) وتُعرَف بالهيرتز (Hz) ويتناسب التردد عكسيًّا مع الزمن الدوري حسب العلاقة الآتية:

$f=\frac{1}{T}$

 

كما توصف الحركة التوافقية باستخدام التردد الزاوي ω وهو عدد الدورات الكاملة في وحدة الزمن مضروبًا في

 

2π وهو مقياس لمدى سرعة حدوث الذبذبات؛ فكلما زاد عدد الذبذبات في وحدة الزمن زاد مقدار  

 

ωويُقاس التردد الزاوي بوحدة

 

Hz ، ويحسب بالعلاقة:

$\omega =\frac{2\pi }{T}=2\pi f$

يبيّن الشكل منحنى )الإزاحة – الزمن( للحركة التوافقية، بدءًا من اللحظة (t=0) ، حيث بدأت حركة النظام من أقصى إزاحة  $(x=+A)$ كما يتضح من الشكل أن منحنى تغير الإزاحة $x$ مع الزمن t للحركة التوافقية البسيطة يُمثّل بيانيًّا باقتران جيب التمام، ويُعبَّر عنه بالعلاقة:

$x\left(t\right)=A\cos \omega t$

 

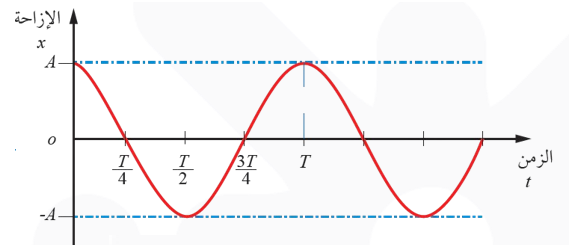
نطبق هذه الصيغة على الحركة التوافقية البسيطة التي تبدأ من الموقع (A) عند الزمن ( t = 0 )؛ لذلك لا تُعدّ هذه العلاقة صيغة عامة للحركة التوافقية البسيطة، بل حالة خاصة.

 

 

أما إذا بدأ الجسم من إزاحة مقدارها

 

xi  عند اللحظة 

 

t = 0 ؛ كما يبيّن الشكل فإنّ الصيغة العامة لمعادلة الحركة التوافقية البسيطة تعطى بالعلاقة الآتية :

$x\left(t\right)=A\cos (\omega t+\varphi )$

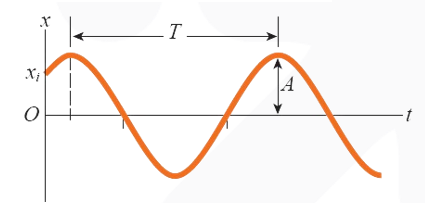
حيث ϕ  ثابت الطور (أو زاوية الطور الابتدائية(، وهي الزاوية التي تحدّد موقع الجسم عند لحظة بداية الحركة.

---

 

البندول البسيط:

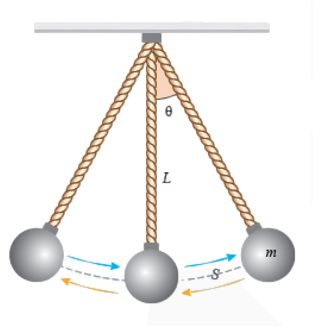
يتكوّن البندول البسيط من جسم )قد يكون كرة (كتلته (m) معلّق بواسطة خيط خفيف كتلته مهملة وطوله (L). عند تعليق البندول كما هو مبين في الشكل ثم سحبه إلى اليمين )أو اليسار( بحيث يصنع الخيط زاوية  $\theta$ مع موقع الاتزان ثم تركه، فإنه يتذبذب ذهابًا وإيابًا على المسار نفسه حول موقع الاتزان، بحيث تقطع الكرة مسافة (S) تشكّل قوسًا من دائرة نصف قطرها يساوي طول خيط البندول. تتأثر الكرة في أثناء حركتها بقوّة الشد في الخيط (T)، وقوّة الجاذبية الأرضية (mg).

يبيّن الشكل مخطط الجسم الحر للكرة عند أقصى إزاحة لها عن موقع الاتزان. باختيار محور  $x$  باتجاه يوازي المماس للقوس الدائري ورسم محور  $y$ عموديًّا عليه، فإنه يمكن تحليل قوّة الجاذبية إلى مركّبتين: مركّبة مماسي ($mg \sin \theta$) ومركّبة عمودية على المماس $mg \cos \theta$  

وبما أنه لا يوجد حركة على امتداد المحور  (Y) فإن القوّة المحصلة بهذا الاتجاه تساوي صفرًا:

$\Sigma Fy=T-mg \cos \theta =0$

أما القوّة المحصلة باتجاه المماس فهي تساوي:

$\Sigma Fx=mg \sin \theta$

 

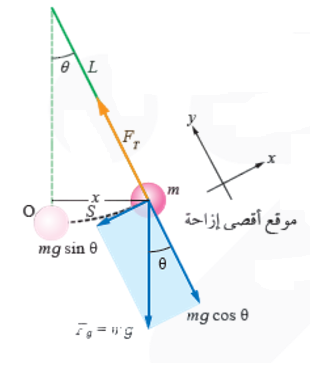
وهي قوّة يتغير اتجاهها بتغير الموقع، بحيث تتجه دائمًا نحو موقع الاتزان، وبعكس اتجاه الإزاحة، إذا فهي تمثّل قوّة معيدة تعطى بالعلاقة الآتية:

$F=-mg \sin \theta$

عندما تكون الزاوية $\theta$ صغيرة $(\theta °\le 10)$ فإنّ مقدار الزاوية $\theta$ بوحدة راديان يساوي تقريبًا ، وطول القوس S يساوي تقريبًا الإزاحة الأفقية ْx. في هذه الحالة يمكن وصف حركة البندول بأنها حركة توافقية بسيطة. ويمكن إعادة كتابة العلاقات السابقة كما يأتي:

$\sin \theta =\theta =\frac{x}{L}$

 

والقوّة المعيدة تساوي تقريبًا:

$F=-mg \theta =-mg \frac{x}{L}$

 

تحقّق هذه المعادلة شروط الحركة التوافقية البسيطة، إذ يتناسب مقدار القوّة المعيدة طرديًّا مع الإزاحة، واتجاهها بعكس اتجاه الإزاحة.

---

 

الزمن الدوري للبندول البسيط:

يمكن التعبير عن القوّة المعيدة للبندول البسيط بالصورة الآتية:

$F=-\frac{mg}{L} X$

 

وتتفق هذه المعادلة مع الصورة العامة للقوّة المعيدة في قانون هوك: $F=-kx$ ؛ لذا فإن حركة البندول البسيط في هذه الحالة هي حركة توافقية بسيطة تتشابه مع حركة نظام )الكتلة-النابض(. وعند مقارنة كلا الحركتين نتوصّل إلى الآتي:

◘ قيمة ثابت النابض K، في قانون هوك يقابله في حالة البندول المقدار ($\frac{mg}{L}$).

◘ الزمن الدوري للنابض يعطى بالعلاقة ($T=2\sqrt[]{\frac{m}{k}}$)، وفي حالة البندول البسيط فإنّ $k=\frac{mg}{L}$ وبذلك فإن الزمن الدوري للبندول البسيط يعطى بالعلاقة:              

$T=2\pi \sqrt[]{\frac{L}{g}}$

توضح هذه العلاقة أن الزمن الدوري للبندول البسيط، الذي يحقق شرط الحركة التوافقية البسيطة، يبقى ثابتًا ما دام طول الخيط وتسارع السقوط الحر ثابتًا.

---

 

القفز بالحبال المطّاطية (بنجي):

يُعدُّ القفز بالحبال أو ما يُعرف بالبنجي على نحو ما يظهر في الشكل تطبيقًا على الحركة التوافقية البسيطة، وهو نشاط رياضي ينطوي على القفز من مناطق شاهقة الارتفاع، في حين يكون القافز مربوطًا بحبل مطّاطي يُحقّق مواصفات الأمان؛ ويقفز من مناطق ثابتة كالجسور والمباني، أو متحرّكة كالقفز من منطاد أو من طائرة عمودية.

وأُدخلت في السنوات الأخيرة رياضة القفز من الرافعات إلى بعض المدن الترفيهية بوصفها وسيلة للترفيه. وعندما يقفز الشخص ويصل إلى أقصى إاحة يبدأ بالتذبذب إلى أعلى وأسفل، وتكون الحركة توافقية بسيطة إذا تحقّقت شروطها.

 

الحركة التوافقية المُخمدة:

عند دراسة الحركة التوافقية البسيطة (مثل حركة البندول وحركة الكتلة المعلقة بالنابض وغيرها) افترضنا عدم وجود قوى احتكاك؛ ولذلك فالنظام لا يفقد طاقة، وسعة التذبذب تبقى ثابتة ويستمر في الحركة إلى اللانهاية، وهذا الافتراض لتسهيل التعامل مع الحركة التوافقية البسيطة رياضيًّا، لكن في الواقع تقل سعة التذبذب مع الزمن بالتدريج حتى تتوقف الحركة التذبذبية؛ لأن قوى أخرى تؤثر في النظام (مثل قوى الاحتكاك) فتبدّد من طاقة النظام حتى تؤول سعة التذبذب إلى الصفر، حيث تتحول الطاقة الميكانيكية إلى طاقة داخلية في الجسم والوسط الذي يتذبذب فيه.

 

بوجهٍ عام فإن أنظمة التذبذب الطبيعية تكون متخامدة. ويطلق على الحركة التذبذبية التي تقل سعتها مع الزمن بسبب قوى المقاومة؛ مثل قوة الاحتكاك اسم الحركة التوافقية المخمدة.

في حالة التخامد فإن الحركة التذبذبية لا تُعدّ حركة توافقية بسيطة.

من الأمثلة على الحركة التوافقية المخمدة غالق الباب الهيدروليكي أو ما يُسمّى ردّاد الباب على نحو ما هو مبيَّن في الشكل حيث يوجد في داخل الغالق نابض ينضغط عند فتح الباب، وعند ترك الباب يعود النابض لطوله الأصلي فيؤثّر بقوّة في الزيت لدفعه عبر ثقب صغير؛ إذ تعمل هذه القوّة على تخميد النظام؛ لذا، يُغلق الباب ببطء.