الدرس الرابع: الحقائق المترابطة
الحقائق المترابطة
مثلث الحقائق
تمهيد 
تعلمنا في الدرس السابق العلاقة بين القسمة والضرب لإيجاد ناتج القسمة، حيث لِكُلِّ جُمْلَةِ قِسْمَةٍ جُمْلَةُ ضَرْبٍ مُرْتَبِطَةٌ بِها.
أستكشف
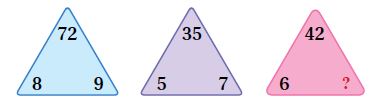
ما الْعَدَدُ الْمَفْقودُ في الْمُثَلَّثِ أَدْناهُ؟ 
ألاحظ أن هناك علاقة خفية بين الأعداد في كل مثلث، فمن خلال المثلث مثلا أجد أن
سوف نتعلم في هذا الدرس استعمال العلاقة بين القسمة والضرب لإيجاد بعض حقائق الضرب والقسمة.
أتعلم
الْحَقائِقُ الْمُتَرابِطَةُ related fact هِيَ مَجْموعَةُ جُمَلِ الضَّرْبِ أَوِ الْقِسْمَةِ الَّتي تُسْتَعْمَلُ فيها الْأَعْدادُ نَفْسُها.
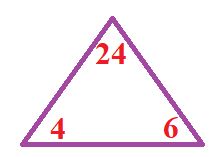
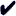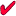يُساعِدُني مُثَلَّثُ الْحَقائِقِ facts triangle عَلى إيجادِ حَقائِقِ الضَّرْبِ وَالْقِسْمَةِ الْمُتَرابِطَةِ لِثَلاثَةِ أَعْدادٍ، إِذْ يُمَثِّلُ الْعَدَدُ في أَعْلى الْمُثَلَّثِ ناتِجَ ضَرْبِ الْعَدَدَيْنِ في الْأَسْفَلِ، وَعِنْدَ قِسْمَةِ الْعَدَدِ في أَعْلى الْمُثَلَّثِ عَلى أَحَدِ الْعَدَدَيْنِ في الْأَسْفَلِ، فَإِنَّ الْإِجابَةَ تَكونُ الْعَدَدَ الْآخَرَ الَّذي في الْأَسْفَلِ.
يُمْكِنُني اسْتِعْمالُ الْأَعْدادِ في جُمْلَةِ ضَرْبٍ أَوْ قِسْمَةٍ لِكِتابَةِ جُمَلِ الضَّرْبِ وَالْقِسْمَةِ الْأُخْرى الْمُرْتَبِطَةِ بِها.
ألاحظ أنه من نفس المثلث أستطيع إيجاد حقائق الضرب والقسمة.
أَتَحَدَّثُ: كَيْفَ يُساعِدُني مُثَلَّثُ الْحَقائِقِ عَلى كِتابَةِ الْحَقائِقِ الْمُتَرابِطَةِ لِثَلاثَةِ أَعْدادٍ؟
من خلال النظر إلى مثلث الحقائق أجد أن العدد الذي في أعلى المثلث يمثل ناتج ضرب العددين في الأسفل، أما عند قسمة العدد في أعلى المثلث على أحد العددين في الأسفل، فإن الإجابة تكون العدد الآخر في الذي في الزاوية الأخرى في الأسفل.
مثال إضافي للتوضيح: أَسْتَعْمِلُ مُثَلَّثَ الْحَقائِقِ لِكِتابَةِ الْحَقائِقِ الْمُتَرابِطَةِ:
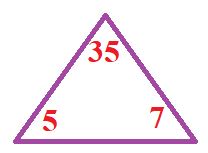
ألاحظ أن في المثلث ثلاثة أَعْدادٍ، إِذْ يُمَثِّلُ الْعَدَدُ في أَعْلى الْمُثَلَّثِ (35)ناتِجَ ضَرْبِ الْعَدَدَيْنِ في الْأَسْفَلِ (7 ، 5)، وَعِنْدَ قِسْمَةِ الْعَدَدِ في أَعْلى الْمُثَلَّثِ عَلى أَحَدِ الْعَدَدَيْنِ في الْأَسْفَلِ، فَإِنَّ الْإِجابَةَ تَكونُ الْعَدَدَ الْآخَرَ الَّذي في الْأَسْفَلِ. ويكون ذلك على النحو الآتي:
مثال إضافي للتوضيح: أَسْتَعْمِلُ مُثَلَّثَ الْحَقائِقِ لِكِتابَةِ الْحَقائِقِ الْمُتَرابِطَةِ: 