تعرف الخوارزميات بأنها مجموعة من الخطوات المنظمة لحل مشكلة ما .
تستخدم الخوارزميات في الكثير من الأمور الحياتية والعلمية ، فمن الأمثلة عليها في الحياة ..
- • دليل تركيب وتشغيل جهاز كهربائي جديد .
- • خطوات الطبخ لإعداد طعام معين .
وتستخدم كذلك الأمر في الرياضيات عندما نصف مثلاً خطوات أو كيفية اشتقاق الجذور غير التربيعية وغيرها
- يوجد ( 3 ) طرق لكتابة الخوارزميات :
- الخوارزميات المكتوبة بالكلمات .
- الخوارزميات المكتوبة بطريقة شبه رمزية .
- الخوارزميات الممثلة بمخططات سير العمليات .
تنبيه شديد الأهمية ...
أياً كانت الطريقة المستخدمة للتعبير عن الخوارزمية فإنه لا يمكن تطبيقها إلا عن طريق تتبع خطواتها بالترتيب .
أولاً : الخوارزميات المكتوبة بالكلمات ..
- وفيها تكتب الخوارزمية عن طريق جمل ( خطوات ) متسلسلة دون استخدام الرموز فيها .
مثال 1 : الخوارزمية الآتية تستخدم لتحديد إذا كان العدد يقبل القسمة على ( 11 ) أم لا .
- اجمع الأرقام في المواضع الفردية من العدد .
- اجمع الأرقام في المواضع الزوجية من العدد .
- جد الفرق المطلق بين المجموعين في الخطوتين السابقتين .
- إذا كان الفرق المطلق ( 0 ) أو يقبل القسمة على ( 11 ) فإن العدد يقبل القسمة على ( 11 ) وإلا فإنه لا يقبل القسمة على ( 11 )
المطلوب : طبق الخوارزمية على الأعداد الآتية لبيان إذا كانت تقبل القسمة على ( 11 ) أم لا .
a)
86146
|
الرقم |
6 |
4 |
1 |
6 |
8 |
|
الموضع |
1 |
2 |
3 |
4 |
5 |
- مجموع الأرقام بالمواضع الفردية :
- مجموع الأرقام بالمواضع الزوجية:
- الفرق المطلق بينهم (الأكبر – الأصغر):
- العدد ( 86146 ) لا يقبل القسمة على ( 11 )
لأن الفرق المطلق بين المجموعين هو ( 5 ) وهو لا يقبل القسمة على ( 11 ) ولا يساوي صفرا .
b)
83655
|
الرقم |
5 |
5 |
6 |
3 |
8 |
|
الموضع |
1 |
2 |
3 |
4 |
5 |
- مجموع الأرقام بالمواضع الفردية:
- مجموع الأرقام بالمواضع الزوجية:
- الفرق المطلق بينهم (الأكبر – الأصغر):
- العــدد ( 83655 ) يقبل القسمــة على ( 11 ) لأن الفرق المطلق يساوي ( 11 ) وهو يقبل القسمة على ( 11 ) .
الخوارزميات المكتوبة بطريقة شبه رمزية
تُكتَب الخوارزمية أيضًا باستعمال الطريقة شبه الرمزية، وفيها توصَف الخوارزمية بخطوات مُتسلسِلة مُرقَّمة تتضمَّن العديد من الرموز. غير أنَّ تتبُّع الخوارزمية المكتوبة بهذه الطريقة يكون صعبًا في بعض الأحيان، ويحتاج إلى تنظيم؛ لذا يُمكِن استعمال جدول التتبُّع لتدوين القيمة الناتجة من كل خطوة أثناء تطبيق الخوارزمية.
مثال
أتأمَّل الخوارزمية الآتية المكتوبة بالطريقة شبه الرمزية، ثمَّ أُجيب عن كلٍّ ممّا يأتي:

1) أُطبِّق الخوارزمية باستعمال جدول التتبُّع لإيجاد مُخرَجاتها.
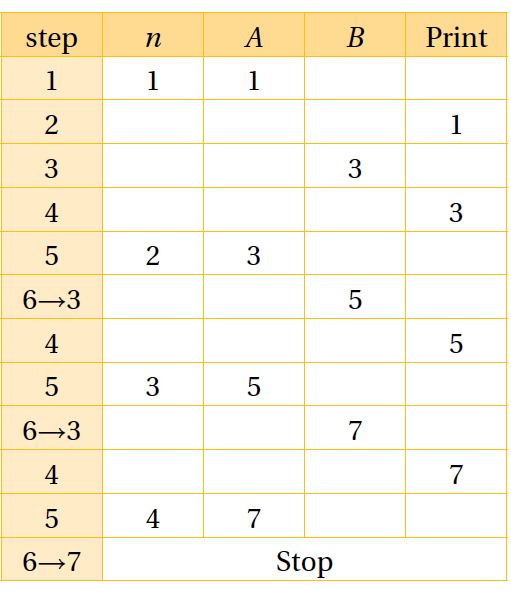
2) أَصِف مُخرَجات الخوارزمية.
تُمثِّل مُخرَجات الخوارزمية الأعداد الفردية الموجبة التي تقلُّ عن العدد
الخوارزميات المُمثَّلة بمُخطَّطات سَيْر العمليات
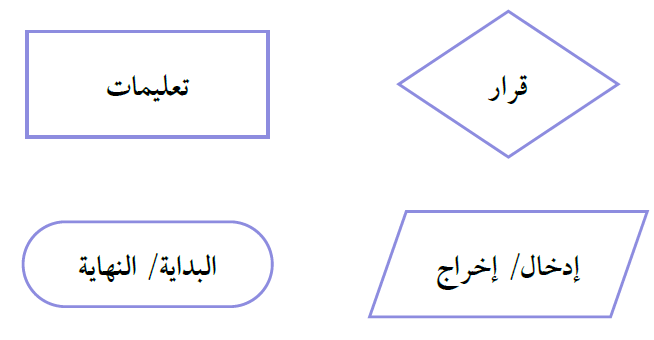
يُمكِن أيضًا تمثيل الخوارزمية باستعمال مُخطَّط سَيْر العمليات؛ وهو مُخطَّط يتكوَّن من أشكال هندسية مُرتبِطة بأسهم وخطوط تَصِف خطوات الخوارزمية وسَيْر العمليات فيها. بوجه عام، تُستعمَل الأشكال )الصناديق( الآتية للدلالة على خطوات مُحدَّدة في الخوارزمية:
مثال:
أتأمَّل الخوارزمية الآتية المُمثَّلة بمُخطَّط سَيْر العمليات، ثمَّ أُجيب عن كلٍّ ممّا يأتي:
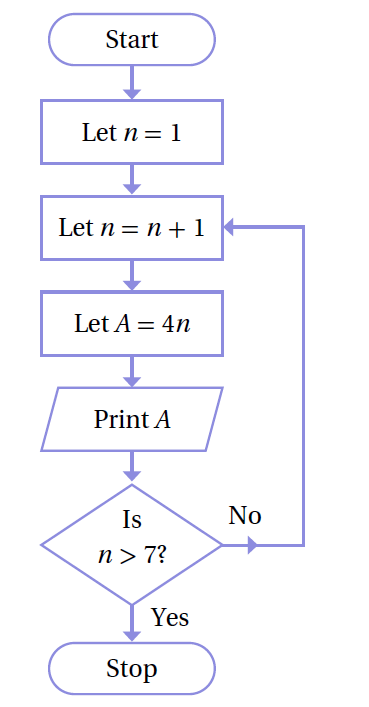
1) أُطبِّق الخوارزمية باستعمال جدول التتبُّع لإيجاد مُخرَجاتها.
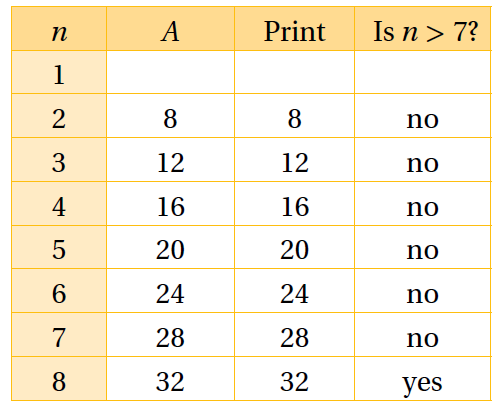
مُخرَجات الخوارزمية هي:
2) أَصِف مُخرَجات الخوارزمية.
تُمثِّل مُخرَجات الخوارزمية مضاعفات العدد 4، التي تزيد على أو تساوي 8، وتقلُّ عن 36
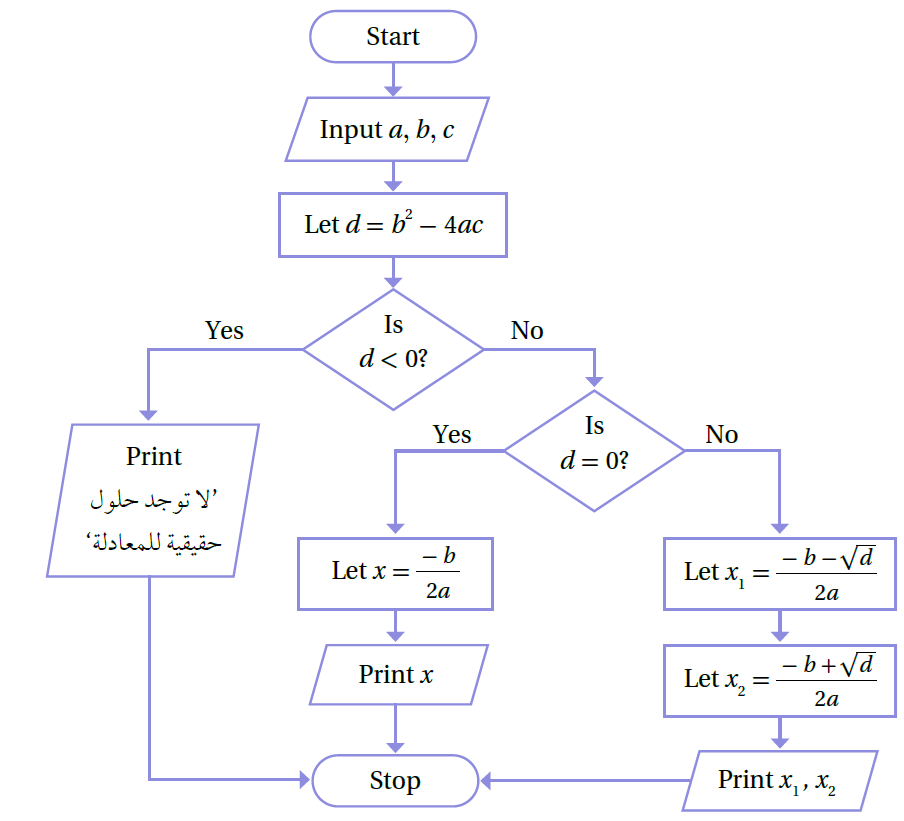
مثال:
تُستعمَل الخوارزمية الآتية لإيجاد الجذور الحقيقية للمعادلة التربيعية: أُطبِّق الخوارزمية، ثمَّ أُحدِّد المُخرَج لكلٍّ من المعادلات التربيعية التالية: