رياضيات فصل أول

 

يمكن ان تتقاطع الدائرتان المرسومتان في مستوى واحد في نقطة واحدة، او نقطتين، 

وقد لا تتقاطعان ابدا. وتسمى الدائرتان المتقاطعتان في نقطة واحدة فقط دائرتين متماستين .
مفهوم اساسي: 

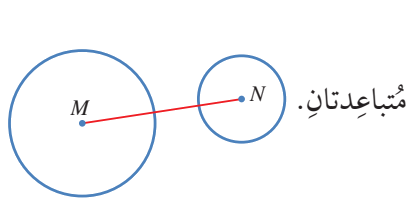
اذا رسمت دائرتان في مستوى واحد، فان وضعهما بالنسبة الى بعضهما ينحصر في الحالات الاتية: 

1) متباعدتان.

2) متقاطعتان في نقطتين.

3) احدهما داخل الاخرى.

4) مشتركتان في نقطة واحدة، اي انهما متماستان. ولهذا الوضع صورتان: 

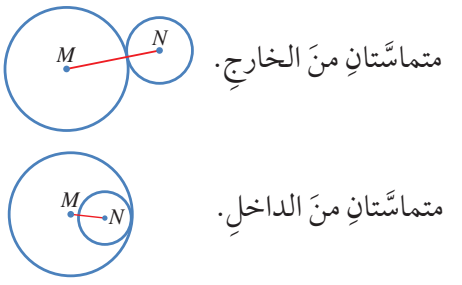
اذا كان المستقيم مماسا لكل من دائرتين، فانه يسمى مماسا مشتركا 

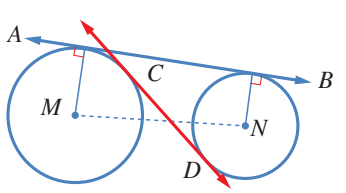
واذا قطع المماس المشترك القطعة المستقيمة الواصلة بين مركزي الدائرتين، 

فانه يسمى المماس المشترك الداخلي، والا فانه يسمى المماس المشترك الخارجي. 

ففي الشكل المجاور، $\overleftrightarrow{AB}$ مماس مشترك خارجي، و $\overleftrightarrow{CD}$ مماس مشترك داخلي .

يمكن رسم مماس واحد فقط للدائرة عند نقطة عليها، ويمكن ايضا رسم مماسين 

للدائرة من نقطة خارجها، فما عدد المماسات المشتركة التي يمكن رسمها للدائرتين؟ 

تعتمد اجابة هذا السؤال على وضع الدائرتين بالنسبة الى بعضهما 

مثال:

كم مماسا مشتركا يمكن رسمه للدائرتين في الشكل الاتي؟

ارسم المماسات، ثم اصنفها الى خارجية وداخلية .

الحل: 

ارسم القطعة المستقيمة الواصلة بين مركزي الدائرتين، 

ثم ارسم المماسات التي تقطعها بلون احمر، 

والمماسات التي لا تقطعها بلون ازرق.

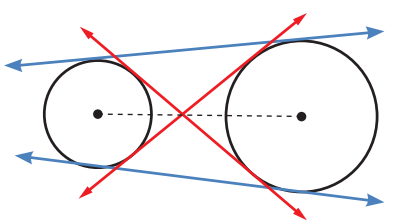
الاحظ انه يوجد للدائرتين مماسان داخليان، واخران خارجيان 

طول المماس المشترك

يمكن حساب طول المماس المشترك (المسافة بين نقطتي التماس على الدائرتين).

بطريقة مماثلة لحساب طول المماس المرسوم من نقطة خارج الدائرة الى نقطة عليها 

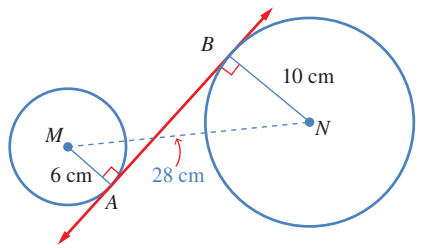
مثال 

اجد طول $\overline{AB}$ في الشكل المجاور .

الحل: 

أمد $\overline{MA}$ على استقاته، ثم ارسم من N عمودا على امتداد $\overline{MA}$،

ثم نقطة تقاطع العمود معها C . 

$m\angle NBA=m\angle BAC=90°$

                    $m\angle ACN=90°$

                    $m\angle BNC=90°$

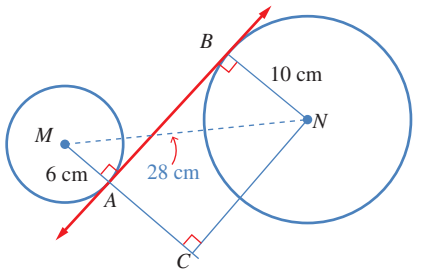
اذن، الشكل الرباعي ACNB  مستطيل؛ لان زواياه الاربع قوائم أي أن: 

$AB=NC$

ولان، اطبق نظرية قيثاغورس على المثلث قائم الزاوية MCN لاجد CN: 

  ${\left(CN\right)}^2={\left(MN\right)}^2-{\left(MC\right)}^2$

$={\left(28\right)}^2-{\left(6+10\right)}^2$

${\left(CN\right)}^2=784-256=528$

$CN=\sqrt{528}\approx 23$

$AB=CN\approx 23cm$

مثال: من الحياة

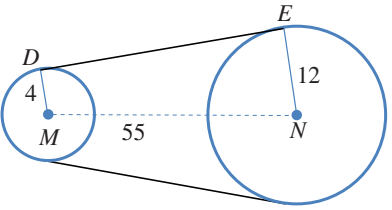
دراجات: تلتف في دراجة هوائية سلسلة معدنية على عجلتين مسننتين دائرتين، 

نصف قطر الصغرى $4cm$، ونصف قطر الكبرى $12cm$، والمسافة بين مركزيهما $55cm$.

اجد طول السلسلة بين نقطتي  تماسها مع المسننتين.

الحل: 

المطلوب هو حساب طول $\overline{DE}$. ارسم من M عمودا على $\overline{NE}$، 

ثم اسمي نقطة تقاطعه معها F كما في الشكل المجاور :

$m\angle NED=m\angle MDE=90°$

$m\angle MFE=90°$

$m\angle DMF=90°$

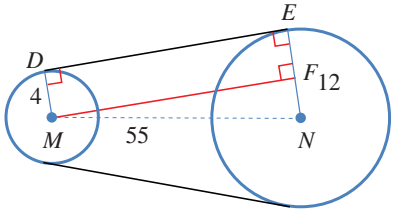
اذن، الشكل الرباعي MDEF مستطيل، لان زواياه الاربع قوائم 

ولان، اطبق نظرية فيثاغورس على المثلث قائم الزاوية MFN لاجد طول $\overline{MF}$:

  ${\left(MF\right)}^2={\left(MN\right)}^2-{\left(FN\right)}^2$

$={\left(55\right)}^2-{\left(12-4\right)}^2$

${\left(MF\right)}^2=3025-64=2961$

$MF=\sqrt{2961}=54.4$

$DE=MF=54.4cm$