رياضيات7 فصل أول

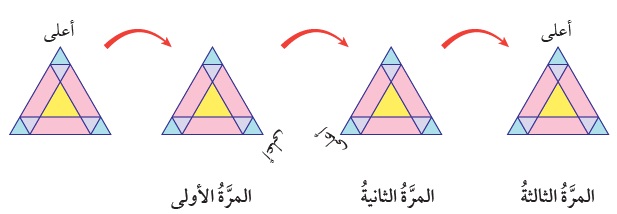
مفهوم أساسي : يعملُ الدورانُ  (Rotation) على تحريكِ كلِّ نقطةٍ في الشكلِ الأصليِّ بزاويةٍ محددةٍ واتجاهٍ محددٍ حولَ نقطةٍ ثابتةٍ تُسمّى مركزَ الدورانِ ، (Center of rotation) معَ المحافظةِ على أبعادِ الشكلِ الأصليِّ وزواياهُ.

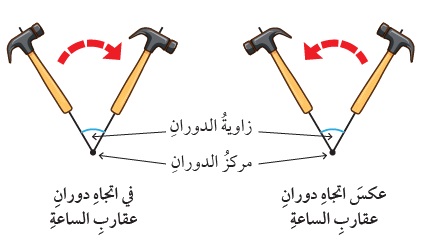
يمكنُ استعمالُ ورقةٍ شفّافةٍ لرسمِ صورةِ شكلٍ تحتَ تأثيرِ دورانٍ بزاويةٍ مُحدَّدةٍ حولَ مركزِ دورانٍ محدد.

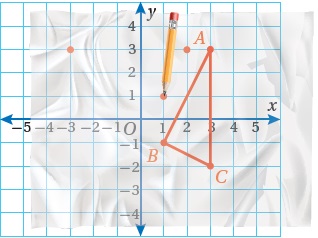
مثال1:أستعملُ ورقةً شفّافةً لرسمِ صورةِ $\mathbf{∆}\mathbf{ABC}$في الشكلِ المجاورِ الناتجةِ منْ دورانِ مركزِهِ نقطةُ الأصلِ بزاويةِ (°90) عكسَ عقاربِ الساعةِ، ثمَّ أكتبُ إحداثياتِ رؤوسِ الصورةِ$\mathbf{∆}\mathbf{A}\mathbf{\text{'}}\mathbf{B}\mathbf{\text{'}}\mathbf{C}\mathbf{\text{'}}$

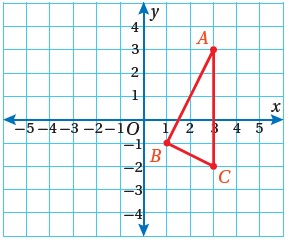
الخطوةُ 1: أرسمُ رؤوسَ المثلثِ على ورقةٍ شفّافةٍ.

أضعُ الورقةَ فوقَ المثلثِ بحيثُ تغطّي أيضًا مركزَ الدورانِ، ثمَّ أرسمُ بالقلمِ رؤوسَ المثلثِ وأضعُ إشارةً فوقَ محورِ x الموجب 

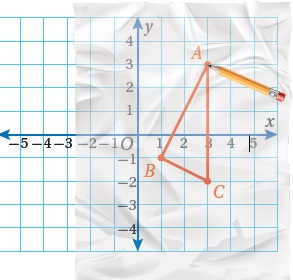
الخطوةُ 2: أُدوِّرُ الشكلَ، ثمَّ أُحدِّدُ رؤوسَ الصورةِ.

أضغطُ برأسِ القلمِ عندَ مركزِ الدورانِ(نقطةُ الأصلِ)، ثمَّ أُدوِّرُ الورقةَ بزاويةِ  (°90) عكسَ عقاربِ الساعةِ، بحيثُت نطبقُ الإشارةُ الّتي رسمتُها على محورِ y الموجب ثم أُحدِّدُ رؤوسِ الصورةِ.  

الخطوةُ 3: أرسمُ الصورةَ.

أرسمُ الصورةَ بالتوصيلِ بينَ إحداثياتِ رؤوسِها، ثمَّ أُسمّيها $∆\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}$

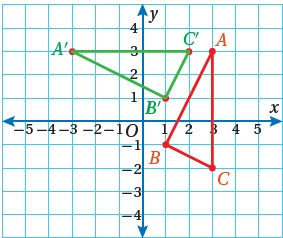
إحداثياتُ رؤوسِ الصورةِ $∆\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{C}\text{'}$ هي $\mathrm{A}\text{'}(-3, 3), \mathrm{B}\text{'}(1, 1), \mathrm{C} \text{'}(2, 3)$

 

مفهومٌ أساسيٌّ:

عندَ دورانِ النقطةِ (a,b) حولَ نقطةِ الأصلِ، فإنَّ إحداثيَّيْها يتغيرانِ بحسبِ القواعدِ الآتيةِ: 

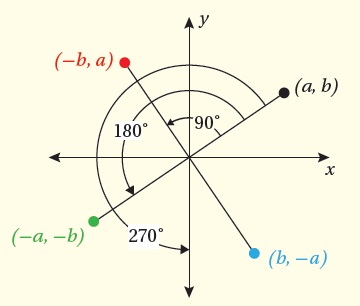
• الدورانُ بزاويةِ (°90) عكس عقاربِ الساعةِ أو (°270 مع عقاربِ الساعةِ):

$\mathbf{(}\mathbf{a}\mathbf{,}\mathbf{ }\mathbf{b}\mathbf{)}\mathbf{ }\mathbf{\to }\mathbf{ }\mathbf{(}\mathbf{-}\mathbf{b}\mathbf{,}\mathbf{ }\mathbf{a}\mathbf{)}$

• الدورانُ بزاويةِ (°180) عكس عقاربِ الساعةِ أو (°180 مع عقاربِ الساعةِ):

$\mathbf{(}\mathbf{a}\mathbf{,}\mathbf{ }\mathbf{b}\mathbf{)}\mathbf{ }\mathbf{\to }\mathbf{ }\mathbf{(}\mathbf{-}\mathbf{a}\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{b}\mathbf{)}$

• الدورانُ بزاويةِ (°270) عكس عقاربِ الساعةِ أو (°90 مع عقاربِ الساعةِ):

 $\mathbf{(}\mathbf{a}\mathbf{,}\mathbf{ }\mathbf{b}\mathbf{)}\mathbf{ }\mathbf{\to }\mathbf{ }\mathbf{(}\mathbf{b}\mathbf{,}\mathbf{ }\mathbf{-}\mathbf{a}\mathbf{)}$

 

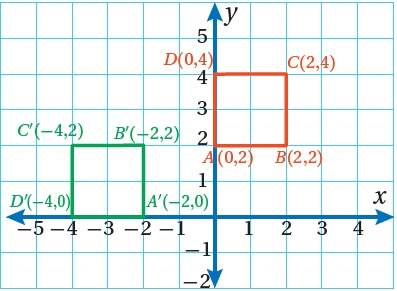
مثال 2: أرسمُ في المستوى الإحداثيِّ المربّعَ الذي إحداثياتُ رؤوسِهِ $\mathbf{A}\mathbf{(}\mathbf{0}\mathbf{,}\mathbf{2}\mathbf{)}\mathbf{,}\mathbf{ }\mathbf{B}\mathbf{(}\mathbf{2}\mathbf{,}\mathbf{2}\mathbf{)}\mathbf{,}\mathbf{ }\mathbf{C}\mathbf{(}\mathbf{2}\mathbf{,}\mathbf{4}\mathbf{)}\mathbf{,}\mathbf{ }\mathbf{D}\mathbf{(}\mathbf{0}\mathbf{,}\mathbf{4}\mathbf{)}$ ، ثمَّ أجدُ صورَتَهُ تحتَ تأثيرِ: 

1) دورانٍ مركزُهُ نقطةُ الأصلِ بزاويةِ ° 270 مع عقاربِ الساعةِ.

أبدِّلُ موقعَ الإحداثيّاتِ (x,y) ثمَّ أضرِبُ y في 1-

(−y , x)	(x , y)
A' (−2, 0)	A (0, 2)
B ' (−2, 2)	B (2, 2)
C ' (−4, 2)	C (2, 4)
D' (−4, 0)	D (0, 4)

 

يكونُ الشكلُ ذا تماثلٍ دورانيٍّ (Rotational symmetry) إذا عادَ إلى وضعِهِ الأصليِّ مرَّتيْنِ أوْ أكثرَ في أثناءِ تدويرِهِ بزاويةِ(°360) (دورةٌ كاملةٌ) حولَ مركزِهِ. 

تُعرَّفُ رتبةُ التماثلِ الدورانيِّ (Order of rotational symmetry): بأنَّها عددُ المرّاتِ التي يعودُ فيها الشكلُ ذو التماثلِ الدورانيِّ إلى وضعِهِ الأصليِّ خلالَ دورةٍ كاملةٍ حولَ مركزِهِ.

مثال 3: أُحدِّدُ إذا كانَ الشكلُ ذا تماثلٍ دورانيٍّ أمْ لا، ثمَّ أُحدِّدُ رتبةَ الدورانِ (إنْ وُجِدَتْ) في كلٍّ ممّا يأتي:

1)  

 

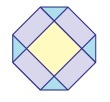
الشكلُ ذو تماثلٍ دورانيٍّ؛ لأنَّهُ يعودُ إلى وضعِهِ الأصليِّ أربعَ مرّاتٍ عندَ تدويرِهِ بزاويةِ (° 360) حولَ مركزِهِ. إذنْ، رتبةُ التماثلِ الدورانيِّ هيَ 4

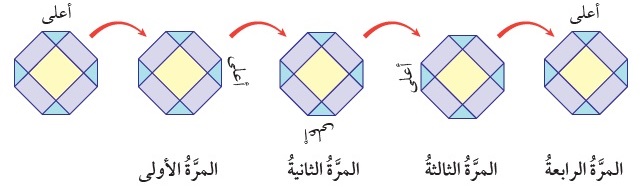
2)

الشكلُ ليسَ ذا تماثلٍ دورانيٍّ؛ لأنَّهُ يعودُ إلى وضعِهِ الأصليِّ مرَّةً واحدةً فقطْ عندَ  تدويرِهِ بزاويةِ (° 360) حولَ مركزِهِ

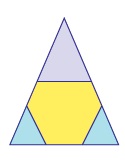
3)

الشكلُ ذو تماثلٍ دورانيٍّ؛ لأنَّهُ يعودُ إلى وضعِهِ الأصليِّ ثلاث مرّاتٍ عندَ تدويرِهِ بزاويةِ (° 360) حولَ مركزِهِ. إذنْ، رتبةُ التماثلِ الدورانيِّ هيَ3