العامل المشترك الأكبر
فكرة الدرس : أجد العامل المشترك الأكبر لعددين .
* تسمى العوامل التي يشترك فيها عددان أو أكثر بالعوامل المشتركة (Common factors) ويسمى أكبر هذه العوامل بالعامل المشترك الأكبر (Greatest common factor) ويرمز له بالرمز ( ع.م.أ ) .
مثال :
عوامل العدد 60 : 1 , 2 , 3 , 4, 5, 6 , 10, 12, 15, 20, 30, 60.
عوامل العدد 36 : 1 ,2, 3 ,4, 6, 9, 12, 18 , 36 .
ألاحظ أن العوامل المشتركة بين العددين هي : 1, 2, 3, 4, 6, 12 وأن العامل المشترك الأكبر لهما هو 12 .
مثال1 : أجد العامل المشترك الأكبر للعددين 35 و 40 .
الجواب :
| عوامل العدد 40 |
خطوات الحل : 1- أجد عوامل العددين . 2- أحدد العوامل المشتركة للعددين . 3- اختار أكبر عامل مشترك بينهما . |
عوامل العدد 35 |
| 1×40 | 1× 35 | |
| 2×20 | 5×7 | |
| 4×10 | ||
| 5×8 |
العوامل المشتركة بين العددين هي 1 , 5 لذلك فإن العامل المشترك الأكبر هو 5 .
ويمكنني أيضا أن أجد العامل المشترك الأكبر لعددين بطريقة أخرى تعتمد على التحليل الى العوامل الأولية التي تعلمتها في الدرس السابق ..
مثال2 : أجد العامل المشترك الأكبر للعددين 75 و 100 .
الجواب :
لإيجاد العامل المشترك الأكبر للعددين 75 و 100 باستعمال التحليل الى العوامل الأولية اتبع الخطوات الاتية :
الخطوة 1 : أحلل العددين 75 و 100 الى عواملها الأولية .
 |
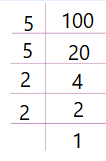 |
الخطوة 2 : أحدد العوامل الأولية المشتركة .
الخطوة 3 : أجد ع.م.أ للعددين بضرب العوامل الأولية المشتركة ( نأخذ عاملا واحد من كل عاملين أوليين متساويين ) .
اذن ع.م.أ للعددين 100 و 75 هو 25.
مثال3 : أعد صالح افطار لعدد من الصائمين , فوزع 18 علبة تمر و 24 كوب ماء على عدد من الصناديق بحيث تحتوي الصناديق جميعها على عدد متساو من علب التمر وعدد متساو من أكواب الماء . فما أكبر عدد من الصناديق يمكن أن يجهزها .
الجواب :
لايجاد أكبر عدد من الصناديق التي يمكن أن يجهزها نجد العامل المشترك الأكبر للعددين 18 و 24 .
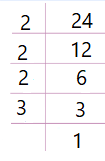 |
 |
أحدد العوامل المشتركة :
اذن العامل المشترك الأكبر = 3 ×2 = 6 .
يمكن أن يجهز 6 صناديق .