رياضيات فصل أول

 تساعدُ بعضُ الأزواجِ الخاصةِ منَ الزوايا على إيجادِ قياساتِ زوايا مجهولةٍ.

مفهوم أساسي:

الزاويتانِ المُتجاوِرتانِ (Adjacent angles): هما زاويتان لهُما الرأسُ نفسُهُ، ولهُما ضِلْعٌ مُشترَكٌ، لكنَّهُما لا تتداخلانِ. 

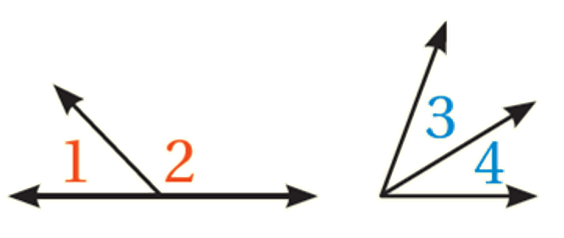
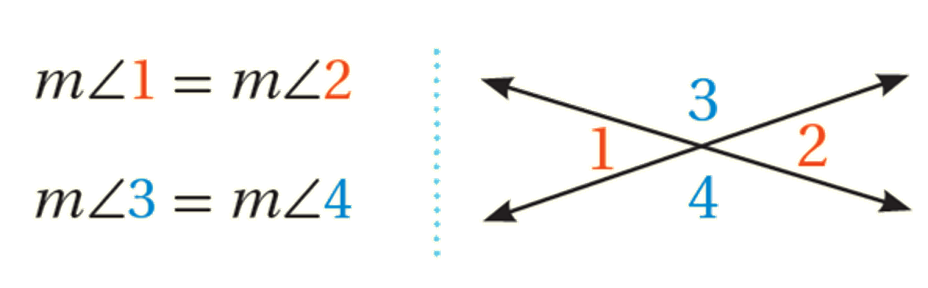
الزاويتانِ المُتقابِلتانِ بالرأسِ (vertical angle): هما زاويتان مُتقابِلتانِ تَنتُجانِ منْ تقاطعِ مستقيميْنِ. وكلُّ زاويتيْنِ مُتقابِلتيْنِ بالرأسِ لهُما القياسُ نفسُهُ. 

الزاويتانِ المُتتامَّتانِ (Complementary angles):  هما زاويتان مجموعُ قياسَيْهِما $90°$

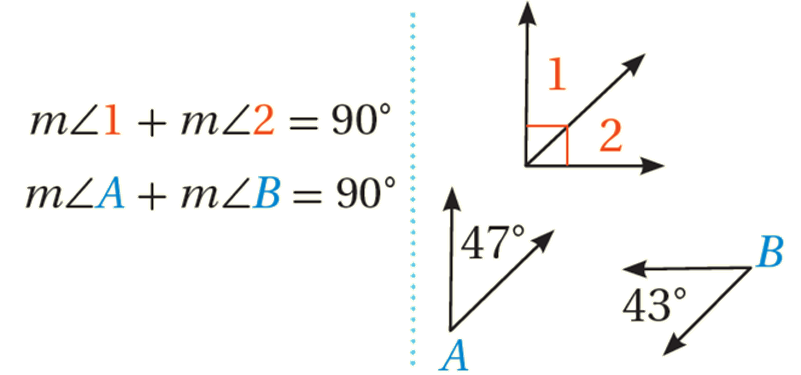
الزاويتانِ المُتكامِلتانِ (Supplementary angles):  هما زاويتان مجموعُ قياسَيْهِما $180°$

 

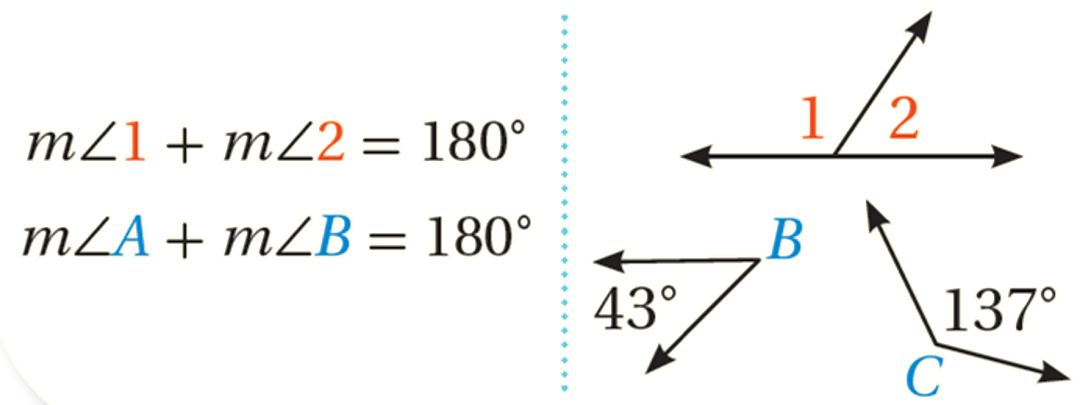
مثال 1: اعتمادًا على الشكلِ المجاورِ، أُسَمّي: 

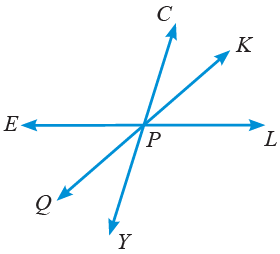
1) زاويتينِ متقابلتَيْنِ بالرأسِ:

$\angle \mathrm{CPK}, \angle \mathrm{QPY}$ لأنَّهُما نَتَجَتا منْ تقاطعِ المستقيمينِ $\overleftrightarrow{\mathrm{QK}} , \overleftrightarrow{\mathrm{CY}}$ 

2) زاويتينِ مُتكامِلَتَيْنِ:

$\angle \mathrm{CPE}, \angle \mathrm{CPL}$ لأنَّ مجموعَ قياسَيْهِما ° 180 ، وهما تشكِّلانِ زاويةً مستقيمةً.

3) زاويتينِ مُتجاورتيْنِ:

$\angle \mathrm{KPL}, \angle \mathrm{LPY}$ لأنَّ لهُما رأسًا مشترَكًا (P)  وضلعًا مشترَكًا $\overleftrightarrow{\mathrm{PL}}$ ولا تَتَداخلانِ. 

 

يمكنُ استخدامُ العلاقاتِ بينَ الزوايا والمعادلاتِ في إيجادِ قياساتِ زوايا مجهولةٍ. 

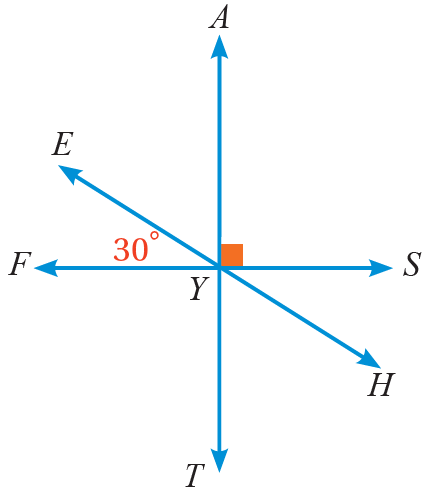
مثال 2: أستخدمُ الشكلَ المجاورَ لإيجادِ قيمةِ كلٍّ ممّا يأتي:

1) $\mathbf{m}\mathbf{\angle }\mathbf{SYH}$

زاويتانِ متقابلتانِ بالرأسِ                            $$\begin{gathered} \mathrm{m}\angle \mathrm{SYH}=\mathrm{m}\angle \mathrm{EYF} \\ \mathrm{m}\angle \mathrm{SYH}=30° \end{gathered}$$                              

2) $\mathbf{m}\mathbf{\angle }\mathbf{AYE}$

زوايا متجاورةٌ على مستقيمٍ                   $\mathrm{m}\angle \mathrm{SYA}+\mathrm{m}\angle \mathrm{AYE}+\mathrm{m}\angle \mathrm{EYF}=180°$                         

أعوض                                                    $90°+\mathrm{m}\angle \mathrm{AYE}+30°=180°$                                         

أجد الناتج                                                 $$\begin{gathered} \mathrm{m}\angle \mathrm{AYE}+120°=180° \\ \mathrm{m}\angle \mathrm{AYE}=60° \end{gathered}$$                                                   

 

مثال 3: منَ الحياةِ :أجدُ قيمةَ y في الشكلِ المجاورِ. 

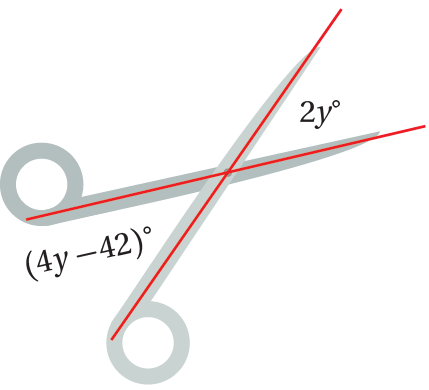
بما أنَّ العبارتيْنِ الجبريَّتيْنِ هُما قياسا زاويتينِ متقابلتيْنِ بالرأسِ،

فإنَّهُ يمكنُ كتابةُ المعادلةِ الآتيةِ:

                                                                $4\mathrm{y}-42=2\mathrm{y}$                                     

أطرح 4y من الطرفين                               $-42=-2\mathrm{y}$                                                                 

أقسم على 2-                                             $21=\mathrm{y}$