العَشَرات
تهيئة:
أَتَأمّل مجموعتي الأعداد ثُمَّ أٌقارن:
المجموعة (1)
المجموعة (2)
كم عد المنازل في المجموعة الأولى؟
كم عد المنازل في المجموعة الثانية؟
ما الاختلاف الذي حصل للأعداد في المجموعة الثانية؟
أقارِنُ إجابتي بالإجابة الآتية:
كم عد المنازل في المجموعة الأولى؟ عدد المنازل في المجموعة الأولى هُوَ منزلة واحدة.
كم عد المنازل في المجموعة الثانية؟ عدد المنازل في المجموعة الثانية هُوَ منزلتين.
ما الاختلاف الذي حصل للأعداد في المجموعة الثانية؟ الاختلاف الذي حصل للأعداد في المجموعة الثانية هُوَ أننا قمنا بإضافة العدد (0) أمام الأعداد، وبذلك يتغير اسم العدد، حيث أنّ العدد (1) مثلًا أصبح في المنزلة الثانية والتي نسميها منزلة العشرات، بينما العدد (0) أصبح في منزلة الآحاد. وبذلك يصبح العدد الجديد الذي تشكل لدينا هُو (10) عَشَرَة.
ما وَجْهُ التَّشابُهِ بَيْنَ الْأَعْدادِ الْآتِيَةِ جَميعِها؟
أقارِنُ إجابتي بالإجابة الآتية:
ألاحظ أنّ وجه التشابه بين الأعداد هُو أنّ آحادها (0) أي أنّ المنزلة الأولى فيها هُوَ (0).

أتأمل المثال الآتي:
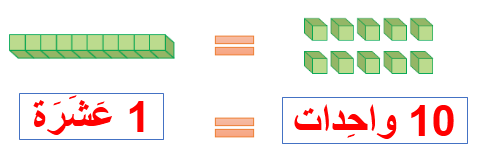
أستطيعُ أن أَجْمَعُ كُلَّ 10 واحِداتٍ لِأَحْصُلَ عَلى 1 عَشَرَةٍ.
ألاحظ أنّ عَدد المكعبات في المجموعة الأولى هو (10)،
كما ألاحظ أنّ عدد المكعبات في المجموعة الثانية هُوَ (10) لكن تمّ جمعها في عامود واحد ليسهل علينا عدها.
والآن أعدّ أعمدة المكعبات الآتية:
ألاحظ أنّ عَدد أعمدة المُكعبات هُوَ (5) أعمدة، وكلّ عامود يحوي (10) مكعبات صغيرة.
 يمكنني الآن عدّ الأعمدة ووضع أمامها (0) لأحصل على عدد المكعبات.
يمكنني الآن عدّ الأعمدة ووضع أمامها (0) لأحصل على عدد المكعبات.
عدد الأعمدة = 5
كل عامود يحوي 10 مكعبات، أي 10 وَ 10 وَ 10 وَ 10 وَ 10 = 50
كما يمكنني القول 5 أعمدة = 50 مُكعب.
نَشاط (1)
أعدّ أعمدة المكعبات الآتية:
كم عَدد المكعبات  ؟
؟
أقارِنُ إجابتي بالإجابة الآتية:
4 أعمدة عَشَرات = 40 أربعون.
أَتَحَدَّثُ: كَيْفَ أُحَدِّدُ عَدَدَ الْعَشَراتِ في 70 مُكَعَّبًا؟
أقارِنُ إجابتي بالإجابة الآتية:
أستطيع تحديد عدد العشرات في 70 مكعبا من خلال وضع كل 10 مكعبات في عامود واحد، ثُمَّ أقوم بعد الأعمدة.
7 أعمدة عَشَرات = 70 سبعون.