رياضيات فصل أول

الدرس الثاني: القسمة كطرح متكرر

تمهيد 

إشارة القسمة هي $÷$

أستكشف 

قِطْعَةُ قُماشٍ طولُها 18 m ، إِذا قَسَّمَها الْبائِعُ إِلى 9 قِطَعٍ مُتَساوِيَةِ الطّولِ، فَما طولُ كُلِّ قِطْعَةٍ؟ 

تعلمنا في الدرس السابق إيجاد نناتج القسمة كمجموعات متساوية وقسمة بالتساوي.

سوف نتعلم في هذا الدرس طريقة جديدة للقسمة وهي الطرح المتكرر.

أتعلم 

  يُمْكِنُني إيجادُ ناتِجِ الْقِسْمَةِ بِاسْتِعْمالِ الطَّرْحِ الْمُتَكَرِّرِ عَلى خَطِّ الْأَعْدادِ، وَذلِكَ بِطَرْحِ الْعَدَدِ نَفْسِهِ مَرَّةً بَعْدَ مَرَّةٍ حَتّى أَصِلَ إِلى الصِّفْر

•إذا قَسَّمْتُ 12 قِطْعَةَ عَدٍّ إِلى 3 مَجْموعاتٍ مُتَساوِيَةٍ، فَكَمْ قِطْعَةَ عَدٍّ في كُلِّ مَجْموعَةٍ؟

الحل:

لِأَجِدَ عَدَدَ قِطَعِ الْعَدِّ في كُلِّ مَجْموعَةٍ فَإِنَّني أَجِدُ ناتِجَ: 12 ÷ 3

• أَسْتَعْمِلُ الطَّرْحَ الْمُتَكَرِّرَ عَلى خَطِّ الأَعْدادِ، فَأَبْدَأُ مِنَ الْعَدَدِ 12 ، وَأَطْرَحُ 3 في كُلِّ مَرَّةٍ حَتّى أَصِلَ إِلى الصِّفْرِ.

ألاحظ في خط الأعداد أنني بدأت من العدد المراد قسمته 12

في كل مرة أقفز يكون طول القفزة بمقدار المقسوم عليه (3)

الناتج سيكون هو عدد القفزات المجموعات.(4)

أُلاحِظُ أَنَّني طَرَحْتُ 3 قِطْعِ عَدٍّ 4 مَرّاتٍ، إِذَنْ:

 

 

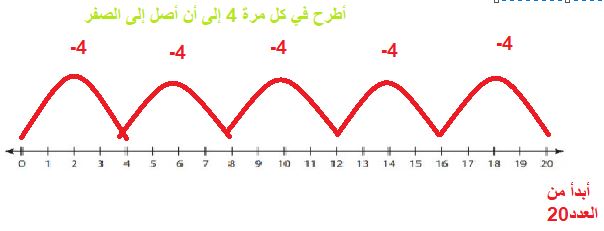
أَتَحَدَّثُ: كَيْفَ أَسْتَعْمِلُ الطَّرْحَ الْمُتَكَرِّرَ عَلى خَطِّ الْأَعْدادِ لِأَجِدَ ناتِجَ 20 ÷ 4 ؟

              •لأجِدَ ناتِجَ القسمة بِاسْتِعْمالِ الطَّرْحِ الْمُتَكَرِّرِ عَلى خَطِّ الْأَعْدادِ، وَذلِكَ بِطَرْحِ الْعَدَدِ نَفْسِهِ مَرَّةً بَعْدَ مَرَّةٍ حَتّى أَصِلَ إِلى الصِّفْر.

ألاحظ في خط الأعداد أنني بدأت من العدد المراد قسمته 20

في كل مرة أقفز يكون طول القفزة بمقدار المقسوم عليه (4)

الناتج سيكون هو عدد القفزات المجموعات.(5)

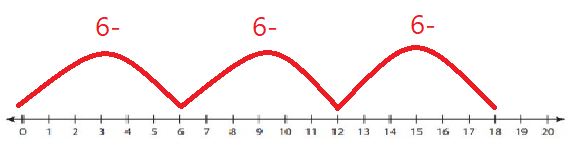
مثال إضافي للتوضيح: أجد ناتج قسمة $= 6 ÷18$

:              •لأجِدَ ناتِجَ القسمة بِاسْتِعْمالِ الطَّرْحِ الْمُتَكَرِّرِ عَلى خَطِّ الْأَعْدادِ، وَذلِكَ بِطَرْحِ الْعَدَدِ نَفْسِهِ مَرَّةً بَعْدَ مَرَّةٍ حَتّى أَصِلَ إِلى الصِّفْر.

ألاحظ في خط الأعداد أنني بدأت من العدد المراد قسمته 18

في كل مرة أقفز / أطرح يكون طول القفزة بمقدار المقسوم عليه (6)

الناتج سيكون هو عدد القفزات المجموعات.(3)

إذن $3 = 6 ÷ 18$،