القياسُ Measurement
القياسُ مهارةٌ لا يقتصرُ استخدامُها في مجالِ العلومِ فقطْ، بلْ يُستخدمُ

القياسُ في مجالاتِ الحياةِ المختلفةِ؛  حيث إنَّ التعبيرَ عنِ الكميّاتِ بالأرقامِ،

أكثرُ دقّةً منَ الاعتمادِ على الوصفِ النظريِّ. فوصفُ درجةِ حرارةِ الجسمِ بأنَّها

 «مرتفعةٌ » لا يكونُ دقيقًا إذا ما قورِنَ بالوصفِ الرقميِّ بالقولِ إنَّ درجةَ حرارةِ

الجسمِ  $39 C°$، والطبيبُ لنْ يتمكّنَ منْ تشخيصِ حالةِ المريضِ على نحوٍ دقيقٍ

 قبلَ أنْ يطلبَ فحوصًا تتضمنُ

إجراءَ قياساتٍ لدرجةِ الحرارةِ، ومعدلِ ضرباتِ القلبِ، وضغطِ الدمِ، وغيرِها.

يمكنُ تعريفُ القياسِ Measurement بأنَّهُ وسيلةٌ للتعبيرِ بالأرقامِ عنْ كميّةٍ

فيزيائيّةٍ، عنْ طريقِ مقارنتِها بكميّةٍ معلومةٍ منَ النوعِ نفسِه تُسمَّى وَحدةَ

 القياسِ، مثلُ قياسٍ طول قلمٍ بوحدةٍ (cm). أو قياسِ درجةِ حرارةِ الغرفةِ

بوحدةِ درجةِ سلسيوس ( ˚C ).

وتتضمّنُ عمليةُ القياسِ ثلاثةَ عناصرَ رئيسةٍ هيَ:

• الكميّةُ الفيزيائيّةُ المرادُ قياسُها،
• أداةُ القياسِ،
• وحدةُ القياسِ.

ويبيّنُ الشكلُ ( 2) أحدَ أشكالِ الموازينِ المستخدمَ في الحياةِ اليوميّةِ لقياسِ الكتلةِ.

الشكل ( 2): عناصرُ القياسِ.

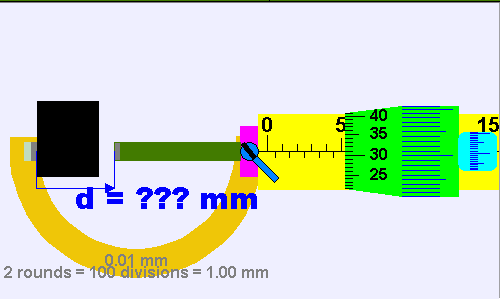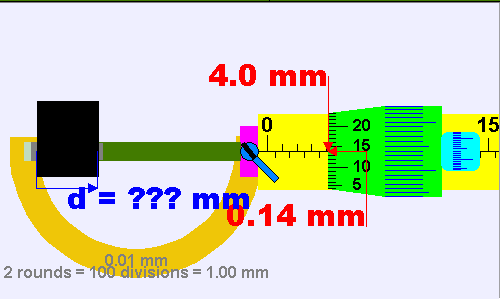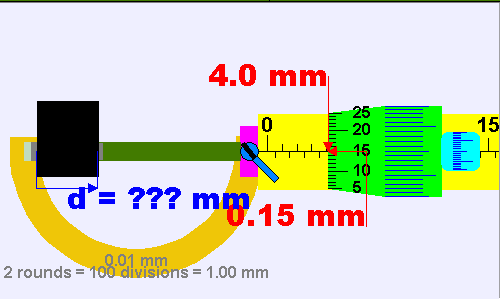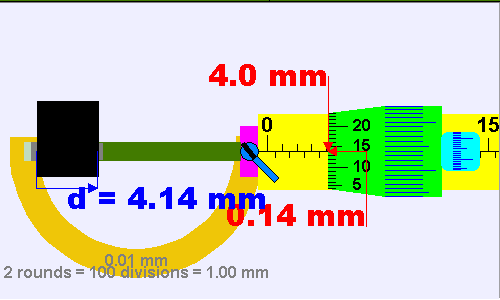
أدواتُ القياسِ Measuring

تتنوّعُ أدواتُ القياسِ في أشكالِها؛ لتُناسبَ الغرضَ الذي صُمِّمتْ منْ أجلِه، ومنَ

الأمورِ الواجبِ أخذُها في الحسبانِ في عمليّةِ القياسِ:

اختيارُ الأداةِ المناسبةِ، ومعرفةُ أصغرِ تدريجٍ يقرؤُه الجهازُ أو الأداةُ. فمثلًا،

الطولُ كميّةٌ فيزيائيّةٌ يمكنُ قياسُها بأدواتٍ مختلفةٍ، منها المِسطرةُ؛ وهي من

أبسطِ أدواتِ القياسِ المُستخدَمةِ في الحياةِ اليوميّةِ. هذهِ الأداةُ عادةً تكونُ مدرَّجةً

بالمليمترِ، وأصغرُ تدريجٍ يظهرُ على المِسطرةِ ( $1 mm$ ). وقد تكونُ المسطرةُ مناسبةً

لقياسِ طولِ قلمٍ أو كتابٍ، لكنْ لا يمكنُ أنْ تكونَ أداةً مناسبةً لقياسِ سُمْكِ ورقةٍ أو

صفيحةٍ رقيقةٍ. ويبيّنُ الشكلُ ( 3) أداةً تُسمَّى الميكروميتر، تصلُ دقّةُ القياسِ فيها

إلى ( $0.01 mm$ )، ويمكنُ استخدامُها في قياسِ سُمكِ صفيحةٍ رقيقةٍ. أتأمّلُ الشكلَ ( 4)،

وأتعرّفُ كيفيّةَ تسجيلِ قراءةِ الميكروميتر مُتّبعًا الخطواتِ الآتيةَ:

1-أسجّلُ قراءةَ المقياسِ الطوليِّ العلويِّ ويكونُ بالمليمتر ( 7.0mm ).

2-أسجّلُ قراءةَ المقياسِ الطوليِّ السفليِّ ويكونُ بأنصافِ المليمتر .(0.5mm)

3-أسجّلُ قراءةَ التدريجِ الدائريِّ بقراءةِ التدريجِ المنطبقِ على المقياسِ الطوليّ ( 24 )، وضربه

بقيمة المنزلة التي يمثلها التدريجٍ الدائريٍّ وهي ( 0.01 ) فتكون القراءة ( $0.24 mm$).

 4-أجمعُ القراءاتِ الثلاثَ فتمثّلُ قراءةَ الميكروميتر.

الشكل ( 3): قياسُ سُمْكِ صفيحةٍ 

باستخدامِ الميكروميتر.

الشكل ( 4): حسابُ قراءةِ 

   الميكروميتر بوحدةِ (m)

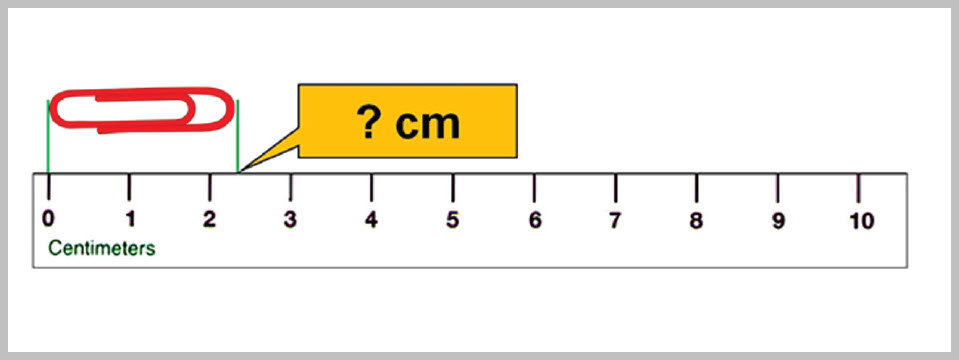
الأرقامُ المحدّدةُ والأرقامُ المعنويةُ Exact Numbers and Significant Figures

يستخدمُ الفيزيائيونَ الأرقامَ بطرائقَ مختلفةٍ. فقد تُستخدمُ الأرقامُ في عدِّ الأشياءِ،

 على نحوِ ما هو مُبيَّنٌ في الشكلِ ( 5)، حيثُ يظهرُ في الصورةِ ( 5) كتبٍ، وهذا الرقمُ

 محدَّدٌ Exact Number لا مجالَ للشكِّ فيهِ، فلا يمكنُ لأحدٍ أنْ يقولَ إنَّ عددَ الكتبِ

 ربَّما يكونُ ( 5.45 ) أو ( 5.5 ) كتابٍ مثلًا. وقد تُستخدمُ الأرقامُ في التعبيرِ عنِ العلاقةِ

بينَ وَحدتينِ من وَحداتِ القياسِ، فمثلً منَ المعلومِ أنَّ المترَ ( $1 m$ ) يساوي ( $100 cm$ )، 

وأنَّ الساعةَ ($1 hour$) تساوي ( $60 min$ )، وفي هذهِ الحالةِ أيضًا، فإنَّ الأرقامَ المُستخدَمةَ

تكونُ ذاتَ قيمةٍ محدّدةٍ وثابتةٍ.

وتُستخدمُ الأرقام أيضًا في التعبيرِ عنْ نتائجِ القياساتِ، وفي عمليةِ القياسِ لا يمكنُ

 الحصولُ على نتيجةٍ مؤكَّدةٍ تمامًا؛ فالقياسُ لا يعطي قيمةً محدّدةً تعبّرُ تمامًا عنِ

 القيمةِ الحقيقيّةِ. فمثلاً يبيّنُ الشكلُ ( 6) مِسطرةً مدرَّجةً بوحدةِ السنتيمتر؛ أيْ إنَّ

 أصغرَ تدريجٍ يظهرُ على المسطرةِ ($1 cm$)، فالمسطرةُ استُخدِمتْ لقياسِ طولِ

 مشبكِ ورقٍ، وعلى نحوِ ما يظهرُ  في الشكلِ، فإنَّهُ منَ المؤكَّدِ أنَّ طولَ المِشبكِ

 أكبرُ منْ ( $2 cm$ )، فإذا طُلِبَ إلى شخصينِ  تسجيلُ طولِ المِشبكِ، فقدْ يُقدِّرُ أحدُهما

 أنَّهُ  (2.3cm، في حينِ قد يُقدّرُ الآخرُ بأنَّهُ ($2.4 cm$). ومنَ المُلاحَظِ أنَّ نتيجةَ القياسِ

 تضمّنَتْ رقمًا مؤكّدًا قُرِئَ منْ تدريجِ المسطرةِ مباشرةً وهو ($2 cm$).ورقمًا تقديريًّا

 مشكوكًا فيه وهو ( 0.3 )، أو ( 0.4 ) اختُلِفَ في تقديرُه منْ شخصٍ إلى آخرَ.

الشكل ( 5): يظهرُ في الصورةِ

 عددٌ محدَّدٌ منَ الكتبِ وهو (5) كتبٍ.

الشكل ( 6): قياسُ طولِ مشبكٍ باستخدامِ مسطرةٍ مدرجةٍ بالسنتيمتر.

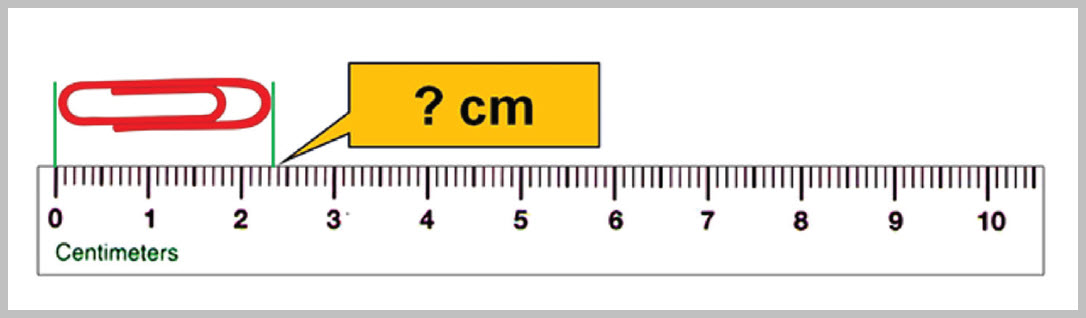
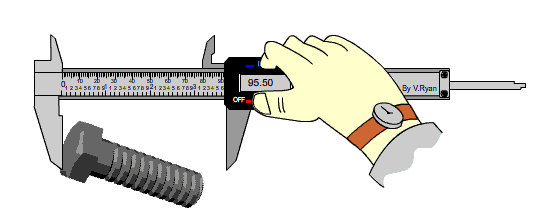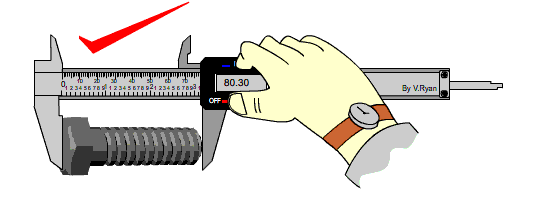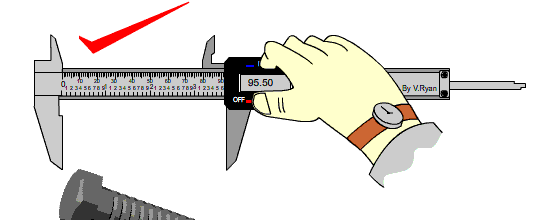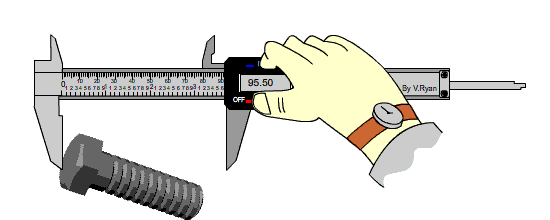
 يطلق على الأرقام المؤكدة إضافة إلى الرقم التقديري التي تنتج عن عملية القياس

 بالأرقام المعنوية Significant Figures .وهذا يعني أن قياس طول مشبك الورقِ 

باستخدامِ المسطرةِ المبينةِ في الشكلِ ( 6) يتضمّنُ رقمينِ معنويينِ.

يعتمدُ عددُ الأرقامِ المعنويّةِ في القياسِ على مقدارِ أصغرِ تدريجٍ يظهرُ على أداةِ القياسِ.

فالمِسطرةُ المُبيَّنةُ في الشكلِ ( 7) مدرَّجةٌ بأجزاءِ السنتيمترِ (المليمترات)، لذا فإنَّ 

استخدامَها في قياسِ طولِ مِشْبكِ الورقِ نفسِه يُعطي قياسًا أكثرَ دقةً، فالمِسطرةُ

تؤكّدُ رقمينِ هما ( 2.3cm )، وتسمحُ بتقديرِ أجزاءِ المليمترِ، إذْ يمكنُ تقديرُ أنَّ طولَ

 المِشبكِ ( 2.33cm ) أو ( 2.34cm )، وفي هذهِ الحالةِ فإنَّ القياسَ يتضمّنُ (3) أرقامٍ 

 معنويّةٍ؛رقمينِ مؤكَّدينِ، ورقمًا مشكوكًا فيهِ. وبوجهٍ عامٍّ، يكونُ الرقمُ الأبعدُ إلى اليمينِ

 في نتيجةِ القياسِ مشكوكًا فيهِ، ولا يمكنُ تأكيدُه إلا باستخدامِ أداةِ قياسٍ أخرى أكثرَ دقّةً.

 وكلّما زادَ عددُ الأرقامِ المعنويّةِ زادتْ دقّةُ القياسِ.

الشكل (7): قياسُ طولِ مِشبكٍ باستخدامِ مسطرةٍ مُدرَّجةٍ بأجزاءِ السنتيمتر.

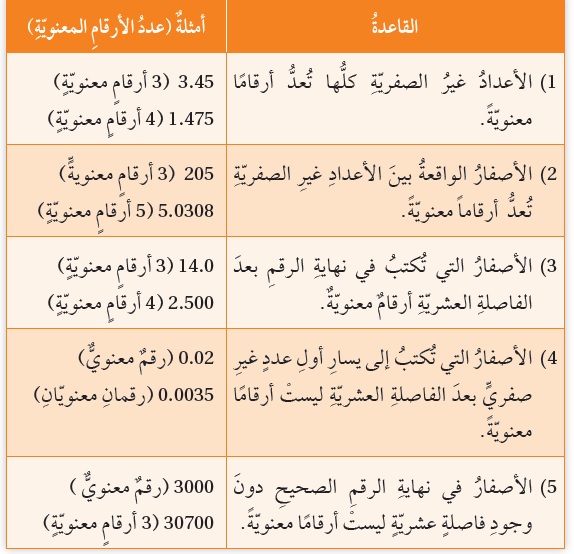
قواعدُ التعامُلِ معَ الأرقامِ المعنويّةِ Rules for dealing with significant figures

 تُعَدُّ جميعُ الأرقامِ غيرِ الصفريّةِ التي تظهُر في القياسِ أرقامًا معنويّةً، أمّا الصفرُ فربَّما

 يكونُ معنويًّا أو غيرَ معنويٍّ. فمثلاً يُبيّنُ الشكلُ ( 8) مقطعًا من مخبارٍ مدرَّجٍ بوحدةِ

 مللتر ( mL )،فإذا كانَ ارتفاعُ الماءِ في المخبارِ ينطبقُ تمامًا عندَ التدريجِ ( 37 )، فعندئذٍ

 يمكنُ التعبيرُ عنِ القياسِ بالصورة (37.0ml)، وحينئذٍ يُعَدُّ الصفرُ رقمًا معنويًّا. أمّا

 الأصفارُ المُستخدَمةُ في تحديدِ موقعِ الفاصلةِ العشريةِ فلا تُعدُّ أرقامًا معنويّةً، كما

 في القياسِ ( 0.003 ) الذي يحتوي على رقمٍ معنويٍّ واحدٍ فقطْ. ولتجنُّبِ الوقوعِ في

 الخطأِ في حالةِ الأصفارِ في نهايةِ الرقمِ الصحيحِ، يُكتبُ القياسُ بالصورةِ العلميّةِ،

فمثلً عندَ كتابةِ القياسِ ( 3000 ) بالصورةِ ($3 x {10}^3$) سيبدو واضحًا أنَّ القياسَ

 يحتوي على رقمٍ معنويٍّ واحدٍ. أمّا إذا كُتبَ القياسُ على الصورةِ ( $3.0 x {10}^3$ )،

 فسيكونُ فيهِ رقمانِ معنويّانِ، وهذا يدلُّ على أنَّ أداةَ القياسِ المُستخدَمةَ في

 الحالةِ الثانيةِ أكثرُ دقّةً. والجدولُ الآتي يوضّحُ القواعدَ الواجبَ العملُ بمقتضاها

 عندَ تحديدِ عددِ  الأرقامِ المعنويّةِ  في القياسِ.

الشكل ( 8): قياسُ الحجمِ 

 باستخدامِ المخبارِ المدرَّجِ.

 أربعة أرقام  معنوية(

 خمسة أرقام معنوية

 خمسة أرقام  معنوية

  ثلاثة أرقام  معنوية

مثال محلول

قاسَ طالبٌ طولَ قلمٍ مستخدمًا مسطرةً، وعبّرَ عنْ نتيجةِ القياسِ بأنَّهُ ( $10.35 cm$).

أجيبُ عنِ الأسئلةِالآتيةِ:
أ . ما أصغرُ تدريجٍ يظهرُ على المسطرةِ التي استخدمَها الطالبُ؟
ب . ماعددُ الأرقامِ المعنويّةِ في القياسِ الذي كتبَهُ الطالبُ؟

الحل

أ . يمكنُ معرفةُ أصغرِ تدريجٍ للمسطرةِ منْ آخرِ رقمٍ مؤكَّدٍ سجّلَه 
       

 ألاحظُ أنَّ آخِرَ رقمٍ مؤكَّدٍ في القياسِ هو الرقمُ (3)، ويقعُ في منزلةِ جزء من العشرة،  أيْ أنَّ

 أصغرَ تدريجٍ للمسطرةِ هو ( $0.1 cm$ )، ويساوي ( $1 mm$ ).

 ب . عددُ الأرقامِ المعنويّةِ ( 4).

تمرين

أُحدّدُ عددَ الأرقامِ المعنويّةِ في كلٍّ منَ القياساتِ الآتيةِ:
أ . $202 mm$
ب . $1.250 \mathrm{cm}$
ج. $0.050 mL$

د .  $6.01x{10}^{-3}m$

إجراءُ العمليّاتِ الحسابيّةِ باستخدامِ الأرقامِ المعنويّةِ 

 Significant Figures in Calculations

عندَ إجراءِ العمليّاتِ الحسابيّةِ باستخدامِ الأرقامِ المعنويّةِ، يجبُ العملُ بمقتضى

 القواعدِ الآتيةِ:

   1. الجمعُ والطرحُ: أتّبعُ الخطواتِ المبيَّنةَ في المثالِ الآتي:

          - أحدّدُ عددَ المنازلِ العشريّةِ (بعدَ الفاصلةِ) للكميّاتِ المطلوبِ جمعُها أو طرحُها:

2. الضربُ والقسمةُ: أتّبعُ الخطواتِ المبيَّنةَ في المثالِ الآتي:

   - أحدّدُ عددَ الأرقامِ المعنويّةِ في الكميّاتِ المعطاةِ.

   - أحسُبُ ناتجَ عمليّةِ الضربِ أو القسمةِ، وأُدوِّرُ الناتجَ ليكونَ عددُ الأرقامِ المعنويّةِ فيهِ

      مساويًا  لعددِ الأرقامِ في القياسِ الذي يشتملُ على العددِ الأقلِّ منَ الأرقامِ المعنويّةِ .

- أتّبعُ القاعدةَ التي تعلّمْتُها في الرياضياتِ لتدويرِ الأرقامِ.

3. إجراءُ العمليّاتِ الحسابيّةِ باستخدامِ الآلةِ الحاسبةِ:
عندَ إجراءِ العمليّاتِ الحسابيّةِ باستخدامِ الآلةِ الحاسبةِ، فإنَّ الإجابةَ قد لا تحتوي على العددِ الصحيحِ

من الأرقامِ المعنويّةِ، لذا تُستخدمُ القواعدُ السابقةُ نفسُها في تدويرِ الإجابةِ إلى العددِ الصحيحِ منَ 

الأرقامِ المعنويّةِ، على نحوِ ما يتضحُ في المثالِ الآتي:

 عندَ استخدامِ الآلةِ الحاسبةِ فإنَّ الإجابةَ تساوي ( 2085.5688 )، لذا يلزمُ تدويرُ الإجابةِ إلى

  (5) أرقامٍ معنويّةٍ، فتكونُ الإجابةُ النهائيّةُ ( 2085.6 )

مثال محلول

    أجدُ ناتجَ الطرحِ، وأعبّرُ عنِ النتيجةِ بالعددِ المناسبِ منَ الأرقامِ المعنويّةِ وبالصيغةِ

    العلميّةِ :

    $2.38 \times {10}^3 cm – 19 cm$

   الحلُّ:
   الخطوةُ (1): كتابةُ العددينِ بالصيغةِ العلميّةِ على أنْ يكونَ لهما الأسُّ نفسُه.

   $2.38 \times {10}^3 cm – 0.019 \times {10}^3 cm$

 الخطوةُ (2): إيجادُ ناتجِ الطرحِ:

  $(2.38 - 0.019) \times {10}^3 = 2.361 \times {10}^3$
الخطوةُ (3): تدويرُ الجوابِ إلى عددِ المنازلِ العشريّةِ الأقلِّ في الكميّاتِ المُعطاةِ (منزلتين)،

والتعبيرُ عنِ الجوابِ بالصيغةِ العلميّةِ: $2.36 \times {10}^3 cm$

مثال محلول

قاستْ طالبةٌ أبعادَ قطعةَ كرتونٍ، فكانَ طولُها (24.1cm) وعرضُها (9.7cm). أحسُبُ

مِساحةَ القطعةِ مستخدمًا العددَ الصحيحَ منَ الأرقامِ المعنويّةِ.

الحلُّ:
الخطوةُ (1): أحسُبُ المِساحةَ باستخدامِ العلاقةِ:

                             $A = l \times w = 24.1 \times 9.7 = 233.77$

الخطوةُ (2): أكتبُ الإجابةَ بالصيغةِ العلميّةِ: $2.3377 \times {10}^2$

الخطوةُ (3): ألاحظُ أنَّ أقلَّ عددٍ منَ الأرقامِ المعنويةِّ في الكميّاتِ المعطاةِ هو رقمانِ، 

 وأدور الإجابة  إلى رقمينِ معنويّينِ، وأعبّرُ عنِ النتيجةِ بالصورةِ الآتيةِ $2.3 \times {10}^2 c{m}^2$