رياضيات11 فصل أول

القيم العظمى والصغرى لكثيرات الحدود

تزايد كثيرات الحدود وتناقصها:

بيانياً:

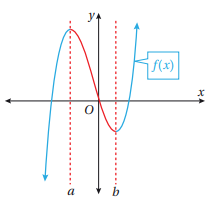
1) يكون الاقتران f(x) متزايداً إذا كان منحنى الاقتران يرتفع من اليسار إلى اليمين (تزداد قيمة y كلما زادت x)

2) يكون الاقتران f(x) متناقصاً إذا كان منحنى الاقتران ينخفض من اليسار إلى اليمين (تقل قيمة y كلما زادت x)

والشكل الآتي يوضح ذلك (التزايد باللون الأزرق والتناقص بالأحمر)

 

يكون الاقتران f متناقصا في الفترة I، إذا كان لكل $x_1<x_2$ في الفترة $f\left(x_1\right)>f\left(x_2\right)$ يكون الاقتران f متزايدا في الفترة I، إذا كان لكل $x_1<x_2$ في الفترة $f\left(x_1\right)<f\left(x_2\right)$.

ملاحظة: يمكننا استعمال المشتقة في دراسة تزايد وتناقص الاقتران f(x) 

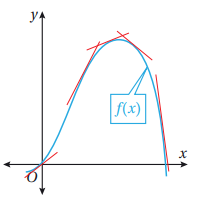
1) المماسات ذات الميل الموجب مرتبطة بالجزء المتزايد من منحنى الاقتران.

2) المماسات ذات الميل السالب مرتبطة بالجزء المتناقص من منحنى الاقتران.

وهذا يعني أننا يمكننا الاستفادة من إشارة المشتقة في تحديد فترات التزايد والتناقص.

 

إذا كان $f\text{'}\left(x\right)>0$ قيم x جميعها في الفترة I؛ فإن f يكون متزايدا على الفترة I. إذا كان $f\text{'}\left(x\right)<0$ لقيم x جميعها في الفترة I؛ فإن f يكون متناقصا على الفترة I.

 

النقاط الحرجة لكثيرات الحدود وأنواعها

النقطة الحرجة هي النقطة التي يمكن رسم مماس أفقي لكثير الحدود f(x) عندها (أي أن مشتقة الاقتران عندها تساوي صفرا) ويسمى الإحداثي x للنقطة الحرجة بالقيمة الحرجة.

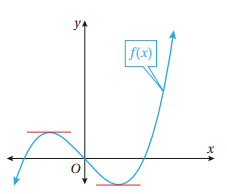
ملاحظة: يمكننا استعمال المشتقة لتصنيف النقاط الحرجة لكثيرات الحدود وتقسم إلى ثلاثة أشكال

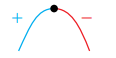
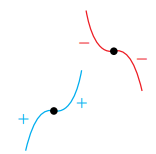
1) نقطة عظمى محلية: هي نقطة حرجة يكون منحنى الاقتران عن يسارها متزايدا وعن يمينها متناقصا (إشارة المشتقة تتغير من الموجب إلى السالب من اليمين إلى اليسار) 

2) نقطة صغرى محلية: هي نقطة حرجة يكون منحنى الاقتران عن يسارها متناقصا وعن يمينها متزايدا(إشارة المشتقة تتغير من السالب إلى الموجب من اليمين إلى اليسار) 

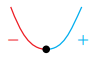
3) نقطة انعطاف أفقي: النقطة الحرجة التي يكون منحنى الاقتران حولها إما متزايدا وإما متناقصا (إشارة المشتقة إما موجبة وإما سالبة).

 

 

تصنيف النقاط الحرجة باستعمال اختبار المشتقة الثانية:

المشتقة الثانية هي الاقتران الذي نحصل عليه من اشتقاق الاقتران مرتين ويسمى باقتران المشتقة الثانية ويرمز له بالرمز f''(x)

يمكننا تحديد النقاط الحرجة في ما إذا كانت عظمة أو صغرى محلية باستعمال المشتقة الثانية بما يسمى اختبار المشتقة الثانية.

1) تكون النقطة الحرجة صغرى محلية إذا كانت المشتقة الثانية عند القيمة الحرجة موجبة (تعويض القيمة الحرجة في المشتقة الثانية يكون موجبا).

2) تكون النقطة الحرجة عظمى محلية إذا كانت المشتقة الثانية عند القيمة الحرجة سالبة (تعويض القيمة الحرجة في المشتقة الثانية يكون سالبا).

 

تمثيل كثيرات الحدود بيانيا:

إيجاد النقاط الحرجة للاقتران وتحديد نوعها يعطي تصورا لشكل منحنى الاقتران لذلك يمكن أن نستعمل النقاط الحرجة في تمثيل كثيرات الحدود بيانيا.