رياضيات فصل أول

الكسور الجزئية

تعلمنا سابقا أن المقدار الجبري النسبي هو كسر بسطه ومقامه كثيرا حدود وأننا نستعمل المضاعف المشترك الأصغر لتوحيد مقامي مقدارين نسبيين مختلفي المقام عند جمعهما أو طرحهما.

سنتعلم اليوم تجزئة المقادير النسبية وهي عبارة عن عملية عكسية للعملية السابقة (عملية توحيد المقام) وينتج عنه كتابة المقدار النسبي على صورة مجموع مقادير نسبية نبسط كلا منها على صورة $\frac{P\left(x\right)}{Q\left(x\right)}$ حيث P و Q كثيرا حدود لا يوجد بينهما عوامل مشتركة ودرجة P أقل من درجة Q وكل من هذه المقادير النسبية يسمى كسرا جزئيا.

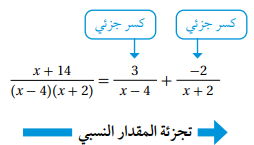
ملاحظة: تعتمد عملية تجزئة المقادير الجبرية النسبية على عوامل المقام.

حالات التجزئة حسب نوع عوامل المقام:

1) عوامل المقام كثيرات حدود خطية مختلفة.

2) عوامل المقام كثيرات حدود خطية أحدها مكرر.

3) عوامل المقام كثيرات حدود أحدها تربيعي غير قابل لتحليل.

سنتعرف على كل حالة على حدى.

تجزئة مقدار نسبي عوامل مقامه كثيرات حدود خطية مختلفة:

في هذه الحالة ينتج كسر جزئي بسطه ثابت ومقامه العامل الخطي على الصورة الآتية.

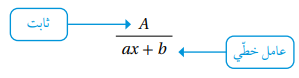
إذا كان Q(x) كثير حدود يمكن تحليله تحليلا كاملا من دون تكرار أي عامل على الصورة الآتية: $Q\left(x\right)=(a_{1}x+b_1)(a_{2}x+b_2)(a_{3}x+b_3)...(a_{n}x+b_n)$ فإنه يمكن تجزئة المقدار الجبري النسبي $\frac{P\left(x\right)}{Q\left(x\right)}$ حيث درجة P أقل من درجة Q، على الصورة الآتية: $\frac{P\left(x\right)}{Q\left(x\right)}=\frac{A_1}{a_{1}x+b_1}+\frac{A_2}{a_{2}x+b_2}+\frac{A_3}{a_{3}x+b_3}+...+\frac{A_n}{a_{n}x+b_n}$

 

تجزئة مقدار نسبي عوامل مقامه كثيرات حدود خطية أحدها مكرر:

إذا كان $\frac{P\left(x\right)}{Q\left(x\right)}$ مقدارا نسبيا وكان التحليل الكامل لQ(x) يحتوي على عامل خطي مكرر n من المرات، ودرجة P أقل من درجة Q؛ فإنه يمكن تجزئة $\frac{P\left(x\right)}{Q\left(x\right)}$ على الصورة الآتية: $\frac{P\left(x\right)}{Q\left(x\right)}=\frac{A_1}{ax+b}+\frac{A_2}{{(ax+b)}^2}+\frac{A_3}{{(ax+b)}^3}+...+\frac{A_n}{{(ax+b)}^n}$

 

تجزئة مقدار نسبي أحد عوامل مقامه كثير حدود تربيعي غير مكرر لا يمكن تحليله:

إذا كان $\frac{P\left(x\right)}{Q\left(x\right)}$ مقدار جبريا نسبيا وكان التحليل الكامل لQ(x) يحتوي على عامل تربيعي غير مكرر لا يمكن تحليله، ودرجة P أقل من درجة Q؛ فإنه يمكن تجزئة $\frac{P\left(x\right)}{Q\left(x\right)}$ على الصورة الآتية: $\frac{P\left(x\right)}{Q\left(x\right)}=\frac{A_{1}x+B_1}{a_1{x}^2+b_{1}x+c_1}+\frac{A_{2}x+B_2}{a_2{x}^2+b_{2}x+c_2}+...+\frac{A_{n}x+B_n}{a_n{x}^2+b_{n}x+c_n}$

 

تجزئة مقدار نسبي درجة كثير الحدود في بسطه مساوية لدرجة كثير الحدود في مقامه أو أكبر منها:

في هذه الحالة نستعمل القسمة الطويلة بقسمة P على Q ثم نكمل تجزئة الكسور.