رياضيات أدبي فصل ثاني

المتتاليات والمتسلسلات

 

فكرة الدرس : تعرُّف المتسلسلة المنتهية ، وإيجاد ، مجموعها.

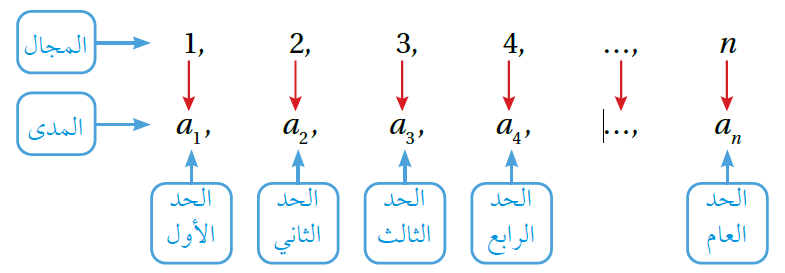
المتتالية : هي مجموعة من الأعداد تتبع ترتيبًا مُعيّنًا ، وأنَّ كل عدد فيها يُسمى حدًا.

تكون المتتالية منتهية إذا حوت عددًا منتهيًا من الحدود ، وتكون غير منتهية إذا حوت  عددًا لا نهائيا من الحدود.

• متتالية منتهية ، مثل : $3 , 7 , 11 , 15$

• متتالية غير منتهية ، مثل : $3 , 7 , 11 , 15 , ...$

تُعدّ المتتالية اقترانًا مجاله مجموعة الأعداد الصحيحة الموجبة، أو مجموعة جزئية منها، ومداه مجموعة جزئية من مجموعة الأعداد الحقيقية ؛ إذ يرتبط كل عدد صحيح في المجال   بعدد حقيقي في المدى ، هو أحد حدود المتتالية.

عند وضع إشارات جمع  (+) بين حدود المتتالية بدلا من الفواصل ، فإنَّها تُسمّى متسلسلة (series).

وكما هو حال المتتالية ، فإنَّ المتسلسلة تكون منتهية إذا حوت عددًا منتهيًا من الحدود، وتكون غير منتهية إذا حوت عددًا لا نهائيا من الحدود.

• متسلسلة منتهية ، مثل : $3 + 6 + 9 +12$

• متسلسلة غير منتهية ، مثل : $3 + 6 + 9 +12 + ...$

---

يُمكِن التعبير عن المتسلسلة بطريقة مختصرة باستعمال رمز المجموع $\left(\sum _{ }\right)$ على النحو الآتي : 

 

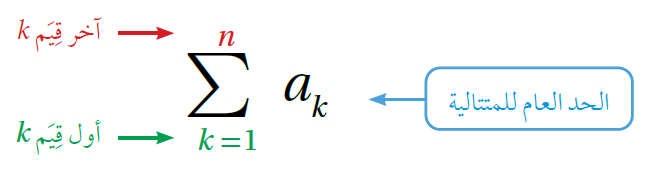
مثال : 

أكتب كل متسلسلة ممّا يأتي باستخدام رمز المجموع :   

$\mathbf{1}\mathbf{)} 4 + 8 + 12 + ... + 32$

الحل : 

أُلاحظ أنّ الحد الأول يساوي ( 1) 4 ،  وأنّ الحد الثاني يساوي ( 2) 4 ، وأنّ الحد الثالث يساوي ( 3) 4، وأنّ الحد الأخير يساوي ( 8) 4.

إذن ، يُمكن كتابة حدود المتتالية على النحو الآتي : 

$a_k = 4k k =1 , 2 , 3 , ... , 8$

بناءً على ذلك، أكتب المتسلسلة باستعمال رمز المجموع كما يأتي :  

                                                                                                                       $\sum _{k=1}^{k=8}\left(4k\right)$

---

 

$\mathbf{2}\mathbf{)} 2 + 5 + 8 + 11 + ...$

الحل : 

أُلاحظ أنّ الحد الأول يساوي  1 - ( 1) 3 ،  وأنّ الحد الثاني يساوي 1 - ( 2) 3 ، وأنّ الحد الثالث يساوي 1 - ( 3) 3    

إذن ، يُمكن كتابة حدود المتتالية على النحو الآتي : 

                                                                                               $\sum _{k=1}^{\infty }(3k - 1)$

---

يُمكن إيجاد مجموع المتسلسلة المنتهية بجمع حدودها. فمثلًا  ، إذا كُتبت المتسلسلة باستخدام رمز المجموع ، فإنَّني أستخدم الحد العام لإيجاد حدودها، ثم جمعها.

مثال : 

أجد مجموع المتسلسلة : $\sum _{k=1}^{k=5}(2k -1)$

الحل : 

اعوض القيم :  $k 1 2 3 4 5 a_k 1 3 5 7 9$     

إذن، مجموع المتسلسلة هو :  

حدود المتسلسلة	$\sum _{k=1}^{k=5}(2k - 1) = 1 + 3 + 5 + 7 + 9$
المجموع	$= 25$

---

إذا كان في المتسلسلة عدد كبير من الحدود، فإنّ إيجاد مجموعها لن يكون سهلًا . ولكنْ توجد قواعد يُمكِن استعمالها لإيجاد مجموع بعض المتسلسلات الخاصة على نحوٍ سهل كما يأتي.

مفهوم أساسي (صيغ لمجموع حالات خاصة من المتسلسلات) 

• مجموع الحد الثابت ( c) إلى نفسه ( n) من المرّات.                                                       $\sum _{k=1}^n c = n \times c$

• مجموع الأعداد الصحيحة المتتالية من (1) إلى (n) .                                               $\underset{k=1}{\overset{n}{\sum }}K = \frac{n(n+1)}{2}$

• مجموع مربعات الأعداد الصحيحة المتتالية من (1) إلى (n) .    $\sum _{k=1}^n K^2 = \frac{n(n+1)(2n+1)}{6}$

 

---