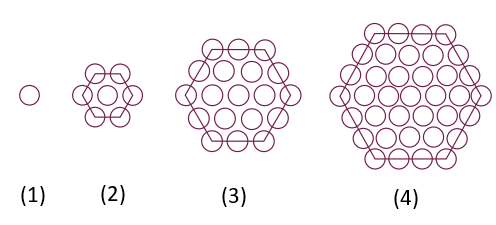رياضيات فصل ثاني

أتحقق من فهمي   صفحة 43

أجد الحدود الثلاثة التالية لكل متتالية مما يأتي :

$a . \frac{5}{2 }, \frac{7}{2} , \frac{9}{2} , \frac{11}{2}, ...$ 

$\frac{13}{2} , \frac{15}{2}, \frac{17}{2}$

b. 5 , 10 , 20 , 40 , ....

80 , 160  , 320

c. 150 , 141 , 132 , 123 , ...

114 , 105 , 96

d. 400 , 200 , 100 , 50 ,...

25 , 12.5 , 6.25

---

أتحقق من فهمي   صفحة 45

أبين إذا كان المقدار الجبري المعطى بجانب كل متتالية  مما يأتي يمثل حدا عاما أم لا ، ثم أصنف المتتاليات إلى خطية ، أو تربيعية ، أو تكعيبية ثم أجد الحد الخامس و السبعين في كل منها :

a) 1 , 3 , 5 , 7 , ... , 2n-1

 

نعم هو الحد العام ، متتالية خطية

T(5 ) = 2(5) - 1 = 10 -1 = 9

T( 70) = 2(70) -1 = 140 -1 = 139

b) 0 ,3, 8, 15 , ... , n² - 1 

نعم هو الحد العام ، متتالية تربيعية 

T(5 ) = 5² -1 = 25 -1 = 24

T(70) = 70² - 1 = 4900 -1 = 4899

c) 1.5 , 8.5 , 27.5 , 27.5 , 64.5 , ... , n³ +0.5

نعم هو الحد العام ، متتالية تكعيبية 

T(5) = 5² + 0.5 = 125.5

T(70) = 70³ +0.5 = 343000 +0.5 = 343000.5

---

أتحقق من فهمي   صفحة 47  (1) 

أجد الحد العام لكل متتالية مما يأتي :

a) 8 , 15 , 22 , 29 , 36 , ...

T(n)= 8+ 7( n -1)

= 8 +7n -7

= 1+ 7n 

b) 4 , 7 , 12 , 19 , 28 , ....

T(n) = n²  +3 

c) -1 , 6 , 25, 62 , 123 , ...

T(n) = n³ - 2 

---

أتحقق من فهمي   صفحة 47      (2)

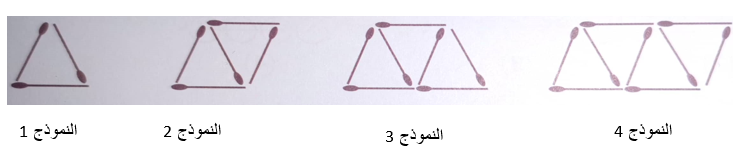
في ما يأتي نمط هندسي يمثل أعواد الثقاب في نماذجه متتالية . أجد الحد العام لهذه المتتالية .

$$\begin{gathered} 1 \to 3 \\ 2 \to 5 \\ 3 \to 7 \\ 4 \to 9 \\ T\left(n\right) = 2n+1 \end{gathered}$$

---

أتدرب و أحل المسائل

أجد الحدود الثلاثة التالية للمتتاليات الآتية :

 1) 6 , 11, 16 , 21 , ...

T(n) = 5n +1

26 , 31 , 36

2) -1 ,6 , 13 , 20 , ...

T(n) = 7n -8

27 , 34 , 41

$3) \frac{3}{2}, \frac{5}{2} , \frac{7}{2} ,\frac{9}{2} , ...$

$T\left(n\right) =\frac{2n +1}{2}$

$\frac{11}{2} , \frac{13}{2} , \frac{15}{2}$

4) -8 , -7 , -6 , -5 , ... 

T(n) = n -9

-4 , -3 , -2 

5) -2 , 1  , 6  ,13 , ...

T(n) = n² -3 

22 , 33 , 46

6) 4 , 16 , 36 , 64 , ...

T(n) = 4n²

100 , 144 , 196

7)3 , 9 , 27 , 81 , ...

T(n) = 3ⁿ

234 , 729 , 2187

8)3 , 8 , 18 , 38 , ...

$T\left(n\right) =\frac{5( 2^n) - 4}{2}$

78 , 158 , 318

9. 128 , 64 , 32 , 16 , ....

$T\left(n\right) = 128 {\left(\frac{1}{2}\right)}^{n -1 }$

8 , 4 , 2 

---

أجد أول خمسة حدود لكل متتالية معطى حدها العام في ما يأتي ، ثم أصنفها إلى متتالية خطية ، أو تربيعية أو تكعيبية 

 10 . n +3

متتالية خطية 

T(1) = 4

T(2) = 5

T(3) = 6

 T(4) =7

T(5) = 8 

11. 3n -1

متتالية خطية

T(1) = 2

T(2) = 5

T(3) = 8

T( 4) = 11

T(5) = 14

12. 4n +5

متتالية خطية

T(1) =9

T(2) =13

T(3) = 17

T(4) = 21

T(5) = 25 

13. n² -1 

متتالية تربيعية 

T( 1) = 0

T(2) = 3

T(3) = 8

T(4) = 15

T(5) = 24

14 . n² +2

متتالية تربيعية

T(1) = 3

T(2) = 6

T(3) = 11

T(4) = 18

T(5) = 27

15. 200 - n²

^{متتالية تربيعية}

^{T(1) = 199}

^{T(2) = 196}

^{T(3) = 191}

^{T(4) = 184}

^{T(5) = 175}

16. n³ +1

متتالية تكعيبية

T(1) = 2

T(2) = 9

T(3) = 28

T(4) = 65

T(5) = 126

17. $\frac{n^2}{2}$ 

متتالية تكعيبية 

$$\begin{gathered} T( 1) =\frac{1}{2} \\ T\left(2\right) =4 \\ T\left(3\right) = \frac{27}{2} \\ T\left(4\right) = 32 \\ T\left(5\right) = \frac{125}{2} \end{gathered}$$

18. 3n³ - 1 

متتالية تكعيبية 

T(1) = 2

T(2) = 23

T(3) = 80

T(4) = 191

T(5) = 374

---

أجد الحد العام لكل متتالية مما يأتي :

19. 21 , 24 , 27 , 30 , 33 , ...

T(n) = 3n +18 

20. 1 , 9 , 17, 25 , 33 , ...

T(n)  = 8n -7 

21. 10 , 13 , 18 , 25 , 34 , ...

T(n) = n² +9 

$22. -\frac{5}{2} , -1 , \frac{3}{2} , 5 , \frac{19}{2 } , ...$

$T\left(n\right) = \frac{n^2 -6 }{2}$

23 . 6 ,13 , 32 , 69 , 130 , ...

T(n) = n³  +5

24. 1 , 15 , 53 , 127 , 249 , ...

T(n) = 2n³ - 1 

---

25. أجد عدد الدوائر في النموذج الخامس من النمط الهندي الآتي :

 

 

$$\begin{gathered} 1 \to 1 \\ 2 \to 7 \\ 3 \to 19 \\ 4 \to 37 \\ T\left(n\right) = 3n^2 - 3n +1 \\ T\left(5\right) = 3\left(25\right) -3\left(5\right) +1 \\ = 75 -15+1 \\ = 61 \end{gathered}$$

---

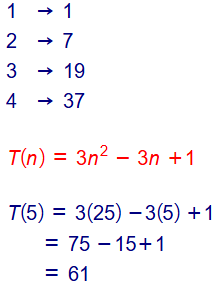
في ما يأتي نمط هندسي يمثل عدد أعواد الثقاب في نماذجه متتالية ، أجد الحد العام لهذه المتتالية :

$$\begin{gathered} 1 \to 4 \\ 2 \to 16 \\ 3 \to 28 \\ T\left(n\right) = 12n -8 \end{gathered}$$

حل آخر:

عند النظر لعدد المربعات 

$$\begin{gathered} 1 \to 2 \\ 2 \to 5 \\ 3 \to 9 \\ T\left(n\right) = 4n -3 \end{gathered}$$

---

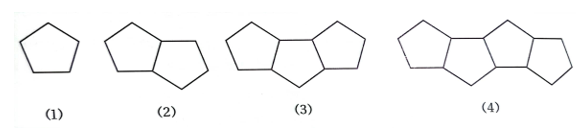
26 . أكمل الجدول الآتي بالاعتماد على نماذج النمط الهندسي أدناه :

النموذج	(1)	(2)	(3)	(4)
المحيط	5	8

27 . أجد محيط نموذج يحتوي n من الأشكال الخماسية .

28. أجد محيط نموذج يحتوي 50 شكلا خماسيًا.

29. ما أكبر عدد من الأشكال الخماسية التي يمكن استعمالها لعمل نموذج محيطه أقل من 1000cm .

T(n) = 3n +2

النموذج	(1)	(2)	(3)	(4)
المحيط	5	8	11	14

T(5) = 3(5) +2 = 15 +2 = 17

T( 50) = 3( 50) +2 = 150+2 = 152

1000 = 3n +2

n = 332

---

مهارات التفكير العليا 

30. تحد : إذا كان الحد العام للمتتالية :  ... 70 , 48 , 30 , 16 , 6  هو :  T(n) = an + bn² ، حيث a , b    عددان حقيقيان ، فأجد قيم a , b .

$$\begin{gathered} 6 = a +b \\ 16 = 2a +4b \to 8 = a +2b \\ 6=a+b-8=a+2b-2=-b \\ b = 2 \\ a =4 \end{gathered}$$

---

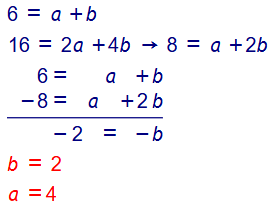
31. تحد :  أجد أول ثلاثة حدود لمتتالية خطية ، إذا كان مجموع هذه الحدود 12 ، وحاصل ضربها 28 .

a + b +c =12

a (b) (c) = 28

a = 1   , b= 4  , c =7

---

32. مسألة مفتوحة : أجد ثلاث متتاليات تبدأ ب 1 ، بحيث يتكون الأولى خطية ، والثانية تربيعية ، والثالثة تكعيبية.

1 , 2 , 3 , 4 , ...

1 , 4 , 9 , 16 , ...

1 , 8 , 27 , 64 , ...

---

كتاب التمارين 

 أكتب الحدود الثلاثة التالية لكل متتالية مما يأتي :

1 )4 , 6 , 8 , 10 , ....

12 , 14 , 16 

2) 3 , 30 , 300 , 3000 , ...

30000 , 300000 , 3000000

3) 1 , 4 , 9 , 16 , ...

25 , 36 , 49

4) 2 , 4 , 8 , 16 ,....

32 , 64 , 128

5) 3 , 10 ,17 ,24 , ...

31 , 38 , 45

6) 0 ,4 , 18 , 48 , ...

100 , 180 , 294

---

أصنف المتتاليات الآتية إلى خطية و تربيعية و تكعيبية و أسية ثم أجد الحدود الثلاثة الأولى و الحد العشرين لكل منها :

7 ) T (n) = 3n +1

متتالية خطية

4 , 7 , 10

8) T(n) = 2n²  +1

متتالية تربيعية

3 , 9 , 19

9) T(n) =5 n³ +2

متتالية تكعيبية 

7 , 42 , 137

10) T(n) = n( n² +1)

متتالية تكعيبية 

2 , 10 , 30

---

أجد الحد العام لكل متتالية مما يأتي :

11) 6 , 11 , 16 , 21 , 26 ,...

T(n) = 6 + 5 ( n -1)

   = 6 +5n -5 

= 5n +1

12 ) -4 , 3 , 22 , 59 , 120 ,...

T(n) = n³ - 5 

13 ) 0 , 3 , 8 , 15 ...

T(n) = n²  -1

14) 5 , 11 , 21 ,35 , 53 ,...

T(n) = 2n² +3

 

---

في ما يأتي نمط هندسي يمثل عدد أعواد الثقاب امتتالية:

15 . أرسم النموذج الرابع في هذا النمط

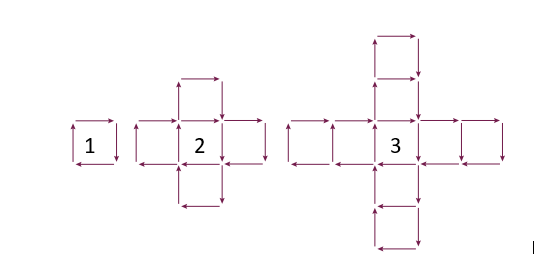
16. أجد عدد أعواد الثقاب اللازمة لبناء النموذج رقم 20 في هذا النمط

T (20) = 9(20) +1

= 181

18  . ما أكبر مجموعة من االنماذج التي  يمكن بناؤها باستعمال 100 عود من الثقاب ؟  

$$\begin{gathered} 100 = 9n +1 \\ 99 = 9n \\ n = 11 \end{gathered}$$