الفيزياء 11 فصل ثاني

الشحنات الكهربائية تؤثر بقوة في شحنة نقطية صغيرة تُسمَّى شحنة اختبار  (q)، موضوعة بالقرب منها حسب قانون كولوم، وأن كلًّا من مقدار هذه القوة واتّجاهها يتغيّر بتغيّر موضع شحنة الاختبار بالنسبة للشحنة. إنّ الشحنات الكهربائيّة تولّد في الحيّز المحيط بها خاصيّة تظهر على شكل قوى كهربائية تُسمَّى المجال الكهربائي، وعند وضع شحنة أخرى في هذا الحيز؛ فإنّها تتأثر بهذا المجال على نحو ينسجم مع قانون كولوم. وتُعرف شدة المجال الكهربائي (E) عند نقطةٍ ما بأنّها القوة التي يؤثّر بها المجال على وحدة الشحنات الموجبة الموضوعة فى تلك النقطة. فإذا كانت قيمة شحنة الاختبار الموضوعة فى نقطة معينة فى المجال هى (q).

فتكـون شـدة المجـال:

$E⃗=\frac{F⃗}{q_0}$

 

نلاحظ أنّ شدة المجال مرتبطة بالقوة فهي لذلك كمية متّجهة، ويكون اتّجاهها في نقطة ما باتّجاه القوة المؤثّرة في شحنة الاختبار الموجبة الموضوعة في تلك النقطة. وبالرجوع إلى المعادلة أعلاه فإنّ وحدة شدة المجال الكهربائي E هي N/C.

إنّ هذه العلاقة تمكنّنا من معرفة شدة المجال الكهربائي دون معرفة الشحنة أو الشحنات المولّدة له. فإذا كان المجال ناتجاً عن شحنة نقطية (q)، فإنّ مقدار القوة الكهربائية المتبادلة بين الشحنتين ($q,q_0$) يكون:

$\mathit{F}\mathbf{=}\mathit{k}\frac{\mathbf{q}{\mathbf{q}}_{\mathbf{0}}}{{\mathbf{r}}^{\mathbf{2}}}\mathbf{\to }\mathit{E}\mathbf{=}\frac{\mathbf{F}}{{\mathbf{q}}_{\mathbf{0}}}\mathbf{=}\frac{\mathbf{k}{\displaystyle \frac{\mathbf{q}{\mathbf{q}}_{\mathbf{0}}}{{\mathbf{r}}^{\mathbf{2}}}}}{{\mathbf{q}}_{\mathbf{0}}}\mathbf{=}\mathit{k}\frac{\mathbf{q}}{{\mathbf{r}}^{\mathbf{2}}}\mathbf{=}\mathbf{9}\mathbf{\times }{\mathbf{10}}^{\mathbf{9}}\mathbf{\times }\frac{\mathbf{q}}{{\mathbf{r}}^{\mathbf{2}}}$

 

حيث  

 

 

 

r: بُعد النقطة المطلوب حساب شدة المجال عندها عن الشحنة (

q).

ويكون اتّجاه المجال باتّجاه القوة المؤثّرة في شحنة الاختبار الموجبة (${\mathit{q}}_{\mathbf{0}}$)؛ أي مبتعداً عن الشحنة الموجبة، ومقترباً من الشحنة السالبة. ولحساب شدة المجال الكهربائي الناشئ عن عدد من الشحنات الكهربائيّة عند نقطة في مجالها المشترك نفترض أولاً وجود وحدة الشحنات الموجبة عند هذه النقطة، ثم نحسب شدة المجال الكهربائي عند النقطة لكلّ شحنة، فتكون شدة المجال الكلي الناتج تساوي محصّلة مجالات الشحنات عند تلك النقطة؛ لأنّ المجال الكهربائى كمية متجهة؛ أي أنّ:

$\overrightarrow{E_1}=\overrightarrow{E_{21}}+\overrightarrow{E_{31}}+\overrightarrow{E_{41}}+\cdots$

---

المثال (5): شحنة كهربائيّة نقطية موجبة موضوعة في الهواء مقدارها ($\mathbf{5}\mathit{\mu }\mathit{c}$).أُحدّد اتّجاه المجال عند النقاط (a,b,c)، ثمّ أجد مقدار المجال الكهربائيّ عند النقطة (a) التي تبعد عن الشحنة مسافة $\mathbf{36}\mathit{c}\mathit{m}$ والمبيّنة في الشكل التالي.

 

الحل:

لتحديد اتّجاه المجال عند كل نقطة من (a, b ,c) أفترض وجود شحنة اختبار موجبة عند كُلِّ منها، وأحدّد اتجاه لقوّة المؤثّرة في كلّ شحنة اختبار، ويكون اتجاه المجال في اتجاه القوّة نفسه.

وبذلك فإن اتّجاه المجال عند (a) يكون باتجاه محور (x( *)*)، وعند النقطة (b) يكون باتّجاه محور    (x-)، وعند النقطة(c)، يكون باتّجاه محور (y( *)*)، كما في الشكل (16/ ب).

ولمعرفة مقدار المجال؛ أستعملُ العلاقة الآتية:

$\mathit{E}\mathbf{=}\mathit{k}\frac{\mathbf{q}}{{\mathbf{r}}^{\mathbf{2}}}\mathbf{=}\mathbf{9}\mathbf{\times }{\mathbf{10}}^{\mathbf{9}}\mathbf{\times }\frac{\mathbf{5}\mathbf{\times }{\mathbf{10}}^{\mathbf{-}\mathbf{6}}}{\mathbf{(}\mathbf{36}{\mathbf{)}}^{\mathbf{2}}\mathbf{\times }{\mathbf{10}}^{\mathbf{-}\mathbf{4}}}$

${\mathit{E}}_{\mathbf{a}}\mathbf{=}\mathbf{3}\mathbf{.}\mathbf{47}\mathbf{\times }{\mathbf{10}}^{\mathbf{5}}\mathit{N}\mathbf{/}\mathit{C}$

 

---

تمرين : في المثال السابق؛ أجد مقدار القوّة الكهربائيّة التي يؤثّر بها المجال الكهربائيّ في شحنة مقدارها ($\mathbf{-}\mathbf{3}\mathit{n}\mathit{C}$) موضوعة عند النقطة (a)، ثمّ أُحدّد اتّجاه هذه القوّة.

الحل:

$\mathit{E}\mathbf{=}\frac{\mathbf{F}}{{\mathbf{q}}_{\mathbf{0}}}\mathbf{\to }\mathbf{3}\mathbf{.}\mathbf{47}\mathbf{\times }{\mathbf{10}}^{\mathbf{5}}\frac{\mathbf{N}}{\mathbf{C}}\mathbf{=}\frac{\mathbf{F}}{\mathbf{3}\mathbf{\times }{\mathbf{10}}^{\mathbf{-}\mathbf{9}}}\mathbf{\Rightarrow }\mathit{F}\mathbf{=}\mathbf{10}\mathbf{.}\mathbf{41}\mathbf{\times }{\mathbf{10}}^{\mathbf{-}\mathbf{4}}\mathbf{ }\mathit{N}$

 

يكون إتجاه الشحنة الموضوعة عند النقطة (a) نحو (-x) لأنها شحنة سالبة فتتولد قوة تجاذب بينهما.

---

عند وضع عدد من الشحنات الكهربائيّة المتشابهة أو المختلفة في منطقة واحدة بتوزيع معيّن، تنشأ حول كلّ منها منطقة مجال كهربائيّ، بحيث يكون المجال الكهربائيّ المحصّل عند أيّ نقطة في هذه المنطقة مساويًا لمحصّلة المجالات الناتجة عن كل شحنة إذا كانت منفردة، كما يتضح في الأمثلة الآتية. وستقتصر دراستنا للشحنات المُوزَّعة في مستوى ثنائي الأبعاد فقط.

 

المثال (6) : يوضّح الشكل شحنتين موجبتين نقطيتين (Q₂,Q₁)، موضوعتين في الهواء وتفصلهما مسافة $(40 cm)$ . أحسب المجال الكهربائي المحصل عند نقطة (a) تقع على الخط الواصل بينهما وتبعد عن الشحنة $\left(Q_2\right)$ مسافة  $(10 cm)$، وأحدّد اتجاه المجال.

الحل:

$r_1 = r - r_2 = 40 - 10 = 30 cm$

مقدار المجال الناتج عن الشحنة ( Q₁ ) عند النقطة (a):

$E_1=k\frac{Q_1}{{r^2}_1}=9\times {10}^9\times \frac{6\times {10}^{-6}}{(30\times {10}^{-2}{)}^2}$

  $E_1=6\times {10}^5 N/C$  باتجاه محور $-x$

ومقدار المجال الناتج عن الشحنة ( Q₂ ) عند النقطة :   

$E_2=k\frac{Q_2}{{r^2}_2}=9\times {10}^9\times \frac{2\times {10}^{-6}}{(10\times {10}^{-2}{)}^2}$

$E_2=18\times {10}^{5}N/C$ باتجاه محور $+x$

$E=E_2-E_1=18\times {10}^5-6\times {10}^5=12\times {10}^{5}N/C$

اتجاه المجال الكهربائي باتجاه محور(+X)

---

المثال (7) يوضّح الشكل شحنتين نقطيتين في الهواء، الأولى سالبة والثانية موجبة. أستعين بالشكل؛ وأجد المجال الكهربائيّ المحصّل عند النقطة ( a) وأُحدّد اتّجاهه.

$E_1=k\frac{Q_1}{{r^2}_1}=9\times {10}^9\times \frac{3\times {10}^{-6}}{(6\times {10}^{-2}{)}^2}$

$E_1=7.5\times {10}^{6}N/C$  باتجاه محور +Y

$E_2=k\frac{Q_2}{{r^2}_2}=9\times {10}^9\times \frac{4\times {10}^{-6}}{(15\times {10}^{-2}{)}^2}$

$E_2=1.6\times {10}^{6}N/C$ باتجاه محور +x

اتّجاه المجال الناتج عن الشحنة الثانية يكون باتّجاه محور (x+) أُلاحظ أنّ الزاوية بين متّجهي المجالين (°90)، كما في الشكل ، فيحسب المجال المحصل باستعمال العلاقة:

$E=\sqrt{(E_1{)}^2+(E_2{)}^2}$

$E=\sqrt{(7.5\times {10}^6{)}^2+(1.6\times {10}^6{)}^2}$

$E=\sqrt{56.25\times {10}^{12}+2.56\times {10}^{12}}$

$E=7.67\times {10}^6 N/C$

ويُحدّد اتّجاه المجال المحصّل بالزاوية المرجعية ) θ(حيث:

$tan\theta =\frac{7.5\times {10}^6}{1.6\times {10}^6}=4.69$

$\theta ={\tan }^{-1 }4.88=78°$

$E=7.67\times {10}^6 N/C , 78°$

---

تمرين : يوضّح الشكل شحنتين نقطيتين في الهواء: الأولى موجبة والثانية سالبة، تفصلهما مسافة (1.8m). أستعين بالشكل؛ وأجد المجال الكهربائيّ المحصّل عند نقطة تنصّف المسافة بين الشحنتين.

$E_1=k\frac{Q_1}{{r^2}_1}=9\times {10}^9\times \frac{(3\times {10}^{-6})}{(9\times {10}^{-1}{)}^2}$

$E_1=9\times {10}^9\times \frac{3\times {10}^{-6}}{81\times {10}^{-2}}$

$E_1=3.34\times {10}^4 N/C$  باتجاه محور $-x$

 $E_2=k\frac{Q_2}{{r^2}_2}=9\times {10}^9\times \frac{1\times {10}^{-6}}{(9\times {10}^{-1}{)}^2}$

$E_2=1.11\times {10}^4 N/C$  باتجاه محور $+\mathrm{x}$

$E=E_2+E_1=1.11\times {10}^4+3.34\times {10}^4=4.45\times {10}^{4}N/C$

اتجاه المجال الكهربائي باتجاه محور $(-x)$ 
 

---

مثال ( 8) ثلاث شحنات كهربائية، موزَّعة في الهواء، مقاديرها كما هو مثبت في الشكل. أحسب مقدار المجال الكهربائي المحصل عند النقطة ( a) وأحدّد اتجاهه.

الحل:

$E_1=k\frac{Q_1}{{r^2}_1}=9\times {10}^9\times \frac{(6.4\times {10}^{-6})}{(0.5{)}^2} E_1= 2.3\times {10}^5 N/C$

$E_2=k\frac{Q_2}{{r^2}_2}=9\times {10}^9\times \frac{(3.6\times {10}^{-6})}{(0.4{)}^2} E_2=2\times {10}^5 N/C$

$E_3=k\frac{Q_3}{{r^2}_3}=9\times {10}^9\times \frac{27\times {10}^{-6}}{(0.9{)}^2 } E_3=3\times {10}^{5}N/C$

بمراعاة أنواع الشحنات ومواقعها نجد أن اتجاهات المجالات الكهربائية الثلاث تكون كما في الشكل أ، ثم نحلّل كل مجال إلى مركّبتين؛ على محور ( x) وعلى محور ( y)، كما في الشكل ب.

تحليل كل مجال إلى مركّبتين:

المحصلة الأفقية للمجال:

$Ex=E1x-E3x=1.38\times {10}^5-2.61\times {10}^5=-1.23\times {10}^5 N/C$

المحصلة العمودية للمجال:

$Ey=E1y-E2y+E3y=1.84\times {10}^5-2.0\times 105+1.5\times {10}^5=1.34\times {10}^5 N/C$

مقدار المجال المحصل عند النقطة ( a) يساوي:

$E=\sqrt{(E_X{)}^2+(E_Y{)}^2}=\sqrt{(1.23\times {10}^5{)}^2+(1.34\times {10}^5{)}^2}=\sqrt{3.31\times {10}^{10}}=1.82\times {10}^5 N/C$

 

اتجاه المجال المحصل عند النقطة ( a) يصنع مع محور (-X) زاوية مقدارها ∅ حيث :

$tan\varnothing =\frac{E_y}{E_x}=\frac{1.34\times {10}^5}{-1.23\times {10}^5}=-1.09$

$\varnothing =47.5°$

---

يمكن تمثيل المجال الكهربائي بخطوط تُسمّى خطوط المجال الكهربائي، وتدل على المسار الذي تسلكه شحنة الاختبار الموجبة عند تحركها في المجال بتأثير قوة المجال،

ولخطوط المجال الكهربائي الخصائص الآتية:

1. يدل اتّجاه المماس لخط المجال الكهربائي عند أيّة نقطة على اتّجاه المجال الكهربائي عند تلك النقطة،
2. وتكون خارجة من الشحنة الموجبة وداخلة إلى السالبة، ويتناسب عددها مع مقدار الشحنة.
3. تتناسب كثافة خطوط المجال الكهربائي طرديّاً مع شدة المجال الكهربائي (كثافة الخطوط: عدد خطوط المجال الكهربائي التي يقطع وحدة المساحة العمودية على اتّجاهها).

ويبيّن الشكل خطوط المجال الكهربائى لبعض الشحنات الكهربائيّة.

 

المثال (9) :يبيّن الشكل خطوط المجال الكهربائي الناشئ عن شحنتين نقطيتين متجاورتين موضوعتين في الهواء. اعتمادًا على الشكل، وإذا علمت أن الرموز  $({\mathrm{A}}_1, {\mathrm{A}}_2, {\mathrm{A}}_3, {\mathrm{A}}_4)$ تدل على أربع مناطق متساوية في المساحة تقع ضمن المجال، فأجيب عن السؤالين الآتيين:

أ . أرتّب المناطق الأربعة $( {\mathrm{A}}_1-{\mathrm{A}}_4)$ تصاعديًّا حسب مقدار المجال في كل منطقة. أوضّح السبب.

ب. أحدد نوع كل شحنة، وأحدد أي الشحنتين أكبر مقدارًا. أفسر إجابتي.

الحل:

أ . حسب خصائص خطوط المجال الكهربائي ، فإن مقدار المجال يزداد حيثما تتزاحم خطوطه، فالمنطقة (A1)يخترقها خط واحد، ثم المنطقة ( A4 ) يخترقها خطان، ثم المنطقة ( A2 ) يخترقها ثلاثة خطوط. فيكون الترتيب التصاعدي $({\mathrm{A}}_1 < {\mathrm{A}}_4 < {\mathrm{A}}_2 < {\mathrm{A}}_3)$

ب. الشحنة ( Q2 ) سالبة، وأكبر مقدارًا من الشحنة الموجبة ( Q1 )؛ لأن عدد خطوط المجال التي تدخل في الشحنة ( Q2 ) أكثر من تلك التي تخرج من الشحنة ( Q1 )، كما أن الخطوط أكثر تزاحمًا بالقرب من (Q2).

---

المثال (10): النقطة ( a) والشحنتان المتساويتان في المقدار ( Q1 ) سالبة و  (Q2) موجبة، تشكّل معًا في الهواء مثلثًا متساوي الأضلاع طول ضلعه ( d) ، كما في الشكل) أ(. إذا كانت النقطة ( b) تنصّف المسافة بين الشحنتين، فأجد نسبة مقدار المجال عند ( b) إلى مقداره عند (a) .

الحل:

أولاً: المجال الكهربائي عند النقطة ( b) التي تبعد عن كل $E_{a1}=E_{a2}=k\frac{Q}{(d{)}^2}$شحنة مسافة $\frac{d}{2}$

الشحنتان المولدتان للمجال متساويتان$Q_1= Q_2=Q$ ، وبعد النقطة عن كل منهما $\frac{d}{2}$ ،فيكون المجالان الناشئان عنهما متساويين، ومقدار كل منهما:

$E=k\frac{Q}{r^2}$

$E_{b1}=E_{b2}=k\frac{Q}{(\frac{d}{2}{)}^2}=4k\frac{Q}{d^2}$

وبما أن المجالين بالاتجاه نفسه، فإن المجال المحصل:

$E_b=E_{b1}+E_{b2}=4k\frac{Q}{d^2}+4k\frac{Q}{d^2}=8k\frac{Q}{d^2}$

ثانيًا: المجال الكهربائي عند النقطة ( a) التي تبعد عن كل شحنة مسافة (d) :

المجالان الناشئان عن الشحنتين متساويان ومقدار كل منهما:

$E_{a1}=E_{a2}=k\frac{Q}{(d{)}^2}$

لإيجاد المجال المحصل، نحدد اتجاهي المجالين ونحلل كلًّ منهما إلى مركبتيه ، كما يبين الشكل المركبتان ( E1y ) و ( E2y ) متساويتان ومتعاكستان، أي أن:

$Ey = E2y - E1y = 0$

 

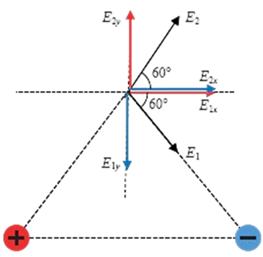
المركبتان ( E1x ) و ( E2x ) متساويتان في المقدار، ومقدار كل منهما:

$E_{1x}=E_{2x}=k\frac{Q}{(d{)}^2}cos60°=\frac{1}{2}k\frac{Q}{d^2}$

فيكون المجال المحصل عند النقطة (a):

$E_a=E_{1x}+E_{2x}=\frac{1}{2}k\frac{Q}{d^2}+\frac{1}{2}k\frac{Q}{d^2}=k\frac{Q}{d^2}$

نسبة $E_b$ إلى $E_a$

$E_b=8E_a\to \frac{E_b}{E_a}=8$