رياضيات فصل أول

المسافة في المُستوى الإحداثيّ

أولًا  : المسافة بين نقطتين

المسافةُ بينَ نقطتَيْنِ على خطِّ الأعدادِ هِيَ طولُ القطعةِ المستقيمةِ الواصلةِ بين هاتين النقطتين بحيث تُمثّلان نهايتيِ القطعة ، ويمكن

استعمال إحداثِيّ كلّ من النقطتين لإيجاد المسافةِ بينَهُما.

•• مفهومٌ أساسيٌّ (صيغةُ المسافةِ على خطِّ الأعدادِ)

بالكلماتِ : المسافة بين نقطتَيْن على خطِّ الأعدادِ هِيَ القيمةُ المُطلقةُ للفرقِ بين إحداثِيَّيْهِما. بالرُّموز : إذا كانَ إحداثيُّ النقطة A على خطِّ  الأعداد هو x1 وإحداثيُّ النقطة B هو x2  ، فإنَّ $AB = |x_2 - x_1| or AB = |x_1 - x_2|$

 

 

 

 

 

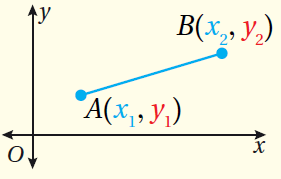
•• مفهوم أساسي (صيغةُ المسافةِ في المُستوى الإحداثِيِّ)

المسافةُ بينَ النقطتَيْنِ ( A(x1 , y1 وَ ( B(x2 , y2 ، هِيَ : $AB = \sqrt{{(x_2 - x_1)}^2 + {(y_2 - y_1)}^2}$

 

 

 

 

 

ثانيًا : نقطةُ مُنتصفِ القطعةِ المستقيمةِ

نقطةُ مُنتصفِ القطعةِ المستقيمةِ هِيَ النقطةُ التي تقعُ في مُنتصفِ المسافةِ بينَ نقطتَيْ نهايَتَيِ القطعةِ المستقيمةِ.

 

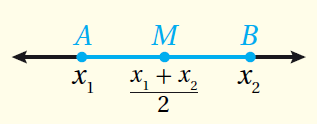
•• مفهومٌ أساسيٌّ (صيغةُ نقطةِ المُنتصفِ على خطِّ الأعدادِ)

إذا كانَ إحداثِيُّ النقطةِ A على خطِّ الأعدادِ هُوَ x1  وَإحداثِيُّ النقطةِ B هُوَ x2 ، وكانتْ M نقطةَ مُنتصفِ AB ، فإنَّ  إحداثِيَّ M هُوَ :                      $\frac{x_1 + x_2}{2}$

 

 

 

 

 

 

 

•• مفهومٌ أساسيٌّ (صيغةُ نقطةِ المُنتصفِ في المُستوى الإحداثِيِّ)

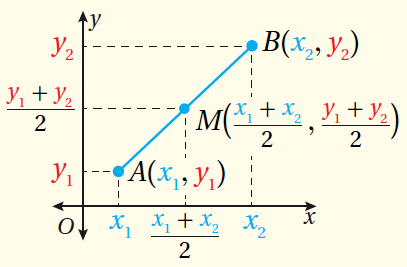إذا كانت $B(x_2 , y_2) و A(x_1 , y_1)$   نقطتَيْنِ في المُستوى الإحداثِيِّ ، وَ M نقطةَ مُنتصفِ AB ، فإنَّ إحداثِيَّيْ M  هُما :       $M (\frac{x_1 + x_2}{2} , \frac{y_1 + y_2}{2})$