رياضيات7 فصل أول

حلول أسئلة أتحقق من فهمي 

4) أيُّ القطعِ المستقيمةِ توازي $\overline{\mathbf{EH}}$

$\overline{\mathrm{FG}}, \overline{\mathrm{AD}} , \overline{\mathrm{BC}}$

5) أُسمّي مستوًى موازيًا للمستوى ABFE 

المستوى DCGH

6)  أُسمّي قطعتيْنِ مستقيمتيْنِ موازيتيْنِ للمستوى EFGH

$\overline{\mathrm{AB}} , \overline{\mathrm{BC}}$

 

اختيارٌ منْ مُتعدِّدٍ: في الشكلِ أعلاهُ، أيُّ أزواجِ الزوايا الآتيةِ مُتبادَلتانِ داخليًّا؟ 

$\mathbf{\text{a) ∠1, ∠6 b) ∠3, ∠7}}\mathbf{ }\mathbf{\text{c) ∠3, ∠5}}\mathbf{ }\mathbf{\text{d) ∠1, ∠7}}$

الزاويتان 1 و 7 ، زاويتان غير متجاورتين تقعان في المنطقة تقعانِ في المنطقةِ الداخليةِ، وفي جهتيْنِ مختلفتيْنِ منَ القاطعِ.

الإجابة الصحيحة d

 

4) $\mathbf{m}\mathbf{\angle }\mathbf{1}$

$$\begin{gathered} \mathrm{m}\angle 1=\mathrm{m}\angle 3 \\ \mathrm{m}\angle 1=70° \end{gathered}$$                                             زاويتان متقابلتان بالرأس

5) $\mathbf{m}\mathbf{\angle }\mathbf{4}$

$$\begin{gathered} \mathrm{m}\angle 4=\mathrm{m}\angle 1 \\ \mathrm{m}\angle 4=70° \end{gathered}$$                                             زاويتان متناظرتان

6) $\mathbf{m}\mathbf{\angle }\mathbf{6}$

$\mathrm{m}\angle 6=110°$                                             زاويتان متبادلتان خارجيا

7) $\mathbf{m}\mathbf{\angle }\mathbf{7}$

$$\begin{gathered} \mathrm{m}\angle 7=\mathrm{m}\angle 1 \\ \mathrm{m}\angle 7=70° \end{gathered}$$                                             زاويتان متبادلتان خارجيا

---

---

حلول أسئلة أتدرب وأحل المسائل 

أستعينُ بالمنشورِ الخماسيِ المجاورِ للإجابةِ عنِ الأسئلةِ الآتيةِ:

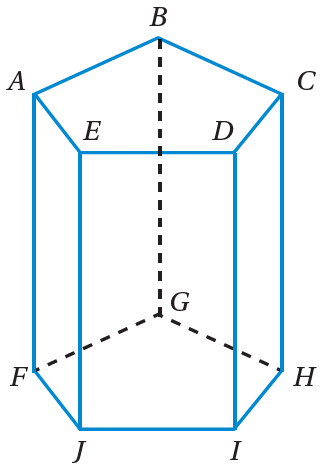
1) أيُّ القطعِ المستقيمةِ توازي $\overline{\mathbf{AB}}$

$\overline{\mathrm{FG}}$

2) أُسمّي مستوييْنِ متوازييْنِ.

$\mathrm{ABCDE} , \mathrm{FGHIJ}$

3) أُسمّي قطعتيْنِ مستقيمتيْنِ موازيتيْنِ للمستوى AEJF

$\overline{\mathrm{DI}} ,\overline{\mathrm{BG}}$

 

اعتمادًا على الشكلِ المجاورِ، أُسَمّي: 

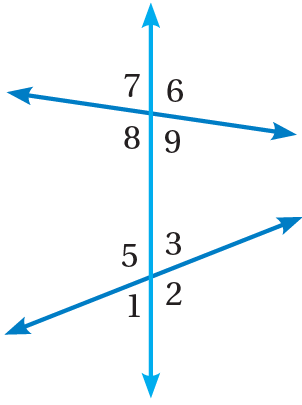
4) زاويتينِ متناظرتينِ.

$\angle 6,\angle 3$

5) زاويتينِ متبادلتينِ داخليًّا.

$\angle 9,\angle 5 \mathrm{أو} \angle 8,\angle 3$

6) زاويتينِ متبادلتينِ خارجيًّا.

$\angle 6,\angle 1 \mathrm{أو} \angle 7,\angle 2$

7) زاويتينِ داخِليَّتينِ في جهَةٍ واحدةٍ.

$\angle 8,\angle 5 \mathrm{أو} \angle 9,\angle 3$

 

مستشفياتٌ: في الشكلِ المجاورِ سريرٌ طبِّيٌّ ذو سِياجٍ لحمايةِ المريضِ منْ خطرِ السقوطِ. إذا كانَ هذا السياجُ مُوازِيًا لِسَطحِ السريرِ، والدّعاماتُ موازِيةً بعضَها، فأجدُ ما يأتي:

8) $\mathbf{m}\mathbf{\angle }\mathbf{1}$

$\mathrm{m}\angle 1=98°$                                                  زاويتان متناظرتان

9) $\mathbf{m}\mathbf{\angle }\mathbf{2}$

$$\begin{gathered} \mathrm{m}\angle 2+\mathrm{m}\angle 1=180° \\ \mathrm{m}\angle 2=82° \end{gathered}$$                                   زاويتان داخليتان من جهة واحدة

10) $\mathbf{m}\mathbf{\angle }\mathbf{3}$

$\mathrm{m}\angle 3=98°$                                                  زاويتان متبادلتان داخليا

11) $\mathbf{m}\mathbf{\angle }\mathbf{4}$

$$\begin{gathered} \mathrm{m}\angle 4=180°-98° \\ \mathrm{m}\angle 4=82° \end{gathered}$$

 

في الشكلِ المجاورِ، أجدُ قياسَ كلٍّ منَ الزوايا الآتيةِ: 

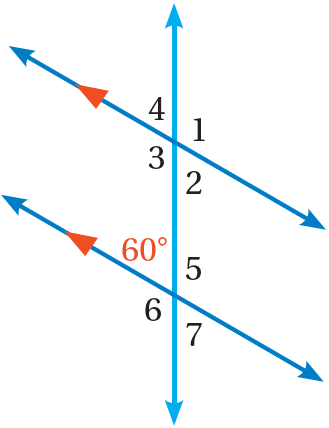
12) $\mathbf{m}\mathbf{\angle }\mathbf{3}$

$$\begin{gathered} \mathrm{m}\angle 3+60°=180° \\ \mathrm{m}\angle 3=120° \end{gathered}$$                                     زاويتان داخليتان من جهة واحدة

13) $\mathbf{m}\mathbf{\angle }\mathbf{5}$

$$\begin{gathered} \mathrm{m}\angle 5=\mathrm{m}\angle 3 \\ \mathrm{m}\angle 5=120° \end{gathered}$$                                              زاويتان متبادلتان داخليا

14) $\mathbf{m}\mathbf{\angle }\mathbf{4}$

$\mathrm{m}\angle 4=60°$                                                 زاويتان متناظرتان

15) $\mathbf{m}\mathbf{\angle }\mathbf{2}$

$\mathrm{m}\angle 2=60°$                                                 زاويتان متبادلتان داخليا

16) $\mathbf{m}\mathbf{\angle }\mathbf{1}$

$$\begin{gathered} \mathrm{m}\angle 1=\mathrm{m}\angle 5 \\ \mathrm{m}\angle 1=120° \end{gathered}$$                                               زاويتان متناظرتان

17) $\mathbf{m}\mathbf{\angle }\mathbf{6}$

$$\begin{gathered} \mathrm{m}\angle 6=\mathrm{m}\angle 3 \\ \mathrm{m}\angle 6=120° \end{gathered}$$                                               زاويتان متناظرتان

 

18) جَبْرٌ: معتمدًا الشكلَ المجاورَ، أكتبُ معادلةً ثمَّ أحلُّها لأجدَ قيمةَ x

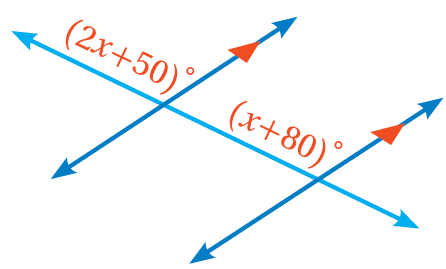
الزوايتان متناظرتان

$$\begin{gathered} (2\mathrm{x}+50)°= (\mathrm{x}+80)° \\ \mathrm{x}=30° \end{gathered}$$

 

19) أجدُ قيمةَ x في الشكلِ المجاورِ. 

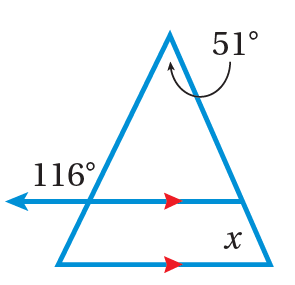
نجد مجموع قياسات المثلث الصغير

$180°-116=64°$                                       قياس الزاوية المكملة للزاوية الخارجية 116

$180°-\left(62°+51°\right)=65°$                           مجموع قياس المثلث الصغير

نجد قياس الزاوية x

$\angle \mathrm{x}=65°$                                                   زاويتان متناظرتان  

 

تبريرٌ: معتمدًا الشكلَ المجاورَ، أي العباراتِ الآتيةِ صحيحةٌ، وأيُّها خطأٌ، مُبرِّرًا إجابتي: 

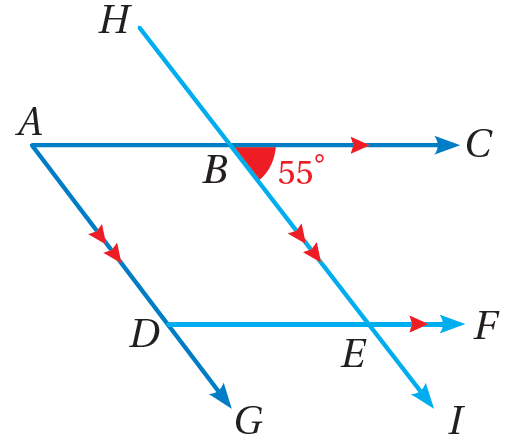
20) $\mathbf{\angle }\mathbf{CAG}\mathbf{،}\mathbf{\angle }\mathbf{FDG}$ متناظرتانِ. 

صحيحة ، تقعان في جهة واحدة من القاطع احدهما داخلية والاخرى خارجية

21) $\mathbf{m}\mathbf{\angle }\mathbf{HBC}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{m}\mathbf{\angle }\mathbf{BED}$

خطا، لا توجد علاقة بينهما لذلك قياس الزوايا غير متساوي

22) $\mathbf{\angle }\mathbf{BED}\mathbf{ }\mathbf{،}\mathbf{\angle }\mathbf{EDG}$

صحيحة ، غير متجاورتين و داخليتان وفي جهتين مختلفتين من القاطع.

23) $\mathbf{m}\mathbf{\angle }\mathbf{BED}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{55}\mathbf{°}$

صحيحة ، متبادلة داخليا مع ∠CBE

24)  $\mathbf{\angle }\mathbf{ABE}\mathbf{ }\mathbf{،}\mathbf{\angle }\mathbf{ADF}$ متناظرتانِ

خطأ ، الزاويتان لا يوجد علاقة بينهما

 

25) تبريرٌ: متى تتساوى جميعُ قياساتِ الزوايا الناتجةِ منْ تقاطعِ مستقيمٍ معَ مستقيمينِ متوزايينِ؟ أبرِّرُ إجابتي.

عندما يعامد القاطع كلا المســتقيمين المتوازيين. في هذه الحالة تكون كل الزوايا قائمة.

 

26) أكتب : كيفَ أجدُ قياسَ جميعِ الزوايا الثمانيةِ الناتجةِ منْ تقاطعِ مستقيمٍ معَ مستقيمينِ متوازيينِ إذا علمْتُ قياسَ واحدةٍ منْها؟

من خلال العلاقات بين الزوايا (التناظر ، التبادل ، الزوايا الداخلية من جهة واحدة)

---

---

حلول أسئلة كتاب التمارين 

أُحدِّدُ ما إِذا كانَت كُلُّ زاويتَينِ في ما يأتي متبادِلتيْنِ داخليًّا أو مُتَناظِرتَينِ: 

1)

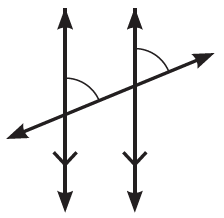
متناظرتين

2)

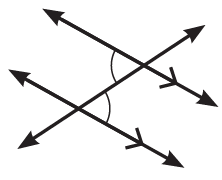
متبادِلتيْنِ داخليًّا

3)

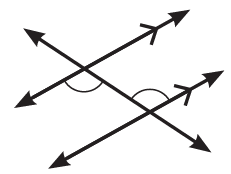
متبادِلتيْنِ داخليًّا

4) 

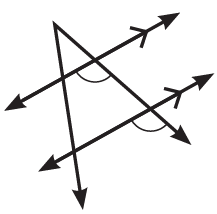
متناظرتين

 

5) أُحدِّدُ جميعَ الزّوايا الّتي قِياسُها يُساوي $\mathbf{60}\mathbf{°}$ في الشّكْلِ المُجاوِرِ. أبَرِّرُ إجابتِي

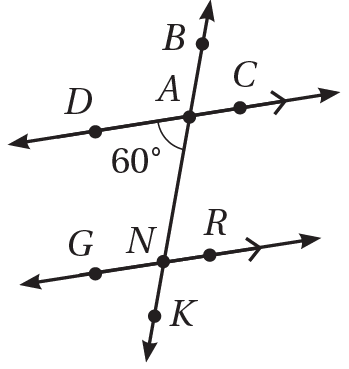
$\angle \mathrm{KNG}$                                                              بالتناظر

$\angle \mathrm{ANR}$                                                             متبادلة داخلية

$\angle \mathrm{BAC}$                                                              متقابلة بالرأس مع $\angle \mathrm{DAN}$

 

أجدُ قِياساتِ الزّوايا المجهولةَ في كُلٍّ شكلٍ مِمّا يأْتي، مُبَرّرًا إجابَتي:

6)

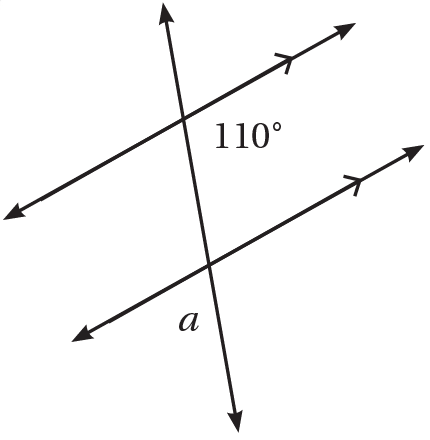
نجد قياس الزاوية المكملة لل110

$180°-110°=70°$

نجد قياس الزاوية a بالتناظر

$\mathrm{m}\angle \mathrm{a}=70°$

 

7)

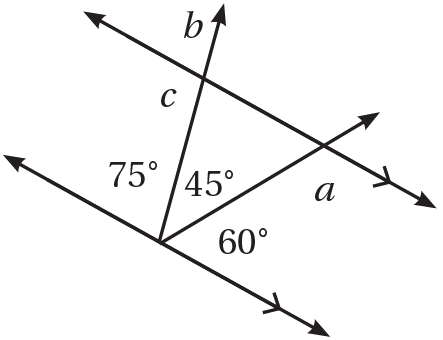
$\mathbf{m}\mathbf{\angle }\mathbf{a}\mathbf{=}120°$                                                   متحالفة مع زاوية قياسها °60، والتحالف ناتج عن قاطع لمتوازيين

$\mathbf{m}\mathbf{\angle }\mathbf{b}\mathbf{=}75°$                                                     متناظرة مع زاوية قياسها °75

$\mathbf{m}\mathbf{\angle }\mathbf{c}\mathbf{=}105°$                                                   متحالفة مع زاوية قياسها °75 ، والتحالف ناتج عن قاطع لمتوازيين.

8)

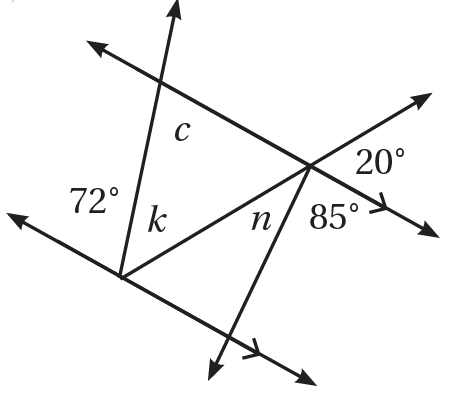
$\mathbf{m}\mathbf{\angle }\mathbf{c}\mathbf{=}72°$                               متبادلة داخليا مع زاوية قياسها °72 والتبادل ناتج عن قاطع لمتوازيين.

$$\begin{gathered} \mathbf{m}\mathbf{\angle }\mathbf{n}\mathbf{=}180°-\left(20+85\right)° \\ \mathbf{m}\mathbf{\angle }\mathbf{n}\mathbf{=}75° \end{gathered}$$                               متكاملة مع زاويتين قياسهما °20 وَ °85

$$\begin{gathered} \mathbf{m}\mathbf{\angle }\mathbf{k}\mathbf{=}180°-\left(20+72\right)° \\ \mathbf{m}\mathbf{\angle }\mathbf{k}\mathbf{=}88° \end{gathered}$$                               قياس الزاوية المجاورة للزاوية k يساوي °20 ، لأنها تناظر زاوية قياسها °20

 

في الشكلِ المُجاوِرِ، أجدُ قياسَ كُلٍّ منَ الزّوايا الآتية:

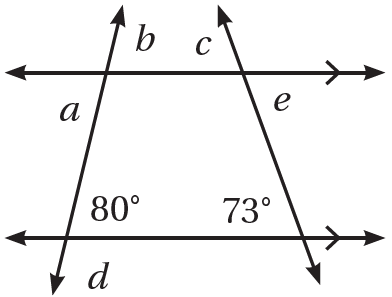
9) $\mathbf{m}\mathbf{\angle }\mathbf{a}\mathbf{=}80°\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{m}\mathbf{\angle }\mathbf{b}\mathbf{=}80°$                   الزاوية b بالتناظر ، والزاوية a متبادلة داخلياً 

10) $\mathbf{m}\mathbf{\angle }\mathbf{c}\mathbf{=}73° \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{m}\mathbf{\angle }\mathbf{e}\mathbf{=}73°$                   الزاوية c بالتناظر ، والزاوية e متبادلة داخلياً 

11) $$\begin{gathered} \mathbf{m}\mathbf{\angle }\mathbf{d}\mathbf{=}180°-80° \\ \mathbf{m}\mathbf{\angle }\mathbf{d}\mathbf{=}100° \end{gathered}$$                                  زاويتيين متكاملتين