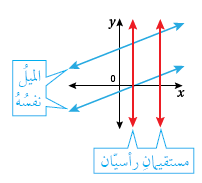
يُسمّى المستقيمانِ الواقعانِ في المستوى نفسِه ولا يقطعُ أحدُهُما الآخرَ مستقيمينِ متوازيينِ ويكونُ لهُما الميلُ نفسُه. والمستقيماتُ الرأسيةُ جميعُها متوازيةٌ.
مثال(1):
أكتبُ بصيغةِ الميلِ والمقطعِ معادلةَ المستقيمِ المارِّ بالنقطةِ والموازي للمستقيمِ
1) المستقيمان المتوازيان لهما نفس الميل وعليه فميل كل من المستقيمين يساوي
2) بصيغة الميل والنقطة:
3) نحول إلى صيغة الميل والمقطع:
يُسَمّى المستقيمانِ اللذانِ يتقاطعانِ مُكوِّنَينِ زوايا قوائمَ
مستقيمينِ متعامدينِ. ويكونُ ميلُ أحدِهِما معكوسَ مقلوبِ مَيلِ الآخرِ، وهذا يعني أنَّ حاصلَ ضربِ مَيْلَيْهِما يساوي والمستقيماتُ الرأسيّةُ والأفقيّةُ متعامِدةٌ.
مثال(2):
أكتبُ بصيغةِ الميلِ والمقطعِ معادلةَ المستقيمِ المارِّ بالنقطةِ ( 0 , 4) والعموديِّ على المستقيمِ
1) ميل المستقيم المعطى
الميل يساوي
2) ميلَ المستقيمِ العموديِّ على المستقيمِ المُعْطى.
3) معادلةَ المستقيمِ
يمكنُ تحديدُ ما إذا كانَ المستقيمانِ متوازيينِ أو متعامِدينِ أو غيرَ ذلكَ منْ خلالِ الميلِ.
مثال(3):
1) أحدّدُ ما إذا كانَ المستقيمانِ و متوازيينِ أو متعامدينِ أو غيرَ ذلكَ.
أ) ميل المستقيم
الميل يساوي
ب) ميل المستقيم يساوي
نلاحظ بأن الميل متساوي لذا فهما متوازيين
2) أحدّدُ ما إذا كانَ و متوازيينِ أو متعامِدينِ أو غيرَ ذلكَ، حيثُ
أ) ميل
ب) ميل
ج) المَيْلانِ غيرُ متساويينِ، إذنْ، فالمستقيمانِ غيرُ متوازيينِ. ولتحديدِ ما إذا كان المستقيمانِ متعامِدينِ أجدُ حاصلَ ضربِ مَيْلَيْهِما
بما أن حاصل ضرب ميليهما يساوي ، فالمستقيمان متعامدان
يمكنُ كتابةُ معادلةِ أيِّ مستقيمٍ يمرُّ بنقطةٍ معلومةٍ يوازي أو يعامِدُ مستقيمًا معلومًا في كثيرٍ منَ التطبيقاتِ الحياتيّةِ.
مثال(4):
عمارةٌ: ترغبُ إحدى البلدياتِ بربطِ مدخلِ الحديقةِ العامةِ بمسارِ 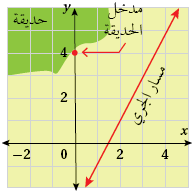
أ) أجدُ ميلَ المستقيمِ الذي يمثلُ مسارَ الجريِ. تقعُ النقطتانِ
( 1 , 2), (5 , 4) على مسارِ الجريِ، إذنْ، يمكنُ منْ خلالِهما إيجادُ ميلِ المستقيمِ الذي يمثّلُ المسارَ.
ب) بما أنَّ الممرَّ عموديٌّ على مسارِ الجريِ، إذنْ، أجدُ مقلوبَ معكوسِ ميلِ مسارِ الجريِ. بما أنَّ ميلَ مسارِ الجريِ يساوي 2، فإنَّ مقلوبَ معكوسِه
ج) بما أنَّ المستقيمَ الذي يمثلُ المَمرَّ يقطعُ المحورَ y في النقطةِ ( 4 , 0)، إذنْ، فإنَّ المقطعَ y لهُ يساوي 4، وعليهِ فإنَّ معادلةَ الممرِّ بصيغةِ الميلِ والمقطعِ هيَ: