المعادلةُ الخطيّةُ بالصورةِ القياسيّةِ

المعادلةُ الخطّيّةُ هيَ المعادلةُ التي يمكنُ كتابتُها على الصورةِ Ax + By = C ، وتُسمّى الصورةَ القياسيةَ Standard form للمعادلةِ الخطّيّةِ.

الصورةُ القياسيّةُ للمعادلةِ الخطّيّةِ هي:   Ax + By = C حيثُ A ≥ 0 ، ولا تكونُ قيمتا A و B معًا صفرًا، حيثُ A, B, C أعدادٌ صحيحةٌ، العاملُ المشتركُ الأكبرُ لها 1.

مثال(1)

أُحدّدُ ما إذا كانتْ كلُّ معادلةٍ ممّا يأتي خطّيّةً أَمْ لا، وإذا كانتْ كذلكَ أكتبُها على الصورةِ القياسيةِ.

1) y = 6 - 5x

أعيدُ كتابةَ المعادلةِ بحيثُ يكونُ كِلا المتغيرينِ في الطَّرفِ نفسِه منَ المعادلةِ.

المعادلةُ الأصليةُ                                      y = 6 - 5x
أُضيفُ 5x إلى طرفَِ المعادلةِ                      y + 5x = 6 - 5x + 5x
أُبسّطُ                                          5x+y=6

المعادلةُ 5x + y = 6 معادلةٌ خطيّةٌ بالصورةِ القياسيةِ، حيثُ. A=5, B=1, C=6 

2) 3xy - 4x = 7

بما أنَّ الحدّ 3xy فيهِ متغيرانِ، فإنَّه لا يمكنُ كتابةُ المعادلةِ على الصورةِ Ax + By = C ، إذنْ فالمعادلةُ ليستْ خطيّةً.

3) 4x - 8y = 12

بما أنَّ العاملَ المشتركَ الأكبرَ للأعدادِ 4 و 8 و 12 ليسَ 1، فإنَّ المعادلةَ ليستْ مكتوبةً بالصورةِ القياسيةِ. ولِكتابتِها بالصورةِ القياسيةِ؛ أقسمُ كلَّ طرفٍ على ع. م . أ للأعدادِ 4 وَ 8 وَ 12

المعادلةُ الأصليةُ                                    $4x - 8y =12$
أجدُ (ع. م. أ) وهو 4                                 $4(x-2y) = 12$
أقسمُ طَرفَِ المعادلةِ على 4                $\frac{4(x-2y) }{4}=\frac{12}{4}$
أُبسّطُ                                                            $x -2y = 3$

إذنْ، فالمعادلةُ $x-2y = 3$ خطيّةٌ مكتوبةٌ بالصورةِ القياسيةِ، حيثُ .$A = 1, B =-2, C =3$

4) $\frac{7}{5} x=-4$

لتحويلِ معاملاتِ المعادلةِ إلى أعدادٍ صحيحةٍ، أضربُ طرفَيِ المعادلةِ في 5 

المعادلةُ الأصليةُ                                   $\frac{7}{5} x=-4$

أضربُ طَرفَِ المعادلةِ في 5                 $5\times \left(\frac{7}{5}\right) x=5(-4)$

أُبسّطُ                                                       $7x = -20$

ويمكنُ كتابةُ المعادلةِ $7x = -20$ بالصورةِ القياسيةِ وهيَ: $7x + 0y = -20$
إذنْ، فالمعادلةُ خطيّةٌ بالصورةِ القياسيةِ، حيثُ $A = 7, B = 0, C = -20$

التمثيلُ البيانيُّ للمعادلةِ الخطيّةِ هو مستقيمٌ يمرُّ في الأزواجِ المُرتّبةِ جميعِها التي تمثّلُ حلولاً للمعادلةِ، وأيُّ زوجٍ مرتَّبٍ يقعُ على هذا المستقيمِ يمثّلُ حلاً للمعادلةِ.

مثال(2)

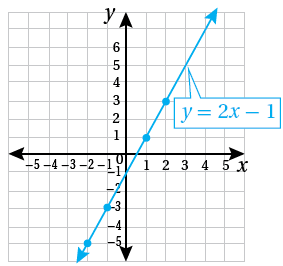
1) أمثِّلُ المعادلةَ $2x - y = 1$ بيانيًّا.

الْخُطْوَةُ(1): أكتبُ المعادلةَ بدلالةِ y لتسهيلِ عمليةِ إيجادِ قيمِ y المقابلةِ لقيمِ $x$

المعادلةُ الأصليةُ                                                 $2x - y = 1$

اطرح $2x$ من كِلا الطرفينِ                            $2x - y - 2x = 1 - 2x$

أقسمُ طَرفَِ المعادلةِ على $-1$  وأبسط                  $y=2x-1$

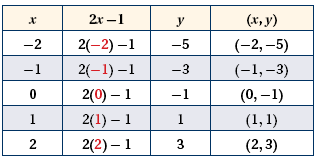
الْخُطْوَةُ(2): أُنشئُ جدولَ قيمٍ. 

أختارُ قيمًا للمتغيرِ $x$، ثمَّ أعوِّضُها في المعادلةِ لأجدَ قيمَ $y$ المقابِلةَ لها.

الْخُطْوَةُ(3): أمثّلُ الأزواجَ المُرتَّبةَ في المستوى الإحداثيِّ، ثمَّ أرسمُ مستقيمًا يمرُّ بها جميعًا. 

 

 

 

 

 

 

 

بما أنَّهُ يمكنُ تمثيلُ المستقيمِ بنقطتينِ، فإنَّ أسهلَ طريقةٍ لتمثيلِ المعادلةِ الخطيّةِ هي إيجادُ نقطتَيْ تقاطعِ المستقيمِ معَ المحورينِ الإحداثيّينِ إِنْ أمكنَ.يُسمّى الإحداثيُّ $\mathit{x}$ للنقطةِ التي يقطعُ عندَها المستقيمُ المحورَ $\mathit{x}$  المقطعَ $\mathit{x}$ (X-intercept)، ويُسمّى الإحداثيُّ y للنقطةِ التي يقطعُ عندَها المستقيمُ المحورَ $\mathit{y}$ المقطعَ $\mathit{y}$ (y-intercept).

مثال(3)

أمثّلُ كلَّ معادلةٍ ممّا يأتي بيانيًّا باستعمالِ المقطعِ x والمقطعِ :y

1) $3x-2y=6$

الْخُطْوَةُ(1): أجدُ المقطعَ $x$ والمقطعَ$y$.

المقطع $x$:

المعادلةُ الأصليةُ                                                     $3x-2y=6$

أعوض $y=0$                                                       $3x - 2 \left(0\right) = 6$

أقسمُ كِلا الطرفينِ على 3                                    $\frac{3x}{3}=\frac{6}{3}$

وأبسط                                                                       $x=2$

 

المقطع $y$:

المعادلةُ الأصليةُ                                            $3x-2y=6$

أعوض $x=0$                                                 $3\left(0\right)-2y=6$

أقسمُ كِلا الطرفينِ على $-2$                        $\frac{-2y}{-2}=\frac{6}{-2}$

وأبسط                                                           $y=-3$         

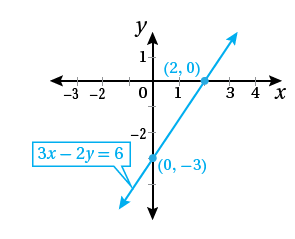
الْخُطْوَةُ(2): أُمثّلُ نقطتَيْ تقاطعِ المستقيمِ معَ المحورينِ الإحداثيّينِ في المستوى الإحداثيِّ، ثمَّ أرسمُ مستقيمًا يصلُ بينَ النقطتينِ. 

بما أنَّ المقطعَ $x$ هُوَ 2، فإنَّ المستقيمَ يقطعُ المحورَ $x$ في النقطةِ $( 2 , 0)$، وبما
أنَّ المقطعَ$y$ هو $-3$، فإنَّ المستقيمَ يقطعُ المحورَ $y$ في النقطةِ $( 0, -3)$، أُمثّلُ
النقطتان في المستوى الإحداثيِّ، ثمَّ أرسمُ مستقيمًا يصلُ بينَهُما.

 

 

2) $y = 3$

 الْخُطْوَةُ(1): أكتبُ المعادلةَ بالصورةِ القياسيةِ.

$0x+1y=3$

الْخُطْوَةُ(2): أجدُ المقطعَ x والمقطعَ y. 

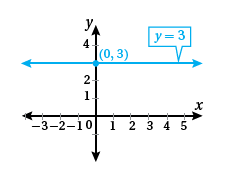
أُلاحظُ أنَّ المقطعَ y هو 3، ولا يوجدُ مقطعُ x،
وأُلاحظُ أيضًا أنَّ قيمةَ y = 3 لأيِّ قيمةِ x؛ لذا فإنَّ التمثيلَ البيانيَّ للمعادلةِ y = 3 هو مستقيمٌ أفقيٌّ يقطعُ المحورَ y في النقطةِ ( 3 , 0).

 

 

3) $x=-2$

الْخُطْوَةُ(1): أكتبُ المعادلةَ بالصورةِ القياسيةِ.

$1x+0y=-2$

الْخُطْوَةُ(2): أجدُ المقطعَ x والمقطعَ y. 

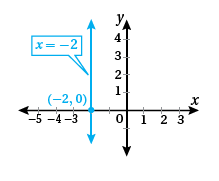
أُلاحظُ أنَّ المقطعَ x هو 2-، ولا يوجدُ مقطعُ y،
وألاحظُ أيضًا أنَّ قيمةَ x = -2 لأيِّ قيمةِ y؛ لذا فإنَّ التمثيلَ البيانيَّ للمعادلةِ x = -2 هو مستقيمٌ رأسيٌّ يقطعُ المحورَ x في النقطةِ ( 0 , 2-).

 

مثال(4)

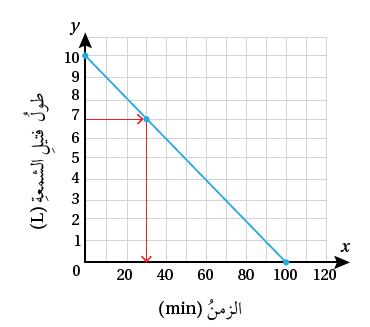
شمعةٌ: يبيّنُ التمثيلُ البيانيُّ المجاورُ العلاقةَ بينَ طولِ فتيلِ شمعةٍ بالسنتيمتراتِ والزمنِ بالدقائقِ منذُ بدءِ إشعالِه.

1) أجدُ المقطعَ x والمقطعَ y للعلاقةِ.

المقطعُ x هو 100             قيمةُ x =100 عندَما قيمةُ y = 0
المقطعُ y هو 10                قيمةُ y =10 عندَما قيمةُ x = 0   

2) أصفُ مدلولَ كلٍّ منَ المقطعينِ في هذهِ الحالةِ.

المقطعُ y يساوي 10 ويعني أنَّ طولَ فتيلِ الشمعةِ  $10 cm$ عندَ إشعالِه، المقطعُ x يساوي 100 ، وهذا يعني أنَّ فتيلَ الشمعةِ احترقَ احتراقًا كاملاً بعدَ 100 دقيقةٍ، ولم يبقَ منهُ شيءٌ

3) بعدَ كمْ دقيقةٍ يكونُ طولُ فتيلِ الشمعةِ $7 cm$ ؟

أُحدّدُ $7 cm$ على المحورِ y، ثمَّ أُحدّدُ النقطةَ التي
تقابلُها على المستقيمِ، وأحدّدُ الإحداثيَّ x للنقطةِ وهو 30. إذنْ، يكونُ طولُ فتيلِ الشمعةِ $7 cm$ بعدَ 30 دقيقةً منْ إشعالِه