رياضيات10 فصل أول

أتحقق من فهمي صفحة 79 

أحدد إذا كانت الزاويتان الآتيتان في وضع قياسي أم لا ، مبينًا السبب : 

$x \mathrm{المحور} \mathrm{على} \mathrm{منطبق} \mathrm{الابتداء} \mathrm{وضلع،} \mathrm{الاصل} \mathrm{نقطة} \mathrm{في} \mathrm{راسها} \mathrm{لان؛} \mathrm{القياسي} \mathrm{الوضع} \mathrm{في} \mathrm{الزاوية}$

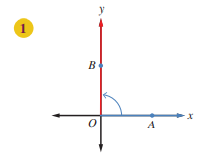
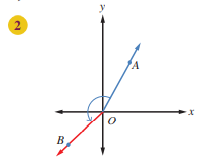
الزاوية ليست في الوضع القياسي لأن ضلع الإبتداء لا ينطبق على محور السينات الموجب. 

---

أتحقق من فهمي صفحة 80 

ارسم زاوية قياسها $460°$ في الوضع القياسي ، محددًا مكانها .

في الربع الثاني 

---

أتحقق من فهمي صفحة 81

أجد النسب المثلثية الأساسية للزاوية $\theta$المرسومة في الوضع القياسي ، التي يقطع ضلع انتهائها دائرة الوحدة عند النقطة $P(- \frac{\sqrt[]{2}}{2} ,- \frac{\sqrt[]{2}}{2})$

$sin \theta =y=-\frac{\sqrt[]{2}}{2}$

$cos \theta =x=-\frac{\sqrt[]{2}}{2}$

$tan \theta =\frac{-\frac{\sqrt[]{2}}{2}}{-\frac{\sqrt[]{2}}{2}}=-\frac{\sqrt[]{2}}{2}\times -\frac{\sqrt[]{2}}{2}=1$

---

أتحقق من فهمي صفحة 82

أجد النسب المثلثية الأساسية للزاويتين اللتين قياس كل منهما $270°$ و $360°$ على الترتيب . 

$sin 270°=-1,cos 270°=0,tan 270°=\mathrm{معرفة} \mathrm{غير} \mathrm{قيمة}$

$sin 360°=0,cos 360°=1,tan 360°=0$

---

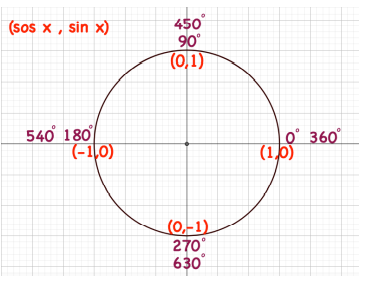
أتحقق من فهمي صفحة 84

$$\begin{gathered} \mathrm{أجد} \mathrm{قيمة} \mathrm{كل} \mathrm{من} \theta \sin و \theta \tan \mathrm{إذا} \mathrm{كان} 8.0 = \theta \cos ، \\ \mathrm{ووقع} \mathrm{ضلع} \mathrm{انتهاء} \theta \mathrm{في} \mathrm{الوضع} \mathrm{القياسي} \mathrm{في} \mathrm{الريع} \mathrm{الرايع} \end{gathered}$$

$cos\theta =0.8$

${\left(sin\theta \right)}^2+{\left(cos\theta \right)}^2=1$

${\left(sin\theta \right)}^2+{\left(\frac{8}{10}\right)}^2=1$

${\left(sin\theta \right)}^2=\frac{100}{100}-\frac{64}{100}=\frac{36}{100}$

$sin\theta =\pm \frac{6}{10}$

$\mathrm{فان} \mathrm{الرابع} \mathrm{الربع} \mathrm{في} \theta \mathrm{لان}$

$sin\theta =-\frac{6}{10}$

$tan \theta =\frac{sin \theta }{cos \theta }=\frac{\frac{-6}{10}}{\frac{8}{10}}=\frac{-6}{10}\times \frac{10}{8}=\frac{-6}{8}=\frac{-3}{4}$

---

أتدرب وأحل المسائل

أرسم الزوايا الآتية في الوضع القياسي : 

$1. 225°$

$2. 160°$

$3. 330°$

$4. 240°$

---

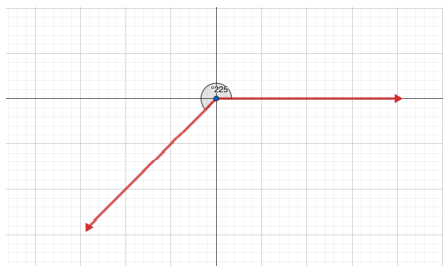
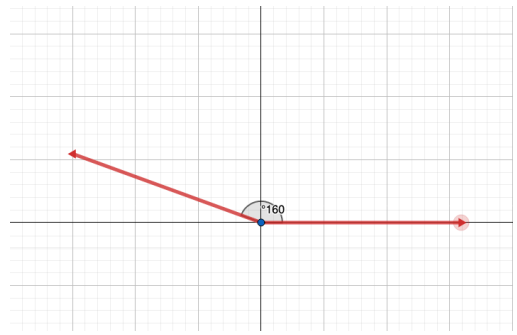
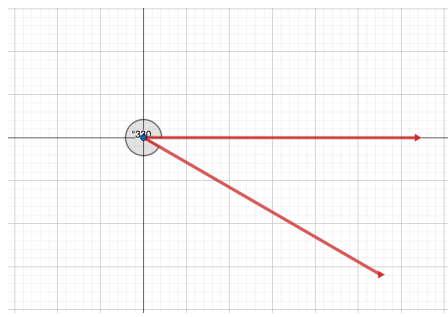
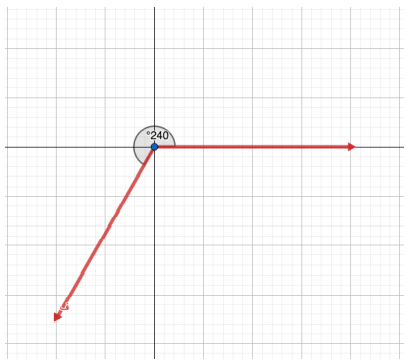
أحدد الربع الذي يقع فيه ضلع انتهاء كل زاوية مما يأتي إذا رسمت في الوضع القياسي : 

$5. 285° \mathrm{الرابع} \mathrm{الربع}$

$6. 75° \mathrm{الاول} \mathrm{الربع}$

$7. 100° \mathrm{الثاني} \mathrm{الربع}$

$8. 265° \mathrm{الثالث} \mathrm{الربع}$

---

أحدد الربع ( أو الأرباع) الذي يقع فيه ضلع انتهاء الزاوية $\theta$ في الوضع القياسي إذا كان : 

$9. sin\theta >0$

$\mathrm{الاول} \mathrm{الربع} و \mathrm{الثاني} \mathrm{الربع}$

$10. cos\theta >0$

$\mathrm{الاول} \mathrm{الربع} و \mathrm{الرابع} \mathrm{الربع}$

$11. tan\theta <0$

$\mathrm{الثاني} \mathrm{الربع} و \mathrm{الرابع} \mathrm{الربع}$

$12. \sin \theta <0 و \cos \theta <0$

$\mathrm{الثالث} \mathrm{الربع}$

---

أحدد الربع ( أو الأرباع ) الذي يقع فيه ضلع انتهاء الزاوية $\theta$  في الوضع القياسي إذا كان: 

$13. sin\theta =-0.7$

$\mathrm{الثالث} \mathrm{الربع} و \mathrm{الرابع} \mathrm{الربع}$

$14. tan\theta =2$

$$\begin{gathered} \mathrm{الاول} \mathrm{الربع} و \mathrm{الثالث} \mathrm{الربع} \\ 15. cos \theta =-\frac{1}{2} \\ \mathrm{الثاني} \mathrm{الربع} و \mathrm{الثالث} \mathrm{الربع} \end{gathered}$$

$16. tan\theta =-1$

$\mathrm{الثاني} \mathrm{الربع} و \mathrm{الرابع} \mathrm{الربع}$

$17. cos\theta =0.45$

$\mathrm{الاول} \mathrm{الربع} و \mathrm{الرابع} \mathrm{الربع}$

$18. sin\theta =0.55$

$\mathrm{الاول} \mathrm{الربع} و \mathrm{الثاني} \mathrm{الربع}$

$19. sin\theta =0.3,cos\theta <0$

$\mathrm{الثاني} \mathrm{الربع}$

$20. tan\theta =-4,sin\theta >0$

$\mathrm{الثاني} \mathrm{الربع}$

---

أجد النسب المثلثية الأساسية للزاوية $\theta$ إذا قطع ضلع انتهائها في الوضع القياسي دائرة الوحدة في النقاط الآتية : 

$21 .P(0 ,-1)$

$sin\theta =y=-1,cos\theta =x=0$

$tan\theta =\frac{sin\theta }{cos\theta }=\frac{-1}{0}\mathrm{معرفة} \mathrm{غير} \mathrm{قيمة}$

 

$22. P(0.5,0.5 \sqrt[]{3})$

$sin\theta =y=0.5\sqrt[]{3},cos \theta =x=0.5$

$tan\theta =\frac{sin \theta }{cos \theta }=\frac{0.5\sqrt[]{3}}{0.5}=\sqrt[]{3}$

 

$23. P(-\frac{8}{17},\frac{15}{17})$

$sin\theta =y=\frac{15}{17},cos\theta =x=\frac{-8}{17}$

$tan\theta =\frac{sin \theta }{cos \theta }=\frac{\frac{15}{17}}{\frac{-8}{17}}=\frac{15}{17}\times \frac{17}{-8}=\frac{15}{8}$

 

$24. P(\frac{20}{29},-\frac{21}{29})$

$sin\theta =y=\frac{-21}{29},cos \theta =x=\frac{20}{29}$

$tan\theta =\frac{sin \theta }{cos \theta }=\frac{\frac{-21}{29}}{\frac{20}{29}}=\frac{-21}{29}\times \frac{29}{20}=\frac{-21}{20}$

---

أجد النسبتين المثلثتين الأساسيتين الباقيتين في الحالات الآتية : 

$25. sin\theta =\frac{3}{4}, 90°<\theta <180°$

$\mathrm{الثاني} \mathrm{الربع} \mathrm{في} \theta \mathrm{الزاوية}$

$sin\theta =\frac{3}{4}$

${\left(sin\theta \right)}^2+{\left(cos\theta \right)}^2=1$

${\left(\frac{3}{4}\right)}^2+{(cos \theta )}^2=1$

$\frac{9}{16}+{(cos \theta )}^2=1$

${\left(cos\theta \right)}^2=1-\frac{9}{16}=\frac{7}{16}$

$cos\theta =\pm \frac{\sqrt[]{7}}{4}$

$\mathrm{فان} \mathrm{الثاني} \mathrm{الربع} \mathrm{في} \theta \mathrm{لان}$

$cos\theta =-\frac{\sqrt[]{7}}{4}$

$tan\theta =\frac{sin \theta }{cos \theta }=\frac{\frac{3}{4}}{-\frac{\sqrt[]{7}}{4}}=\frac{3}{4}\times -\frac{4}{\sqrt[]{7}}=\frac{-3}{\sqrt[]{7}}$

 

$26. tan\theta =0.78, -1<sin\theta <0$

$\mathrm{الثالث} \mathrm{الربع} \mathrm{في} \theta \mathrm{الزاوية}$

$tan\theta =\frac{sin\theta }{cos\theta }=\frac{78}{100}=\frac{36}{50}=\frac{18}{25}$

$\mathrm{تبادلي} \mathrm{ضرب}$

$25sin\theta =18cos\theta$

$sin\theta =\frac{18}{25} cos\theta$

${\left(sin\theta \right)}^2+{\left(cos\theta \right)}^2=1$

${(\frac{18}{25} cos\theta )}^2+{\left(cos\theta \right)}^2=1 \frac{324}{625}{\left(cos\theta \right)}^2+{\left(cos\theta \right)}^2=1$

$324{\left(cos\theta \right)}^2+625{(cos \theta )}^2=625$

$949{\left(cos\theta \right)}^2=625$

${\left(cos\theta \right)}^2=\frac{625}{949}$

$cos\theta =\pm \sqrt[]{\frac{625}{949}}$

$\mathrm{الثالث} \mathrm{الربع} \mathrm{في} \theta \mathrm{الزاوية} \mathrm{لان}$

$cos\theta =-\sqrt[]{\frac{625}{949}}=-\frac{25}{\sqrt[]{949}}\approx -0.812$

$sin\theta =\frac{18}{25} cos\theta$

$sin\theta =\frac{18}{25}\times -0.812\approx -0.585$

 

$27. cos\theta =- .075,tan\theta <0$

$\mathrm{الثاني} \mathrm{الربع} \mathrm{في} \theta \mathrm{الزاوية}$

$cos\theta =\frac{-75}{100}=\frac{-3}{4}$

${(sin \theta )}^2+{(\cos \theta )}^2=1$

${\left(sin\theta \right)}^2+{\left(\frac{-3}{4}\right)}^2=1$

${\left(\sin \theta \right)}^2+\frac{9}{16}=1$

${(sin \theta )}^2=1-\frac{9}{16}=\frac{7}{16}$

$sin\theta =\pm \sqrt[]{\frac{7}{16}}$

$\mathrm{فان} \mathrm{الثاني} \mathrm{الربع} \mathrm{في} \theta \mathrm{لان}$

$\sin \theta =+\frac{\sqrt[]{7}}{4}$

$tan \theta =\frac{sin \theta }{cos \theta }=\frac{\frac{\sqrt[]{7}}{4}}{\frac{-3}{4}}=\frac{\sqrt[]{7}}{4}\times \frac{-4}{3}=\frac{\sqrt[]{7}}{3}\approx -0.88$

 

$28. sin\theta =-0.87 , 270°<\theta <360°$

$\mathrm{الرابع} \mathrm{الربع} \mathrm{في} \theta \mathrm{الزاوية}$

$\sin \theta =\frac{-87}{100}$

${(\sin \theta )}^2+{(\cos \theta )}^2=1$

${\left(\frac{-87}{100}\right)}^2+{\left(\cos \theta \right)}^2=1$

$\frac{7569}{10000}+{(\cos \theta )}^2=1$

${(\cos \theta )}^2=1-\frac{7569}{10000}=\frac{2431}{10000}$

$\cos \theta =\pm \frac{\sqrt[]{2431}}{100}$

$\mathrm{فان} \mathrm{الرابع} \mathrm{الربع} \mathrm{في} \theta \mathrm{لان}$

$\cos \theta \approx +\frac{49}{100}=0.49$

$\tan \theta =\frac{\sin \theta }{\cos \theta }=\frac{\frac{-87}{100}}{\frac{49}{100}}=\frac{-87}{100}\times \frac{100}{49}=\frac{-87}{49}\approx -1.78$

---

مهارات التفكير العليا 

29. تبرير : ما أكبر قيمة لجيب الزاوية ؟ ما أصغر قيمة له ؟ أبرر إجابتي 

الحل:

اكبر قيمة لجيب الزاوية هي 1، وعندئذ يكون قياس الزاوية هو °90، واصغر قيمة هي 1-، وعندئذ يكون قياس الزاوية هو °270؛ لان ضلع انتهاء الزاوية °90 يقطع دائرة الوحدة عند النقطة (0,1) وضلع انتهاء الزاوية °270 يقطع دائرة الوحدة عند النقطة (1,0-)

---

30 . اكتشف الخطأ : حل كل من أمجد وزينة المسألة الآتية . إذا كان $\tan x = 0.75$، وكانت x بين$180°$ و $360°$  ، فما قيمة $\sin x + \cos x$ ؟ 

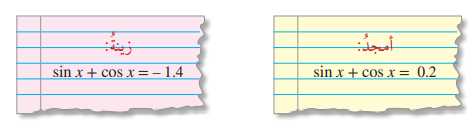
أحدد أيهما كانت إجابته صحيحة ، مبررا إجابتي . 

الحل :

الزاوية × في الربع الثالث بالتالي كل من sin x و cos x قيم سالبة وبالتالي مجموعهما قيمة سالبة بالتالي حل زينة هو الصحيح

---

كتاب التمارين : 

ارسم الزوايا الآتية في الوضع القياسي 

$1. 170°$

$2. 240°$

$3. 315°$

$4. 85°$

---

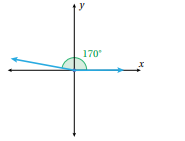
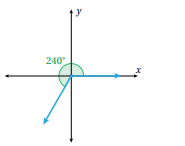
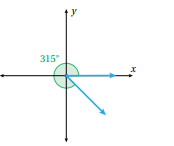
أحدد الربع الذي يقع فيه ضلع انتهاء كل زاوية مما يأتي إذا رسمت في الوضع القياسي : 

5. 245°
الربع الثالث
6. 275°
الربع الرابع
7. 130°
الربع الثاني
8. 26°
الربع الأول

---

أجد النسب المثلثية الأساية للزاوية $\theta$ إذا قطع ضلع انتهائها في الوضع القياسي دائرة الوحدة في النقطة: 

$9. P(0,-1)$

$\mathit{s}\mathit{i}\mathit{n}\mathbf{ }\mathit{x}\mathbf{=}\mathbf{-}\mathbf{1}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{cos}\mathit{x}\mathbf{=}\mathbf{0}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{ }\mathit{t}\mathit{a}\mathit{n}\mathit{x}\mathbf{ }\mathbf{ }\mathit{u}\mathbf{.}\mathit{d}\mathbf{ }$

 

$10. P(1,0)$

$\mathit{s}\mathit{i}\mathit{n}\mathit{x}\mathbf{=}\mathbf{0}\mathbf{,}\mathbf{ }\mathbf{cos}\mathit{x}\mathbf{=}\mathbf{1}\mathbf{,}\mathbf{ }\mathit{t}\mathit{a}\mathit{n}\mathit{x}\mathbf{=}\mathbf{0}\mathbf{ }$

 

$11. P(\frac{8}{17} ,-\frac{15}{17})$

$\mathit{s}\mathit{i}\mathit{n}\mathit{x}\mathbf{=}\mathbf{-}\frac{\mathbf{15}}{\mathbf{17}}\mathbf{,}\mathit{c}\mathit{o}\mathit{s}\mathit{x}\mathbf{=}\mathbf{-}\frac{\mathbf{8}}{\mathbf{17}}\mathbf{ }\mathbf{,}\mathit{t}\mathit{a}\mathit{n}\mathit{x}\mathbf{=}\mathbf{-}\frac{\mathbf{15}}{\mathbf{8}}$

 

$12. P (-\frac{60}{61},-\frac{11}{61})$

$\mathit{s}\mathit{i}\mathit{n}\mathit{x}\mathbf{=}\mathbf{-}\frac{\mathbf{11}}{61}\mathbf{,}\mathit{c}\mathit{o}\mathit{s}\mathit{x}\mathbf{=}\frac{\mathbf{-}\mathbf{60}}{\mathbf{61}}\mathbf{,}\mathit{t}\mathit{a}\mathit{n}\mathit{x}\mathbf{ }\mathbf{=}\frac{11}{60}\mathbf{ }$

 

---

أحدد الربع ( أو الأرباع ) الذي يقع فيه ضلع انتهاء الزاوية $\theta$ في الوضع القياسي إذا كان : 

$\mathbf{13}\mathbf{.}\mathbf{ }\mathit{s}\mathit{i}\mathit{n}\mathit{\theta }\mathbf{<}\mathbf{0}$

الربع الثالث أو الربع الرابع

$\mathbf{14}\mathbf{.}\mathit{c}\mathit{o}\mathit{s}\mathit{\theta }\mathbf{<}\mathbf{0}$

الربع الثاني ، أو الربع الثالث

$\mathbf{15}\mathbf{.}\mathit{c}\mathit{o}\mathit{s}\mathit{\theta }\mathbf{<}\mathbf{0}\mathbf{,}\mathbf{ }\mathit{t}\mathit{a}\mathit{n}\mathit{\theta }\mathbf{>}\mathbf{0}$

الربع الثالث

$\mathbf{16}\mathbf{.}\mathbf{ }\mathit{t}\mathit{a}\mathit{n}\mathit{\theta }\mathbf{<}\mathbf{0}\mathbf{,}\mathbf{ }\mathit{c}\mathit{o}\mathit{s}\mathit{\theta }\mathbf{<}\mathbf{0}$

الربع الثاني

---

أجد النسبتين المثلثيتين الأساسيتين الباقيتين في كل من الحالات الآتية : 

$17. cos\theta =-\frac{1}{2}, 90°<\theta <180°$

${\mathbf{sin}}^2\theta +co{s}^2\theta =1$

$si{n}^2\theta +{\left(\frac{-1}{2}\right)}^2=1\Rightarrow si{n}^2\theta =1-\frac{1}{4}=\frac{3}{4}$

$sin\theta =\frac{\sqrt[]{3}}{2}\Rightarrow tan \theta =-\sqrt[]{3}$

 

$18. tan\theta =-2, -1<sin\theta <0$

$\frac{sin\theta }{cos\theta }=-2\Rightarrow sin\theta =-2cos\theta$

$si{n}^2\theta +co{s}^2\theta =1\Rightarrow {(-2cos\theta )}^2+co{s}^2\theta =1$

$5co{s}^2\theta =1\Rightarrow cos \theta =\frac{1}{\sqrt[]{5}}\Rightarrow sin \theta =\frac{-2}{\sqrt[]{5}}$

 

$19. sin\theta =0.6,tan\theta <0$

$si{n}^2\theta +co{s}^2\theta =1\Rightarrow {(0.6)}^2+co{s}^2\theta =1\Rightarrow co{s}^2\theta =0.64$

$cos\theta =-0.8\Rightarrow tan\theta =\frac{0.6}{-0.8}=\frac{-3}{4}=-0.75$

 

$20.cos\theta =0.45, 270°<\theta <360°$

$si{n}^2\theta +co{s}^2\theta =1\Rightarrow si{n}^2\theta =1-{(0.45)}^2\Rightarrow sin\theta \approx -0.89$

$tan\theta \approx -1.98$

---

جلس زيد في لعبة الدولاب على المقعد  الذي تمثله النقطة ( 1 ,0)  على دائرة الوحدة . إذا كان الدولاب يدور عكس حركة عقارب الساعة، ويكمل دورة واحدة في دقيقتين : 

21. فما إحداثيا النقطة على دائرة الوحدة التي تمثل مقعد زيد بعد 60 ثانية ؟ 

$\mathit{P}\mathbf{(}\mathbf{0}\mathbf{,}\mathbf{-}\mathbf{1}\mathbf{)}\mathbf{ }$

22. فما إحداثيا النقطة على دائرة الوحدة التي تمثل مقعد زيد بعد 90 ثانية ؟ 

$\mathit{P}\mathbf{(}\mathbf{1}\mathbf{,}\mathbf{0}\mathbf{)}$

---