رياضيات فصل أول

النهايات والاتصال

إيجاد النهايات بيانيا وعدديا:

سنتعلم في هذا الدرس تحليل سلوك اقتران معطى ومع تحديد إذا كانت قيم الاقتران تقترب أكثر فأكثر من عدد ما كل ما اقتربت قيم x أكثر فأكثر من عدد محدد مثل c حينها نستطيع تسمية العدد التي تقترب منه قيم الاقتران بالنهاية.

إذا كانت قيمة الاقتران f(x) تقترب من قيمة واحدة L عندما تقترب x من c؛ فإن نهاية f(x) عندما تقترب xمن c هي L. $\underset{x\to c}{\lim }f\left(x\right)=L$ نهاية الاقتران f(x) عندما تقترب x من c هي L.

ملاحظات:

عند كتابة $\underset{x\to c}{\lim }f\left(x\right)$ فهذا يشير إلى أن x تقترب من c من جهتي اليمين واليسار إذا أردنا تحديد الجهة التي تقترب منها قيم x من القيمة c.

1) استعمل $\underset{x\to c^{-}}{\lim }f\left(x\right)$ لدلالة على النهاية من جهة اليسار حيث x<c وتقرأ: نهاية f(x) عندما تقترب x من c من اليسار.

2) استعمل $\underset{x\to c^{+}}{\lim }f\left(x\right)$ لدلالة على النهاية من جهة اليمين حيث x>c وتقرأ: نهاية f(x) عندما تقترب x من c من اليمين.

مع مراعاة أن نهاية الاقتران f(x) تكون موجودة عندما تقترب x من c إذا كانت النهايتان من اليمين واليسار موجودتين ومتساويتين.

تكون النهاية f(x) موجودة عندما تقترب x من c، إذا وفقط إذا كانت النهايتان من اليمين واليسار موجودتين ومتساويتين. $\underset{x\to c}{lim}f\left(x\right)=\underset{x\to c^{+}}{lim}f\left(x\right)=L \mathrm{إذا} \mathrm{وفقط} \mathrm{إذا} \underset{x\to c}{lim}f\left(x\right)=L$

 

ملاحظة: نهاية f(x) عندما تقترب x من العدد c ليست بالضرورة تساوي f(c) فمثلا $\underset{x\to c}{\lim }f\left(x\right)=L$في الحالات الثلاث الآتية:

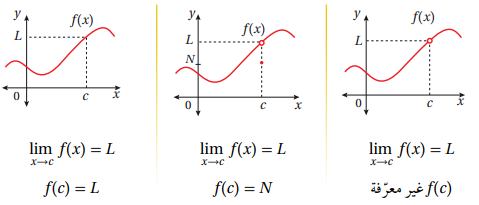
نهايات تتضمن المالانهاية:

إذا كانت النهاية من اليمين أو اليسار أو كليهما غير موجودة عند قيمة ما بسبب زيادة أو نقصان الاقتران بشكل غير محدود حول تلك القيمة، فإننا نصف سلوك الاقتران بأنه يقترب من المالانهاية الموجبة ($\infty$) أو السالبة ($-\infty$) حيث أن $\infty , -\infty$ ليسا عددين حقيقيين فقط هما يصفان سلوك الاقتران عند خط التقارب الرأسي.

 

إيجاد النهايات جبريا:

يتبع مجموعة من الخصائص التي تساعدنا على إيجاد النهايات جبريا

 

 

النهايات بالتعويض المباشر:

 

ملاحظة: إذا كان ناتج تعويض في النهاية يساوي $\frac{0}{0}$، فإننا نسمي هذه النتيجة الصيغة الغير المحددة وهي لا تعني أن النهاية غير موجودة ولكن نحن بحاجة إلى البحث عن صيغة مكافئ للاقتران من خلال تبسيطه جبريا إما بتحليل كل من البسط والمقام أو أنطاق البسط أو المقام واختصار العوامل المشتركة

 

الاتصال:

بيانيا: يكون الاقتران متصلا عند نقطة إذا لم يكن في تمثيله البياني أي انقطاع أو قفزة أو فجوة عند تلك النقطة.

جبريا: يكون الاقتران متصلا إذا حقق الشروط الآتية.