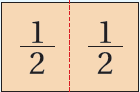
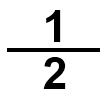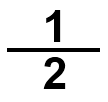النِّصْفُ
تهيئة
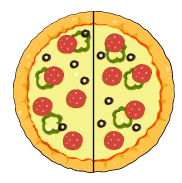
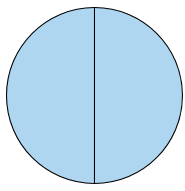
إذا أردنا أن نقسّم دائرة إلى جزأين متطابقين ، فإنّ كل جزء من الدائرة يُسمّى نِصْفًا، وللتوضيح أنظر إلى المثال الآتي:
يُسّمى هذا الشَّكل (دائِرَة)
أقوم بتقسيم الدائِرة إلى جزأين متطابقين، كما في الدرس السّابق (الأجزاء المُتطابقة)
والآن حصلنا على جزأين متطابقين، سنقوم بقصّ كل جزء من الأجزاء التي قمنا بتقسيمها
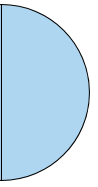
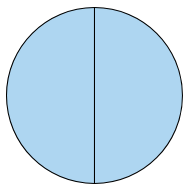
هذا الجزء الأول من الدائرة، ويمثّل نصف الدائِرة، لأنّ الجزء الآخر من الدائرة يُمثل النصف الثاني
هذا الشكل يمثل النّصف الثاني من الدائرة، وإذا أردنا أن نلصق نصفي الدائرة فإننا نحصل على (الكُل) = (الدائِرة).
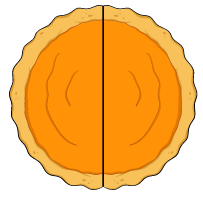
إِذا قَسَّمْتُ تُفاحَةً إِلى جُزْأَيْنِ مُتَطابِقَيْنِ، فَماذا أُسَمّي كُلَّ جُزْءٍ؟
أَتَأَمّلُ الشّكل الآتي:
- إنّ عدد الأجزاء المتطابقة التي سأحصل عليها عند تقسيم التّفاحة إلى جُزأَيْن هو (2)
- كل جزء بالنسبة إلى التفاحة يُمثِّل نصفًا.

إِذا قَسَّمْتُ الْكُلَّ إِلى جُزْأَيْنِ مُتَطابِقَيْنِ، فَإِنَّني أُسَمّي كُلَّ جُزْءٍ (النِّصْف) (one half)، وَأَكْتُبُهُ:
مثال:
إذا أردنا تقسيم المُستطيل الآتي إلى نصفين، فإنّ التقسيم يكون كما يأتي:
المُستطيل قبل أن أقوم بتقسيمه يُسمّى (الكُل).
أمّا إذا أردنا أن نقسّم المُستطيل إلى جزأين مُتطابقين فإنّ كل جزء منه يُسمّى نِصْفًا Fraction، ويُكتب بهذه الصورة:
أُلاحظ ذلك من خلال شكل المُستطيل بعد أن قمتُ بتقسيمه:
- إذا جمعنا النّصفين معًا، فإنني أحصل على (الكُل).
أستعين بالتوضيح الآتي:
النّصف يُمثّل جُزءًا مقسمومًا من الكُل، وهذا الجزء يكون مساويًا تمامًا للجزء الآخر الذي قسم من الكُل، أي (متطابق معه تمامًا) بحيث لو قمنا بقصّ الأجزاء ووضعناها فوق بعضها البعض لكانت متساوية تمامًا.
نَشاط:
أَتَأمّل الأشكال الآتية، ثُمَّ أَتَحَدّث كيف حصلنا على النّصف