رياضيات فصل ثاني

حلول أسئلة كتاب الطالب وكتاب التمارين

حل سؤال استكشف مقدمة الدرس

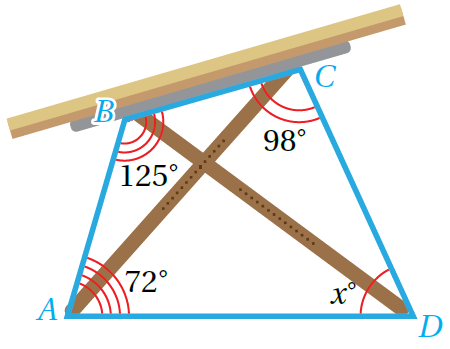
يظهرُ في الشكل المُجاور المُضلعُ الرباعي ABCD الذي تُشكلُهُ أرجُلُ طاولة رسمٍ. ما قيمةُ $x$ في الشكل؟ الجواب  الشكل الموضح باللون الأزرق رُباعي، إذن $x+98+125+72=360$ $x+295=360$ $x=360-295 \to x=65$

 

 

 

 

 

 

 

 

 

 

---

حلول أسئلة أتحقق من فهمي

أتحقق من فهمي صفحة 81

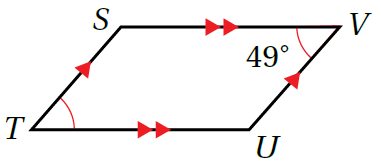
4) أُسمي الشكل المُجاور بأربع طرائق مُختلفةٍ. 5) أُسمي زوجًا من الأضلاع المُتوازية. 6) أجدُ قياس الزاوية $\angle \mathrm{STU}$

 

 

 

 

 

الجواب

4) 

الطّريقةُ (1) : أبدأُ بالرّأس S ، وأتحرّكُ باتّجاه عقارب السّاعة على النّحو الآتي: $\mathrm{S} \to V \to U \to \mathrm{T}$ إذن، أُسمّي الشّكل SVUT 

الطّريقةُ (2) : أبدأُ بالرّأس  S، وأتحرّكُ باتّجاه عكس عقارب السّاعة على النّحو الآتي: $\mathrm{S} \to T \to U \to \mathrm{V}$ إذن، أُسمّي الشّكل STUV 

الطّريقةُ (3): أبدأُ بالرّأس  V ، وأتحرّكُ باتّجاه عكس عقارب السّاعة على النّحو الآتي: $\mathrm{V} \to U \to T \to \mathrm{S}$ إذن، أُسمّي الشّكل VUTS 

الطّريقةُ (4): أبدأُ بالرّأس  V ، وأتحرّكُ باتّجاه عقارب السّاعة على النّحو الآتي: $\mathrm{V} \to S \to T \to U$ إذن، أُسمّي الشّكل VSTU 

 

5) الضّلعان $\overline{\mathrm{SV}}$ و $\overline{\mathrm{TU}}$ متوازيان   

 

6) $\angle \mathrm{STU}=\angle \mathrm{SVU}=49°$ (لأنّ كليهما يظهرُ داخلهُ قوس واحد)

---

أتحقق من فهمي صفحة 83

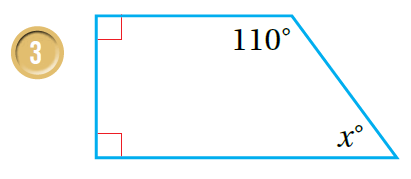
أجدُ قيمة $x$ في كُل من الشكال الرباعية الآتية:

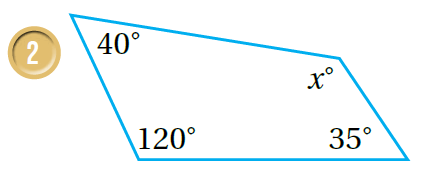مَجموعُ قِياساتِ زَوايا الشَّكْلِ الرُّباعِيِّ °360 ، إذن:	مَجموعُ قِياساتِ زَوايا الشَّكْلِ الرُّباعِيِّ °360 ، إذن:
$x+110+90+90=360$	$x+35+120+40=360$
$x+290=360$	$x+195=360$
$x=360-290 \to x=70$	$x=360-195 \to x=165$

---

أتحقق من فهمي صفحة 84

أجدُ قيمة $x$ في الشكال الآتية:

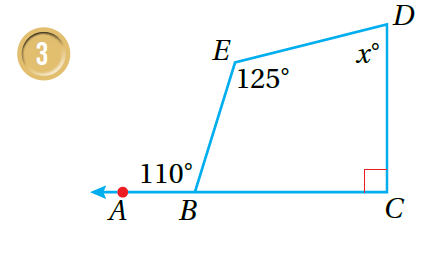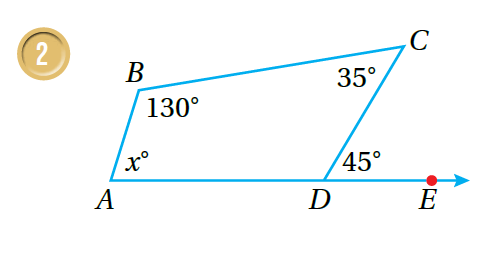مَجموعُ قِياساتِ الزَّوايا عَلى مُسْتَقيمٍ °180 ، إذن:	مَجموعُ قِياساتِ الزَّوايا عَلى مُسْتَقيمٍ °180 ، إذن:
$\mathrm{m}\angle \mathrm{EBC}+100=180$	$\mathrm{m}\angle \mathrm{EDC}+45=180$
$\mathrm{m}\angle \mathrm{EBC}=180-100 \to \mathrm{m}\angle \mathrm{EBC}=80°$	$\mathrm{m}\angle \mathrm{EBC}=180-45 \to \mathrm{m}\angle EBC=135°$
مَجموعُ قِياساتِ زَوايا الشَّكْلِ الرُّباعِيِّ °360 ، إذن:	مَجموعُ قِياساتِ زَوايا الشَّكْلِ الرُّباعِيِّ °360 ، إذن:
$x+80+125+90=360$	$x+135+130+35=360$
$x+295=360$	$x+300=360$
$x=360-295 \to x=65$	$x=360-300 \to x=60$

---

أتحقق من فهمي صفحة 85 أجدُ قيمتي $a$ و $b$ المجهولتين في الشكل المُجاور:                       الجواب الزاوبة $b$  هي زاوية داخل شكل رُباعي ، إذن: $b+40+40+140=360$
$b+220=360$
$b=360-220 \to b=140$
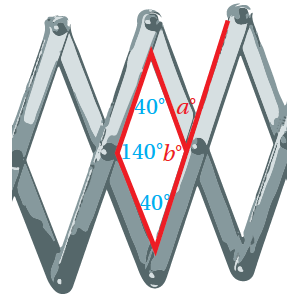الزاوية a هي زاوية خارج الشكل الرباعي ، وبما أن مَجْموعُ قِياساتِ الزَّوايا عَلى مُسْتَقيمٍ 180 ؛ إذن:
$a+b=180$
$a+140=180$
$a=180 - 140 \to a=40$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

حلول أسئلة أتدرب وأحل المسائل

أستعملُ الشكل المُجاور للإجابة عن الأسئلة الآتية:             1) أُسمي شكلين رُباعيين بطريقتين مُختلفتين 2) أُسمي ضلعين مُتوازيين. 3) أجدُ m∠BAD

 

 

 

 

 

 

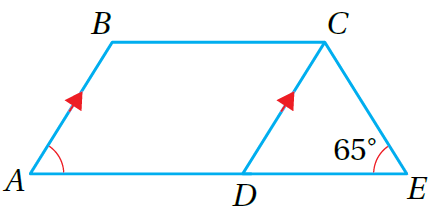الجواب

1) ABCD   ,   DABC

2) AB // DC

3) m∠BAD = m∠DEC  (أقواسُ مُتماثلةُ)

إذن: °m∠BAD = 65

---

أجدُ قيمة x في كُل مما يأتي:

$x+108+121+59=360$	$x+116+32+64=360$	$x+130+125+75=360$
$x+288=360$	$x+212=360$	$x+330=360$
$x=360-288=72$	$x=360-212=148$	$x=360-330=30$
$x+90+68+59=360$	$x+90+90+140=360$	$x+90+77+50=360$
$x+217=360$	$x+320=360$	$x+217=360$
$x=360-217=143$	$x=360-320=40$	$x=360-217=143$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

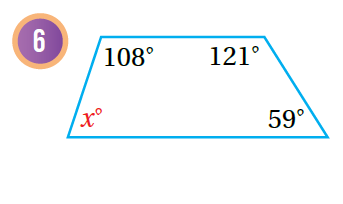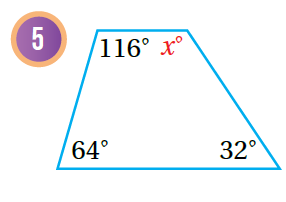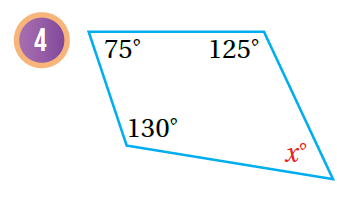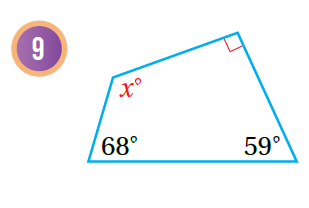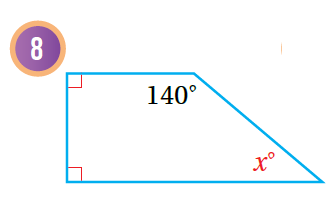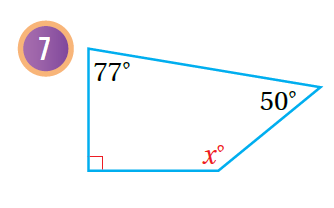أجدُ قيمة x, y في كُل مما يأتي:

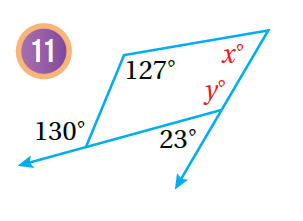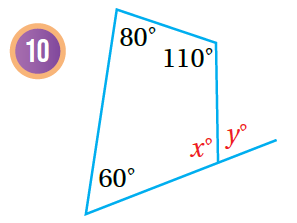مَجموعُ قِياساتِ الزَّوايا عَلى مُسْتَقيمٍ °180 ، إذن:	مَجموعُ قِياساتِ الزَّوايا عَلى مُسْتَقيمٍ °180 ، إذن:	مَجموعُ قِياساتِ زَوايا الشَّكْلِ الرُّباعِيِّ °360 ، إذن:
$x+100=180$	$y+23=180$	$x+110+80+60=360$
$x=180-100 \to x=80$	$y=180-23 \to y=157$	$x+250=360$
مَجموعُ قِياساتِ زَوايا الشَّكْلِ الرُّباعِيِّ °360 ، إذن:	ونحتاج إلى إيجاد قياس الزاوية المجاورة للزاوية 130 ، ولنرمز لها بالرمز (z) إذن:	$x=360-250 \to x=110$
$y+90+x+85=360$	$\mathrm{z}+130=180$	مَجموعُ قِياساتِ الزَّوايا عَلى مُسْتَقيمٍ °180 ، إذن:
$y+90+80+85=360$	$\mathrm{z}=180-130 \to \mathrm{z}=50$	$x+y=180$
$y+255=360$	مَجموعُ قِياساتِ زَوايا الشَّكْلِ الرُّباعِيِّ °360 ، إذن:	$110+y=180$
$y=360-255 \to y=105$	$x+y+\mathrm{z}+127=360$	$y=180-110 \to y=70$
	$x+157+50+127=360$
	$x+334=360$
	$x=360-334 \to x=26$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

13) رافعة: تُستخدمُ الرافعةُ المُبينةُ في الشكل المُجاور لرفع السيارات. أجدُ قيمة x        الجواب  الشكل الموضح باللون الأزرق رُباعي، إذن $x+80+80+100=360$ $x+260=360$ $x=360-260 \to x=100$

 

 

 

 

 

 

 

 

---

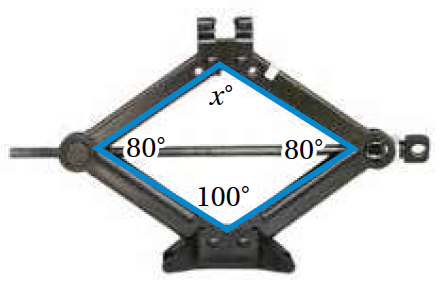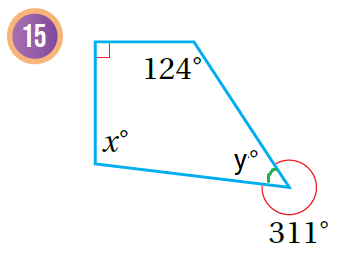
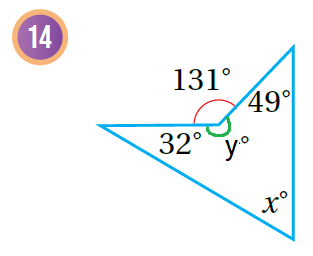
أجدُ قيمة x في كُل شكلٍ مما يأتي:

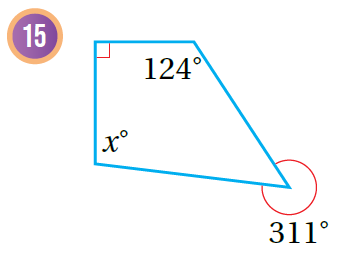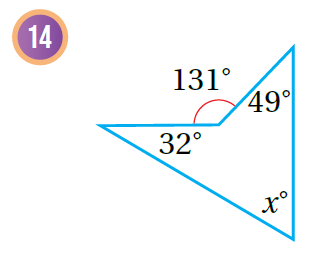تذكر أن مجموع الزوايا حول نقطة يساوي 360 ،	تذكر أن مجموع الزوايا حول نقطة يساوي 360 ،
إذن لنرمز للزاوية التي تشكل مع الزاوية 311 نقطة بالرمز (y)	إذن لنرمز للزاوية التي تشكل مع الزاوية 131 نقطة بالرمز (y)
$y+311=360$	$y+131=360$
$y=360-311 \to y=49$	$y=360-131 \to y=229$
مَجموعُ قِياساتِ زَوايا الشَّكْلِ الرُّباعِيِّ °360	مَجموعُ قِياساتِ زَوايا الشَّكْلِ الرُّباعِيِّ °360
$x+49+124+90=360$	$x+32+229+49=360$
$x+263=360$	$x+310=360$
$x=360-263 \to x=97$	$x=360-310 \to x=50$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

---

16) أجدُ قيمة كُل من a, b في الشكل المُجاور.

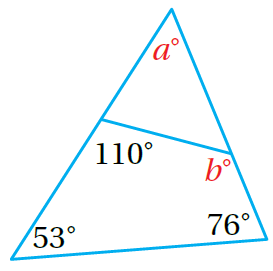
الجواب

مَجموعُ قِياساتِ زَوايا الشَّكْلِ الرُّباعِيِّ °360

$b+110+76+53=360$

$b+239=360$

$b=360-239 \to b=121$

مَجموعُ قياساتِ زوايا المُثلث °180 ، المثلث الكبير فيه:

$a+76+53=180$

$a+129=360$

$a=180-129 \to a=51$

 

حلول أسئلة مهارات التفكير العُليا

17) أكتشفُ الخطأ: سمى عامر الشكل الرباعي المُجاور TUSV . أكتشفُ خطأ عامرٍ، وأصُححُهُ.     الجواب الخطأ أن عامر ذكر اسم الشكل برؤوس غير متتالية. واسم الشكل الصحيح: TUVS

 

 

 

 

 

---

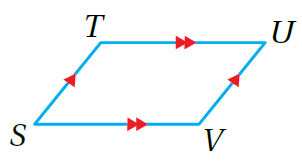18) تبرير: صممت حنانُ لوحةً للتوعية بخطر التدخين على شكل رُباعي كما في الشكل المُجاور. أجدُ قيمة الزاوية x المجهولة في اللوحة. 

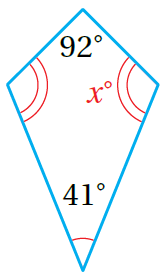
الجواب

تعني الأقواسُ المُتماثلةُ المرسومةُ داخل أيّ زاويتين أنّ لهُما القياس نفسهُ، فإذن يُمكن اعتبار أن الزاوية المقابلة هي (X) أيضا.

إذن، بما أن مجموع قياسات الشكل الرباعي 360 ، فإن:

$x+x+92+41=360$

$$\begin{gathered} 2x+133=360 \\ -133 -133 \end{gathered}$$

$2x=227$

$\frac{2}{2}x=\frac{227}{2}$

$x=113.5$

---

19) تحد: أجدُ قيم x, y, z في الشكل المُجاور. 

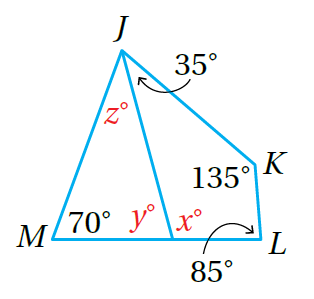
الجواب

مَجموعُ قِياساتِ زَوايا الشَّكْلِ الرُّباعِيِّ °360	$x+85+135+35=360$
	$x+255=360$
	$x=360-255$
	$x=105$
مَجموعُ قِياساتِ الزَّوايا عَلى مُسْتَقيمٍ °180	$y+x=180$
	$y+105=180$
	$y=180-105$
	$y=75$
مَجموعُ قياساتِ زوايا المُثلث °180	$z+y+70=180$
	$z+75+70=180$
	$z+145=180$
	$z=35$

---

20) أكتب: كيف يُمكنُ إيجادُ قياس زاويةٍ مجهولةٍ في شكلٍ رُباعي قياساتُ زواياهُ الثلاث الأخرى معلومة؟

الجواب

أجمع الزوايا المعلومة ثم أطرحها من  360 لأن مجموع زوايا الشكل الرباعي 360

---

حلول أسئلة كتاب التمارين

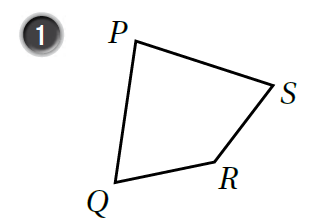
أُسَمّي كُلًّ منَ الشكال الرُّباعيَّة الآتيَة بطَريقَتَين:

$\mathrm{QONM} , \mathrm{MNOQ}$	$\mathrm{GFJH} , \mathrm{JHGF}$	$\mathrm{BCDA} , \mathrm{ABCD}$	$\mathrm{PSRQ} , \mathrm{RQPS}$

 

 

 

 

 

 

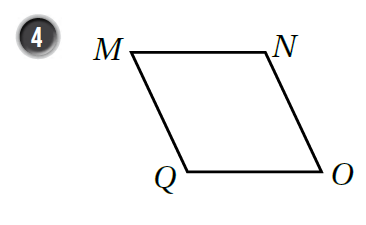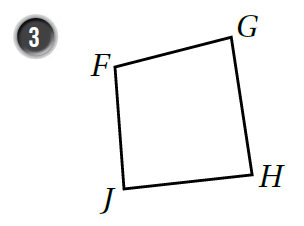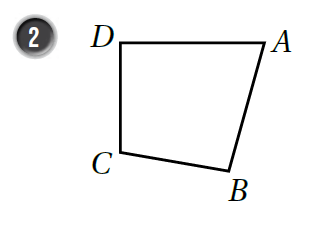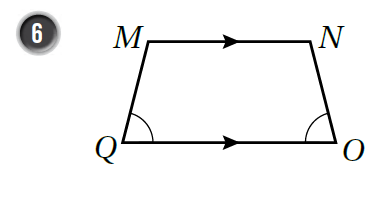
أُسَمّي زَوجًا منَ الأضلاع المُتَوازيَة، وَزَوجًا منَ الزَّوايا المُتَساويَة في كُلّ شَكلٍ رُباعيٍّ ممّا يَأتي:

$\overline{\mathrm{OL}} // \overline{\mathrm{NM}}$	$\overline{\mathrm{MN}}// \overline{\mathrm{QO}}$	$\overline{\mathrm{AB}} // \overline{\mathrm{DC}}$
$\mathrm{m}\angle \mathrm{OLM}=\mathrm{m}\angle \mathrm{LMN}$	$\mathrm{m}\angle \mathrm{MQO}=\mathrm{m}\angle \mathrm{NOQ}$	$\mathrm{m}\angle \mathrm{ABC}=\mathrm{m}\angle \mathrm{ADC}$

 

 

 

 

 

 

 

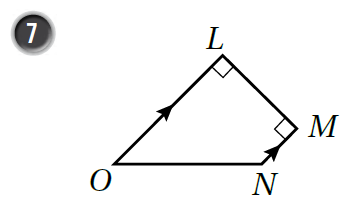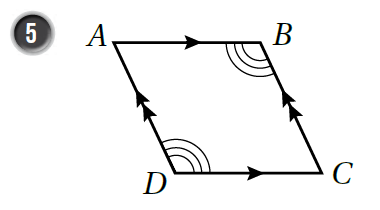أَجدُ قيمَةَ x في كُلّ شَكلٍ ممّا يَأتي:

$x= 114$	$x= 60$	$x= 60$

 

 

 

 

 

 

 

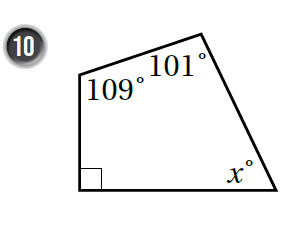11) أُبَيّنُ ما إذا كانَت الزَّوايا تُمَثّلُ زَوايا شَكلٍ رُباعيٍّ بوَضع إشارَة ( ✔) في العَمود المُناسب في الجَدوَل الآتي:

هَلِ الشَّكْلُ رُباعِيٌّ؟ِ		قِياساتُ زَوايا الشَّكْل
لا	نعم
✔		$24°, 47°, 120°, 200°$
	✔	$65°, 75°, 85°, 135°$
	✔	$120°, 115°, 77°, 48°$

 

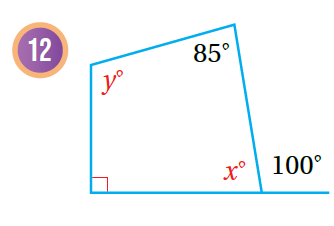
12) أَجدُ قيمَةَ كُلٍّ من x, y في الشَّكل المُجاور:

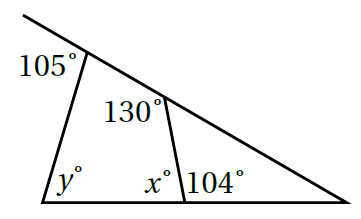$$\begin{gathered} 108-105={75}^{°} \\ y+x+130+75=360 \\ y+76+130+75=360 \\ y+281=360 \\ y=360-281 \\ y=79 \end{gathered}$$	$$\begin{gathered} x=108-104 \\ x=76 \end{gathered}$$