انكسار الضوء

 انكسارُ الضوء.

للضوءِ أهميّةٌ بالغةٌ في حياتِنا، وهو يحيطُ بنا

من كلِّ مكانٍ، فهوسببُ رؤيتِنا الأشياءَ من حولِنا،

ويُسهِّلُ علينا استكشافَ العالمِ المحيطِ بنا.

فلو أغمضْنا أعيُنَنا لحظةً، وتخيّلْنا عالمَ الظلامِ

الذي سنعيشُ فيهِ، فكيفَ سيبدو عالمُنا دونَ وجودِ الضوءِ؟

توجدُ  عملياتٌ مختلفةٌ تحدثُ وتساعدُنا على رؤيةِ العالمِ

من حولِنا، منها الانعكاسُ والانكسارُ، فالأجسامُ من

حولِنا تعكسُ الضوءَ الساقطَ عليها منَ المصادرِ الضوئيّةِ
المختلفةِ، كالشمسِ، والمصابيحِ، والأجسامِ المشتعلةِ،

وعندَما يدخلُ الضوءُ القادمُ من هذهِ الأجسامِ إلى أعيُنِنا

ينكسرُ عن طريقِ العدسةِ الموجودةِ في أعيُنِنا ويتركّزُ على

الشبكيّةِ، فتحدثُ الرؤيةُ.
وقد تعرّفْنا في صفٍّ سابقٍ الانعكاسَ، وسنتعرّفُ في هذا
الدرسِ خاصيّةً أخرى للضوءِ وهي الانكسارُ.

الانكسارُ Refraction
ينتقلُ الضوءُ في الفراغِ أو في الوسطِ الشفّافِ المتجانسِ
كالماءِ والزجاجِ بسرعةٍ ثابتةٍ وفي خطٍّ مستقيمٍ دونَ أن

ينحرفَ، ولكنْ هلْ يبقى كذلك عندَما ينتقلُ منَ الفراغِ إلى

وسطٍ شفّافٍ أو العكس، أو من وسطٍ شفّافٍ إلى وسطٍ

شفّافٍ آخرَ؟
عندما نضعُ قلمًا مائلًا في كأسٍ بها سائل، فإنَّ القلمَ

 يظهرُ مكسورًا عندَ سطحِ السائل على نحوِ ما يظهرُ

في الشكلِ ( 1)

وهذا يدلُّ على أنَّ الأشعّةَ الضوئيةَ القادمةَ منَ الجزءِ

 المغمورِ في الماءِ منَ القلمِ والساقطةَ على العينِ

قد غيّرتْ مسارَ حركتِها (انكسرتْ) عندما انتقلتْ منَ

الماءِ إلى الهواءِ، فما الذي أدّى إلى ظهورِ القلمِ

 مكسورًا؟ ولماذا تغيّرَ مسارُ الضوءِ عندما انتقلَ منَ

 الماءِ إلى الهواءِ؟
تبلغُ سرعةُ الضوءِ في الفراغِ ( c = 3 × 10⁸ m/s )

 تقريبًا، لكنَّها تقلُّ عن ذلكَ في الأوساطِ الشفّافةِ

 (كالهواءِ، والماءِ، والزجاجِ، ...)، وتختلفُ سرعةُ الضوءِ

في الأوساطِ الشفّافةِ باختلافِ هذهِ الأوساطِ، لذا عندما

ينتقلُ الضوءُ من وسطٍ شفّافٍ إلى وسطٍ شفّافٍ آخرَ

فإنَّ سرعتَه تتغيّرُ، ما يؤدّي إلى تغيّرِ مسارِه. ويُطلقُ على

ظاهرةِ تغيّرِ مسارِ الضوءِ عندَ انتقالِه بينَ وسطينِ شفّافينِ

مختلفينِ اسمَ: انكسارِ الضوءِ .Refraction of light

معاملُ الانكسارِ Refractive index
يُعرّفُ معاملُ الانكسارِ Refractive index للوسطِ

 الشفّافِ بأنَّه:
النسبةُ بينَ سرعةِ الضوءِ في الفراغِ ( c) إلى سرعتِه

 في الوسطِ الشفّافِ (ν) ويُرمزُ إلى معاملِ الانكسارِ

 بالرمزِ ( n)، أيْ أنَّ:

$n =\frac{\mathrm{سرعةَ} \mathrm{الضوءِ} \mathrm{في} \mathrm{الفراغِ}}{ \mathrm{سرعةِ} \mathrm{الضوءِ} \mathrm{في} \mathrm{الوسطِ} \mathrm{الشفافِ}}$  

     بالرموز  :         $n=\frac{c}{\nu }$

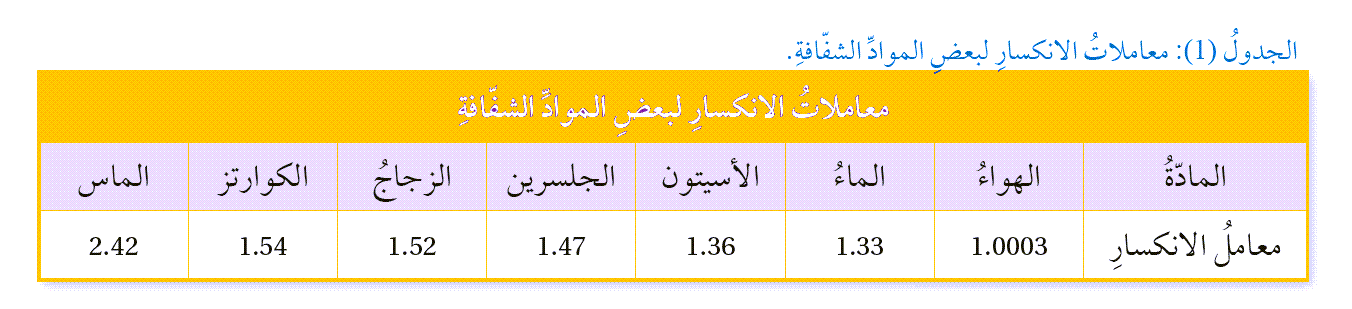
ونظرًا إلى أنَّ سرعةَ الضوءِ في الوسطِ الشفافِ

أقلُّ من سرعتِه في الفراغِ، فإنَّه وفقًا للمعادلةِ

السابقةِ تكونُ قيمةُ معاملِ الانكسارِ (n ≥ 1)،

حيثُ تساوي ( 1) للفراغِ، وهي أقلُّ قيمةٍ لمعاملِ

الانكسارِ.
ويُعدُّ معاملُ الانكسارِ مقياسًا لقدرةِ الوسطِ

الشفّافِ على كسرِ الأشعةِ الضوئيةِ، إذ كلَّما كانَ

معاملُ انكسارِ الوسطِ الشفافِ أكبرَ كانتْ قدرتُه

على كسرِ الأشعةِ الضوئيةِ أكبرَ، لكنَّ سرعتَه تقلُّ

معَ زيادةِ معاملِ الانكسارِ على نحوِ ما يظهرُ منَ

المعادلةِ السابقةِ، وألاحظُ أيضًا من المعادلةِ أنَّ

معاملَ الانكسارِ ليسَ لهُ وحدةُ قياسٍ، لأنَّه حاصلُ

قسمةِ كمّيتينِ لهما وحدةُ القياسِ نفسُها. ويُبيّنُ

الجدولُ ( 1) معاملاتِ الانكسارِ لبعضِ الموادِّ الشفّافةِ.

أُلاحظُ من الجدولِ أنَّ معاملَ الانكسارِ للهواءِ يساوي

( 1) تقريبًا، والذي يساوي معاملَ الانكسارِ للفراغِ.

مثال

بالاستعانةِ بالجدولِ ( 1)، أحسُبُ سرعةَ الضوءِ في الماءِ علمًا

 بأنَّ سرعتَه في الفراغِ 3x10⁸m/s

^الحل

^{بالتطبيقِ على معادلةِ حسابِ معاملِ الانكسارِ:}

^{$$\begin{gathered} n=\frac{c}{\nu } \\ 1.33=\frac{3\times {10}^8}{v} \\ v=\frac{3\times {10}^8}{1.33}=2.25 \times {10}^8 m/s \end{gathered}$$}

تمرين

الاستعانةِ بالجدولِ ( 1) أحسبُ سرعةَ الضوءِ في الزجاجِ:

  الحل:$$\begin{gathered} n=\frac{c}{\nu } \\ 1.52=\frac{3\times {10}^8}{v} \\ v=\frac{3\times {10}^8}{1.52} \end{gathered}$$

$=1.97 \times {10}^8 m/\mathrm{s \; \; \; }$

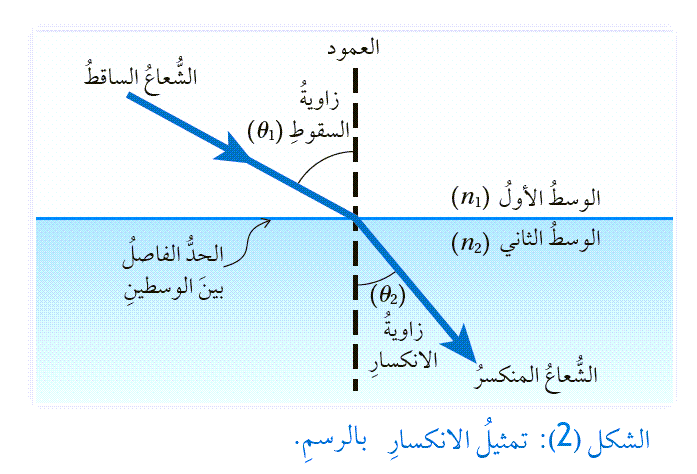
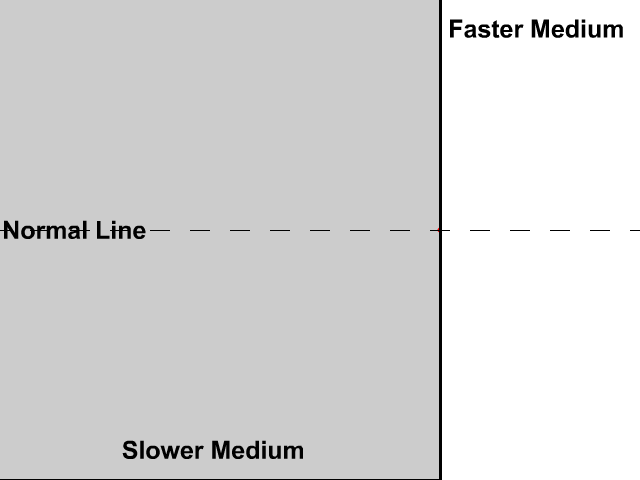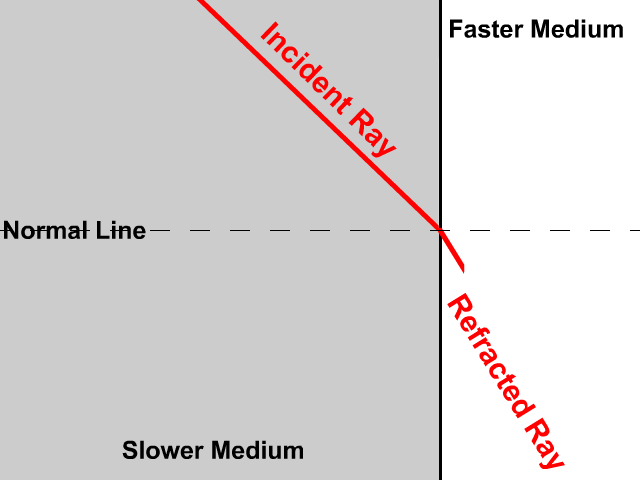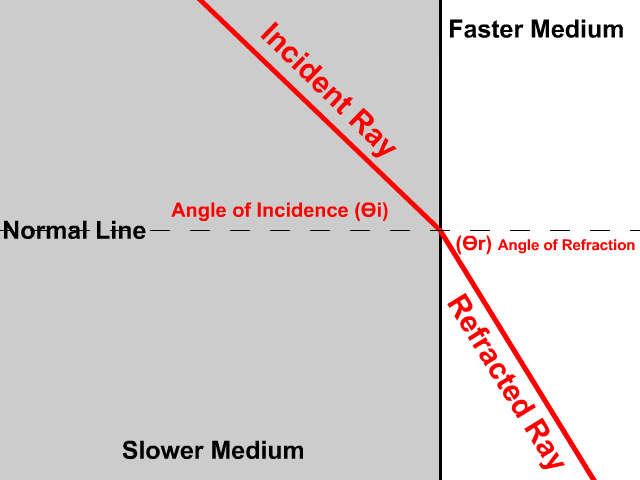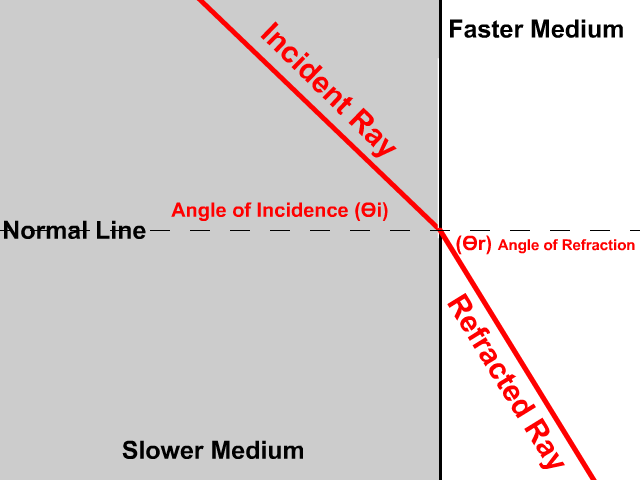
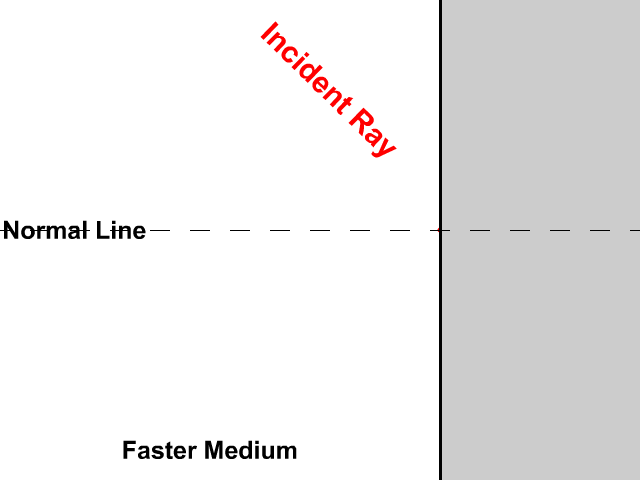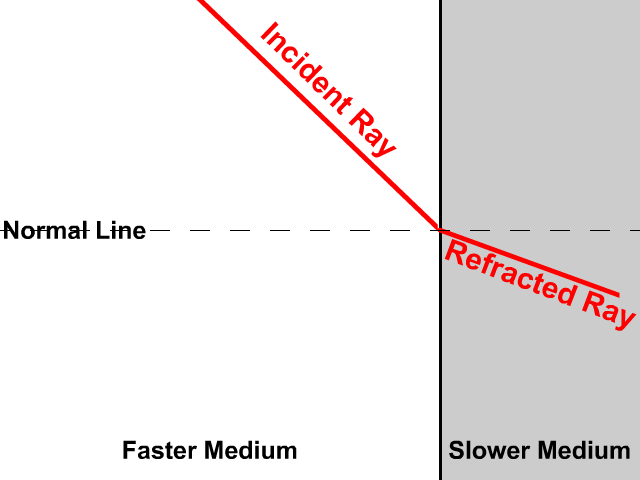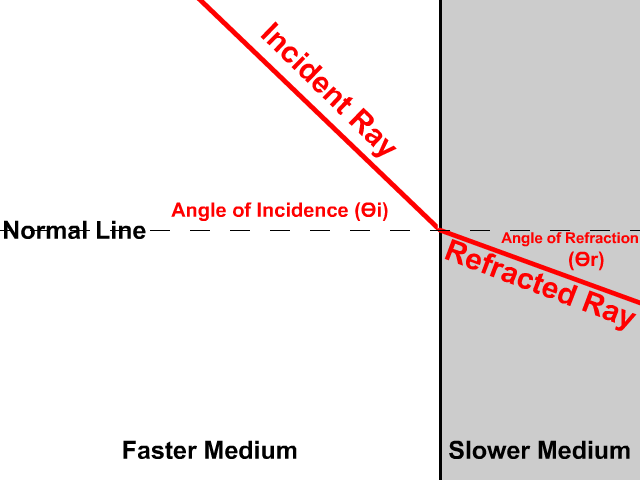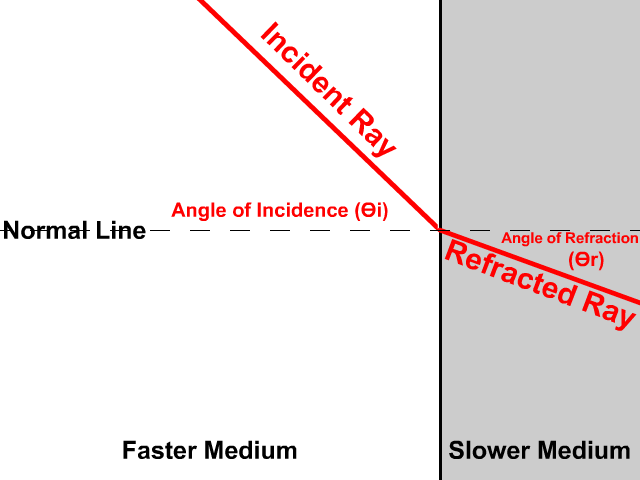
تمثيلُ الانكسارِ بالرسمِ

Representing Refraction with Diagrams
لفهمِ سلوكِ الضوءِ في أثناءِ انتقالِه في الأوساطِ الشفّافةِ،

يمكنُ تمثيلُ عمليةِ الانكسارِ برسومٍ تخطيطيّةٍ. فالشكلُ (2)

يمثّلُ انتقالَ شعاعٍ ضوئيٍّ بينَ وسطينِ شفّافينِ، وتُعرّفُ

المصطلحاتُ الواردةُ في الشكلِ على النحوِ الآتي:

الحدُّ الفاصلُ بينَ الوسطينِ: سطحُ التقاءِ الوسطِ الأولِ

  معَ الوسطِ الثاني.
العمودُ: الخطُّ العموديُّ على الحدِّ الفاصلِ بينَ الوسطينِ

 الشفّافينِ والمقامِ من نقطةِ السقوطِ (نقطةِ التقاءِ

الشعاعِ الساقطِ بالحدِّ الفاصلِ بينَ الوسطينِ).

زاويةُ السقوطِ Angle of incidence : الزاويةُ المحصورةُ

 بينَ الشعاعِ الساقطِ والعمودِ، ويُرمزُ إليها بالرمزِ.(θ₁)

زاويةُ الانكسارِ Angle of refraction :الزاويةُ المحصورةُ

 بينَ الشعاعِ المنكسرِ والعمودِ، ويُرمزُ إليها بالرمزِ.(θ₂)

وكلٌّ من الشعاعِ الساقطِ والشعاعِ المنكسرِ والعمودِ

 تقعُ جميعُها في مستوًى واحدٍ عموديٍّ على الحدِّ الفاصلِ

بينَ الوسطينِ.

مثال 

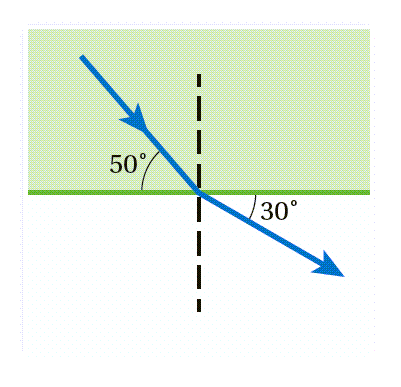
أُحدّدُ كلاً من زاويةِ السقوطِ وزاويةِ الانكسارِ في الشكلِ.

الحلُّ:
θ₁ : الزاويةُ التي يصنعُها الشعاعُ الساقطُ معَ العمودِ
˚θ₁ = 90˚ - 50˚ = 40
θ₂ : الزاويةُ التي يصنعُها الشعاعُ المنكسرُ معَ العمودِ
˚θ₂ = 90˚ - 30˚ = 60

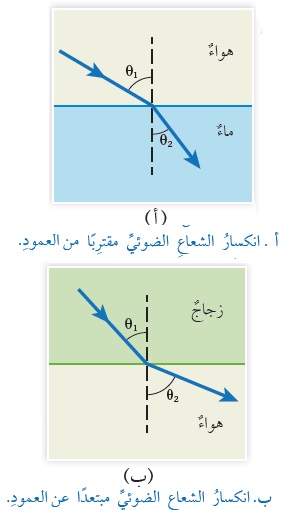
قانونُ الانكسارِ -قانونُ سنِل

The Law of Refraction (Snell’s Law)

عندما ينتقلُ شعاعٌ ضوئيٌّ من وسطٍ شفّافٍ معاملُ

انكسارِه صغيرٌ إلى وسطٍ شفّافٍ معاملُ انكسارِه

كبيرٌ فإنَّ سرعتَه تقلُّ، وينكسرُ مقترِبًا منَ العمودِ على

نحوِ ما هو مُبيَّنٌ في الشكلِ (3/أ)، وعندما ينتقلُ

الشعاعُ الضوئيُّ من وسطٍ شفّافٍ معاملُ انكسارِه

كبيرٌ إلى وسطٍ شفّافٍ معاملُ انكسارِه صغيرٌ فإنَّ

سرعتَه تزدادُ، وينكسرُ مبتعِدًا عن العمودِ على نحوِ

ما هو مبيَّنٌ في الشكلِ (3/ب). لكنْ ما العلاقةُ بينَ

زاويةِ السقوطِ ( θ₁ )وزاويةِ الانكسارِ (θ₂)؟

عامَ 1621 توصّلَ العالِمُ الألمانيُّ ويلبرورد سنِل 

(Willebrord Snell) تجريبيًّا إلى علاقةٍ رياضيّةٍ تربطُ

بينَ زاويتي السقوطِ والانكسارِ، وهي على الصورةِ

 الآتيةِ:
                n₁ sin θ₁ = n₂ sin θ₂
ويُطلقُ على العلاقةِ السابقةِ اسمَ قانونِ الانكسارِ أو

 قانونِ سنِل، حيثُ:
n₁ : معاملُ انكسارِ الوسطِ الأولِ
n₂ : معاملُ انكسارِ الوسطِ الثاني
θ₁ : زاويةُ السقوطِ
θ₂ : زاويةُ الانكسارِ

       شكل 3

مثال 

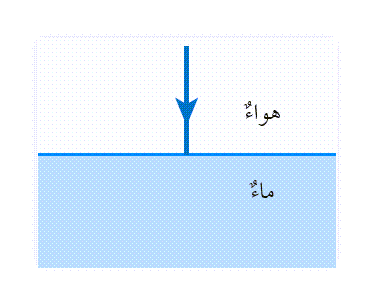
أحدّدُ الزاويةَ التي ينكسرُ فيها الشعاعُ الضوئيُّ في الشكلِ.

الحلُّ:

n₁ sin θ₁ = n₂ sin θ₂
1 × sin 0° = 1.33 × sin θ₂
θ₂ = 0°

وهذا يعني أنَّ الشعاعَ يستمرُّ في مسارِه دونَ انحرافٍ.

يتّضحُ منَ المثالِ السابقِ أنَّ الشعاعَ الضوئيَّ لا

يتغيّرُ مسارُه إذا سقطَ عموديًّا على السطحِ

الفاصلِ بينَ وسطينِ شفّافينِ، ومعَ ذلكَ فإنَّ

سرعتَه تتغيّرُ، فالانكسارُ هو نتيجةٌ لتغيُّرِ سرعةِ

الضوءِ عندَما ينتقلُ من وسطٍ شفّافٍ إلى وسطٍ

شفّافٍ آخرَ، وليس سببًا لهذا التغيّرِ.

مثال 

انتقلَ شعاعٌ ضوئيٌّ منَ الماءِ إلى وسطٍ شفّافٍ

 غيرِ معلومٍ، فإذا كانتْ زاويةُ سقوطِ الشعاعِ 45˚

وزاويةُ انكسارِه 38˚ ، فأحسبُ معاملَ انكسارِ

الوسطِ غيرِ المعلومِ، ثمَّ أحدّدُ طبيعتَه مستعينًا

بالجدولِ ( 1).

الحلُّ:

     n₁ sin θ₁ = n₂ sin θ₂
     sin 45° ×  1.33= n₂ × sin 38° 
       n₂ = 1.52
وبالرجوعِ إلى الجدولِ ( 1) يظهرُ أنَّ الوسطَ

الشفّافَ مصنوعٌ منَ الزجاجِ.

تمرين

انتقلَ شعاعٌ ضوئيٌّ منَ الماسِ إلى الماءِ، فإذا كانتْ زاويةُ

  سقوطِ الشعاعِ ° 30 ، فأحسبُ ما يأتي:
1 . سرعةُ الضوءِ في الماسِ.

2 . زاويةُ انكسارِ الشعاعِ في الماءِ.

      الحل:أ.

      $$\begin{gathered} n=\frac{c}{\nu } \\ 2.42=\frac{3\times {10}^8}{v} \\ v=\frac{3\times {10}^8}{2.42}=1.24 \times {10}^8 m/s \end{gathered}$$

    ب. n₁ sin θ₁ = n₂ sin θ₂
          2.42Xsin30^o=1.33xsinθ₂

            2.42x0.5=1.33sinθ₂

                       65^o =  sin^-1(0.91)= θ₂