مدرسة جواكاديمي

هنا يمكنك تصفح مدرسة جو اكاديمي، المنهاج، اسئلة، شروحات، والكثير أيضاً

تشابه المثلثات

رياضيات - الصف الثامن

فهرس الكتاب

الشرح

النتاجات

الملخص

أوراق العمل

حل اسئلة الدرس

تشابه المثلثات

المضلعات المتشابهة هي مضلعات زواياها المتناظرة متطابقة ، وأطوال أضلاعها المتناظرة متناسبة ، وتعد المثلثات هي حالة خاصة من المضلعات ،

وتوجد مسلمات ونظريات لإثبات تشابه المثلثات .

...............................................................................................................................................................................................................................................................................

مسلمة:

إذا طابقت زاويتان في مثلث زاويتين في مثلث آخر، فإن المثلثين متشابهان. (AA)

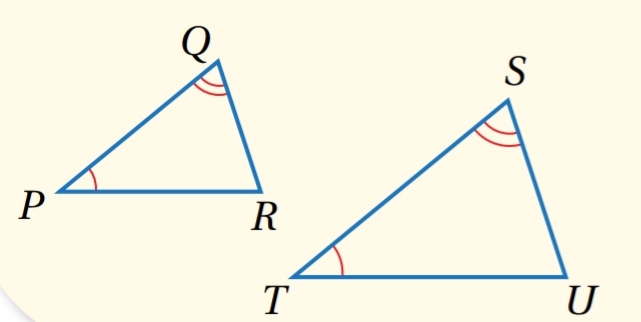
مثال : إذا كانت $∠ Q ≅ ∠ S, ∠ P ≅ ∠ T$ ، فإن $△ P Q R ~ △ T S U$

مثال ( 1 ) :

أحدد ما إذا كان كل مثلثين مما يأتي متشابهين أم لا ، وإذا كانا كذلك ، فأكتب عبارة التشابه ، مبرراً إجابتي.

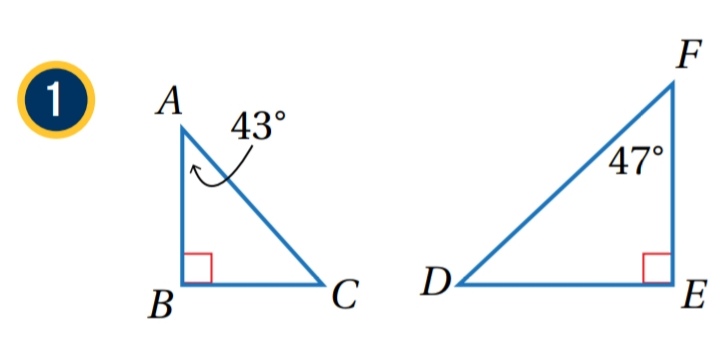
$∠ B ≅ ∠ E$ ، لأنهما زاويتان قائمتان

باستعمال مجموع قياسات زوايا المثلث يكون :

$m ∠ C = 180 ° - (90 ° + 43 °) = 47 ° m ∠ C ≅ ∠ F فإن m ∠ F = 47 ° أن بما$

إذن : $△ A B C ~ △ D E F$ ، وفق المسلمة ( AA)

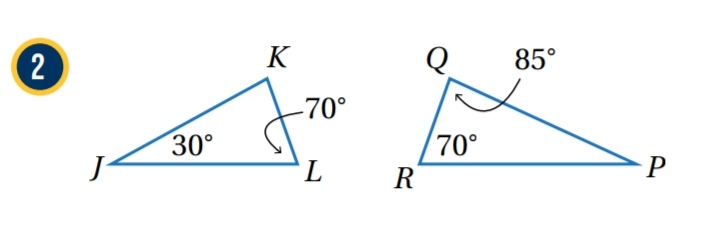
$∠ L ≅ ∠ R$ ، لأن كلا الزاويتين قياسهما 70

باستعمال مجموع قياسات زوايا المثلث يكون

$m ∠ K = 180 ° - (30 ° + 70 °) = 80 ° m ∠ P = 180 ° - (85 ° + 70 °) = 25 °$

وبما أنه يوجد زوج واحد فقط من الزوايا المتطابقة ، إذن $△ P Q R, △ J K L$ ليسا متشابهين .

نظريات:

- التشابه بثلاثة أضلاع ( SSS )

إذا كانت الأضلاع المتناظرةلمثلثين متناسبة، فإن المثلثين متشابهان.

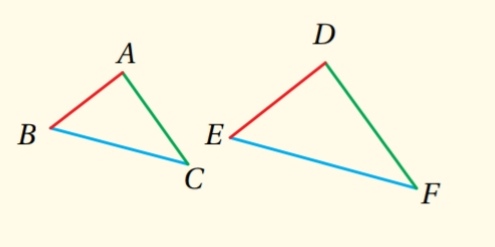
مثال: إذا كان $\frac{A B}{D E} = \frac{A C}{D F} = \frac{E F}{B C}$ ، فإن $△ A B C ~ △ D E F$

- التشابه بضلعين وزاوية محصورة ( SAS )

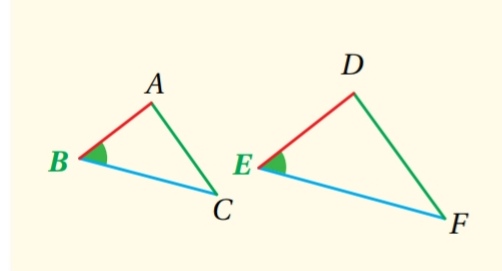
إذا كان طولا ضلعين في مثلث متناسبين مع طولي الضلعين المناظرين لهما في مثلث آخر ، وكانت الزاويتان المحصورتان بينهما متطابقتين ، فإن المثلثين متشابهان.

مثال: إذا كان $∠ B ≅ ∠ E, \frac{A B}{D E} = \frac{B C}{E F}$ ، فإن $△ A B C ~ △ D E F$

مثال ( 2 ) : أحدد ما إذا كان كل مثلثين مما يأتي متشابهين أم لا، وإذا كانا كذلك ، فأكتب عبارة التشابه ، مبرراً إجابتي،

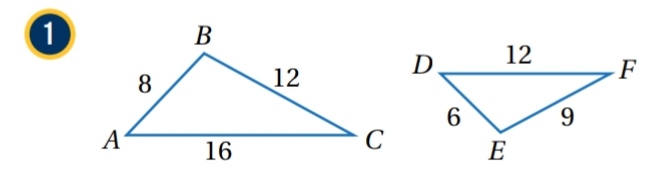
أستعمل أطوال الأضلاع لتمييز الأضلاع المتقابلة ، ثم أجد النسبة بين طول كل زوج من أزواج الأضلاع المتقابلة في المثلثين

أقصر ضلعين :

$\frac{A B}{D E} = \frac{8}{6} = \frac{4}{3}$

أطول ضلعين :

$\frac{CA}{FD} = \frac{16}{12} = \frac{4}{3}$

الضلعان المتبقيان :

$\frac{BC}{EF} = \frac{12}{9} = \frac{4}{3}$

بما أن النسب جميعها متساوية ، إذن $△ A B C ~ △ D E F$ وفق نظرية التشابه ( SSS )

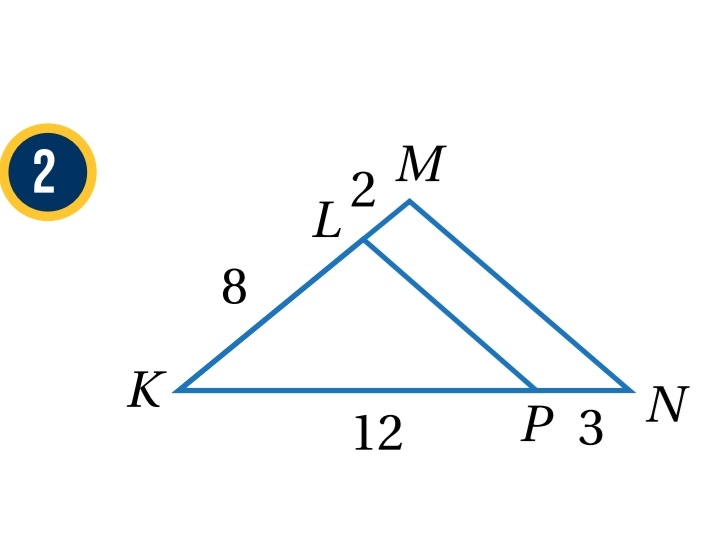
بما أن $∠ K$ مشتركة بين المثلثين ، إذن أجد النسبة بين طولي زوجي الأضلاع المتقابلة اللذين يحصران $∠ K$ في المثلثين

أقصر ضلعين :

$\frac{K L}{K M} = \frac{8}{10} = \frac{4}{5}$

أطول ضلعين :

$\frac{K P}{KN} = \frac{12}{15} = \frac{4}{5}$

بما أن طولي الضلعين اللذين يحصران $∠ K$ في $△ K L P$ متناسبان مع طولي الضلعين المناظرين لهما في $△ K M N$ ، إذن $△ K L P ~ △ K M N$ وفق نظرية التشابه ( SAS )

مثال ( 3 ) : أستعمل المعلومات المعطاة في الشكل المجاور ، لأثبت أن $△ S V R ~ △ U V T$ باستعمال البرهان ذي العمودين :

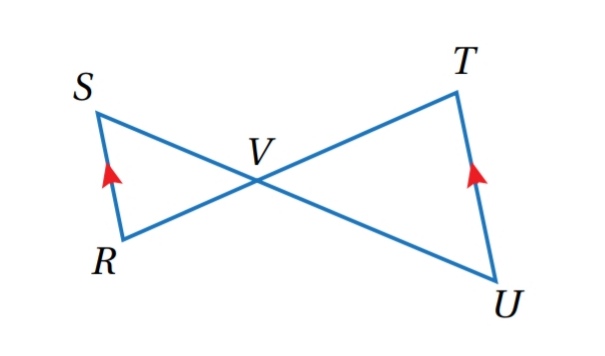
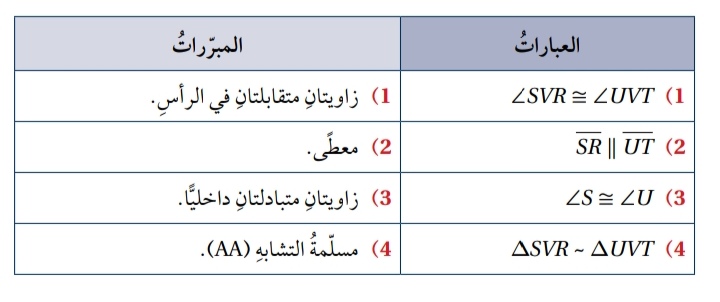
مثال ( 4 ) : أجد قيمة x التي تجعل أطوال الأضلاع المتناظرة متناسبة :

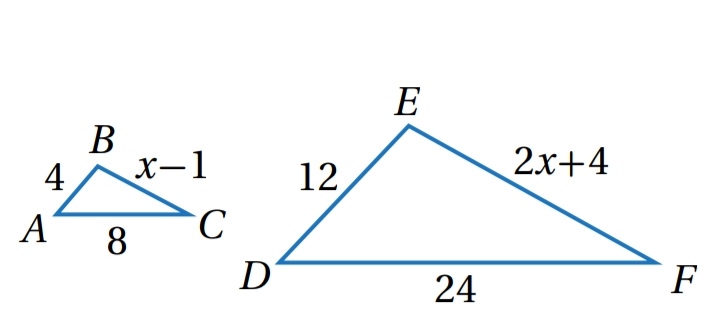
$\frac{A B}{D E} = \frac{B C}{E F} التناسب أكتب \frac{4}{12} = \frac{x - 1}{2 x + 4} أعوض 4 (2 x + 4) = 12 (x - 1) التبادلي بالضرب 8 x + 16 = 12 x - 12 التوزيع خاصية - 4 x + 16 = - 12 المعادلة طرفي من 12 x أطرح - 4 x = - 28 المعادلة طرفي من 16 أطرح x = 7 - 4 على المعادلة طرفي أقسم$

مسألة حياتية :

يريد مساح قياس عرض بحيرة باستعمال تقنية المسح المبينة في الشكل المجاور ، أجد عرض البحيرة ( VW )

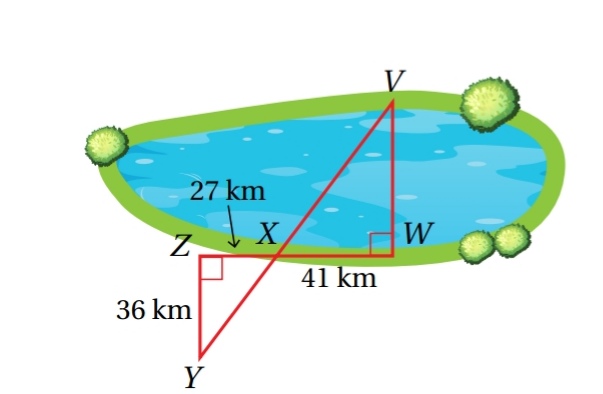
الحل :

أثبت أن $△ Y Z X ~ △ V W X$

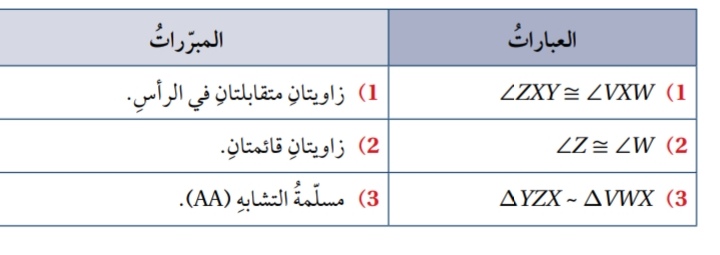
بما أن $△ Y Z X ~ △ V W X$ فيمكن استعمال التناسب بين أطوال الأضلاع المتناظرة لإيجاد عرض البحيرة.

أفترض أن VW= x

$\frac{Y Z}{V W} = \frac{Z X}{W X} التناسب أكتب \frac{36}{x} = \frac{27}{41} أعوض 27 x = 1476 التبادلي بالضرب x \approx 54.7$

إذن عرض البحيرة يساوي 54.7km تقريباً

مدرسة جواكاديمي

تشابه المثلثات

رياضيات - الصف الثامن

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS