الدرس الأول : تكاملات اقترانات خاصة
صيغ تكاملات اقترانات أسية :
أتحقق من فهمي صفحة 10 :
أجد كلاّ من التكاملات الآتية :
صيغ تكاملات اقترانات مثلثية:
أتحقق من فهمي صفحة 12 :
أجد كلاّ من التكاملات الآتية :
المتطابقات المثلثية والتكامل :
أتحقق من فهمي صفحة 14:
أجد كلاّ من التكاملات الآتية :
تكاملات ينتج منها اقتران لوغرتمي :
أتحقق من فهمي صفحة 16:
أجد كلاّ من التكاملات الآتية :
أتحقق من فهمي صفحة 17:
أجد :
تكامل الاقترانات المتشعبة :
أتحقق من فهمي صفحة 19:
إذا كان ، فأجد قيمة :
إذا كان ، فأجد قيمة :
إذا كان ، فأجد قيمة :
تطبيقات التكامل الشرط الأوَّلي :
أتحقق من فهمي صفحة 20:
تلوّث: تسرَّب نفط من ناقلة بحرية مكوناً بقعة دائرية الشكل على سطح الماء .نصف قطرها قدماً
بعد ثانية من بدء التسرُّب . إذا كان نصف قطر الدائرة يزداد بمعدَّل .
فأجد علماً .
تطبيقات التكامل الحركة في مسارٍ مستقيم:
أتحقق من فهمي صفحة 23:
يتحرك جسيم في مسارٍ مستقيم وتعطى سرعته المتجهة بالاقتران .
حيث الزمن بالثواني ، السرعة المتجهة بالمتر لكل ثانية .
إذا بدء الجسيم حركته من نقطة الأصل ، فأجد موقع الجسم بعد ثانية من بدء الحركة .
أجد إزاحة الجسيم في الفترة .
أجد المسافة الكلية التي قطعها الجسيم في الفترة .
تمارين ومسائل صفحة 26 :
أجد كلاّ من التكاملات الآتية :
إذا كان ، فأجد قيمة :
أجد مساحة المنطقة المظللة بين المحور x ومنحنى الاقتران : 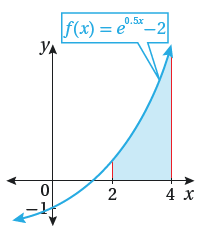
الممثل في الشكل المجاور .
إذا كان فأجد قيمة الثابت a ، حيث a > 0 .
أثبت أن : ، حيث
يبيّن الشكل المجاور منحنى الاقتران : . إذا كانت مساحة المنطقة
المحصورة بين منحنى الاقتران f(x) ، والمحور x ، والمستقيمين : x =1 ، x = a 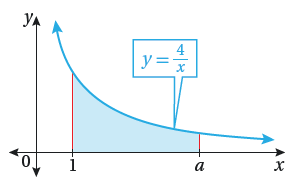
هي 10 وحدات مربعة ، فأجد قيمة الثابت a .
إذا كان ، وكان ، فأجد f(0) .
إذا كان ، وكان : y =1 عندما ،
فأثبت أنه يمكن كتابة y في صورة
يمثل الاقتران ميل المماس لمنحنى الاقتران y .
أجد قاعدة الاقتران y إذا علمت أن منحناه يمر بالنقطة (0 , 1) .
إذا كان ، فأجد قيمة الثابتين النسبيين:a ، b.
يمثل الاقتران ميل المماس لمنحنى الاقتران f(x) .
أجد قاعدة الاقتران f إذا علمت أن منحناه يمر بنقطة الاصل .
يتحرك جسيم في خط مستقيم ، وتعطى سرعته المتجهة بالاقتران : ، حيث t الزمن بالثواني ،
وv سرعته المتجهة بالمتر لكل ثانية . إذا كان الموقع الابتدائي للجسيم هو 3m ، فأجد كلاًّ مما يأتي:
موقع الجسيم بعد t ثانية .
موقع الجسيم بعد 100 ثانية
بيئة : في دراسة تناولت أحد أنواع الحيوانات المهددة بالانقراض في غابة ، تبيّن أن عدد حيوانات هذا النوع P(t)
يتغير بمعدل : P'(t) = - 0.51 e-0.03t ، حيث t الزمن بالسنوات بعد بدء الدراسة :
أجد قاعدة الاقتران P(t) عند أي زمن t ، علماً بإن عدد حيوانات هذا النوع عند بدء الدراسة هو 500 حيوان .
أجد عدد الحيوانات بعد 10 سنوات من بدء الدراسة ، مقرباً إجابتي لأقرب عدد صحيح
طب: في تجربة لدواء جديد أعطي لمريض لديه مرض حميد ، حجم 30cm3 . تبيّن أن حجم الورم بعدt يوماً
من بدء التجربة يتغير بمعدل P'(t) =0.15 – 0.9e0.006t مقيساً بوحدة cm3/day
أجد قاعدة حجم الورم بعد t يوما من بدء التجربة .
أجد حجم الورم بعد 10 أيام من بدء التجربة .
تبرير: أجد مساحة المنطقة المظللة في كل من التمثيلين البيانيين الآتيين ، مبرراً إجابتي .
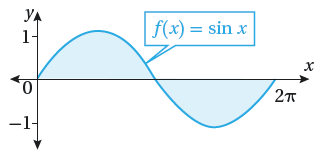
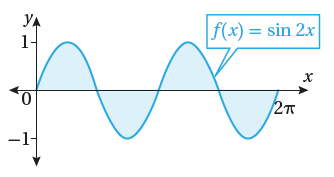
أجد كلاّ من التكاملات الآتية :
تبرير : إذا كان فأجد قيمة الثابت a ، حيث a > 0
تبرير : اثبت بطريقتين مختلفتين أن
تبرير : إذا كان فأجد قيمة الثابت k ، مبرراً اجابتي .
تحد: يتحرك جسيم في خط مستقيم ، وتعطى سرعته المتجهة بالاقتران : ،
حيث t الزمن بالثواني ، و v سرعته المتجهة بالمتر لكل ثانية . إذا بدأ الجسيم حركته من نقطة الأصل ،
فأجد كلاًّ مما يأتي:
موقع الجسيم بعد 5 ثواني من بدء الحركة .
موقع الجسيم بعد 9 ثواني من بدء الحركة .
تحد: يبيّن الشكل المجاور المنطقة المحصورة بين منحنى الاقتران : . 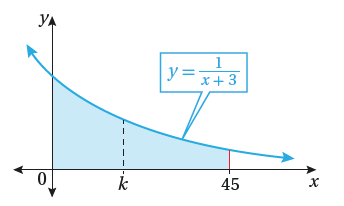
والمحور x ، والمستقيمين :x = 45 ، x = 0 .
أجد قيمة الثابت k التي تقسم المنطقة المظللة إلى منطقتين متساويتين .




