تمييز متوازي الأضلاع - الشرح - الصف الثامن - رياضيات فصل ثاني - مدرسة جواكاديمي

تمييز متوازي الأضلاع

شروط متوازي الأضلاع :

عكس نظرية الأضلاع المتقابلة في متوازي الأضلاع:

إذا كان كل ضلعين متقابلين متطابقين في الشكل الرباعي ، فإن الشكل الرباعي متوازي أضلاع.

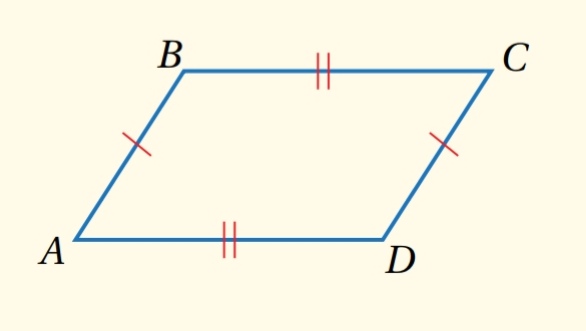
مثال : إذا كان $A B ≅ D C, B C ≅ A D$ ، فإن ABCD متوازي أضلاع .

.........................................................................................................................................................................................................................................................................................................

عكس نظرية الزوايا المتقابلة في متوازي الأضلاع:

إذا كانت كل زاويتين متقابلتين متطابقتان في الشكل الرباعي ، فإن الشكل الرباعي متوازي أضلاع .

مثال : إذا كان $∠ A ≅ ∠ C, ∠ B ≅ ∠ D$ فإن الشكل الرباعي ABCD متوازي أضلاع

مثال ( 1 ) : برهان نظرية :

في الشكل المجاور ، إذا كان $B C ≅ A D, A B ≅ C D$ فأثبت أن ABCD متوازي أضلاع باستعمال البرهان ذي العمودين :

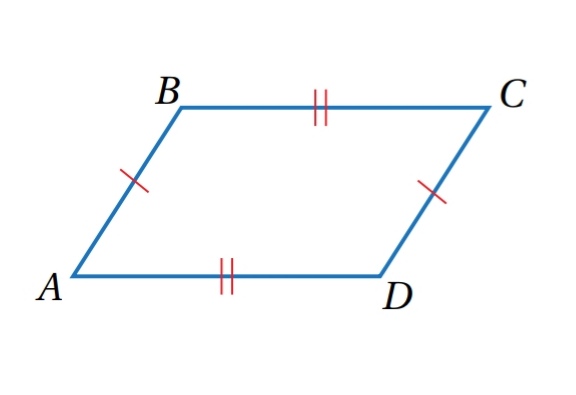
الحل :

أخطط للبرهان باستعمال الخطوات الاتية :

1- أرسم القطر AC ، لينتج $△ C D A, △ A B C$

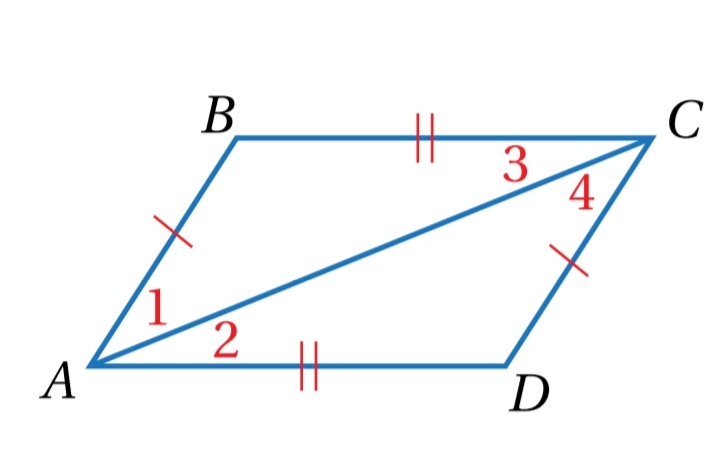
2- أستعمل حالة تطابق مثلثين بثلاثة أضلاع ( SSS ) ، لأثبت أن $△ A B C ≅ △ C D A$

3- أستعمل الزوايا المتبادلة داخلياً ، لأثبت أن الاضلاع المتقابلة متوازية .

البرهان :

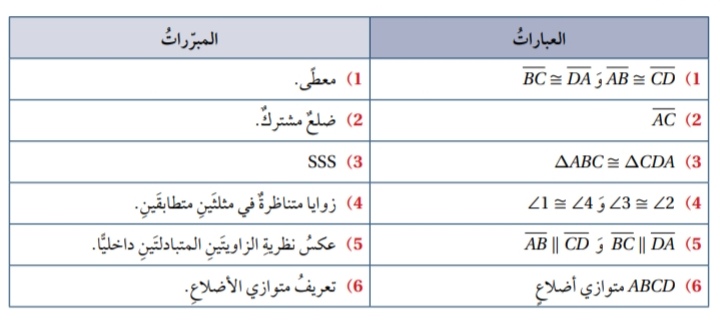
مثال ( 2 ) : مسألة حياتية :

يبين الشكل المجاور رافعة للمركبات الثقيلة :

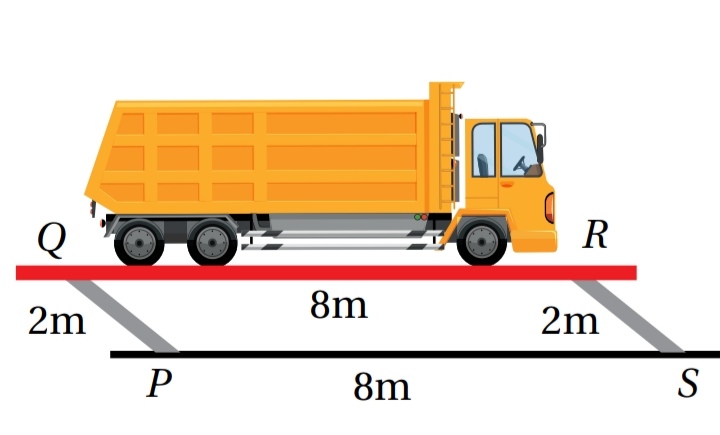
( 1 ) : هل الشكل الرباعي QRSP متوازي أضلاع ؟ أبرر إجابتي .

الحل :

بما أن كل ضلعين متقابلين في الشكل الرباعي QRSP متطابقان ، فإنه متوازي أضلاع .

( 2 ) : هل الشاحنة موازية للأرض ؟ أبرر إجابتي .

الحل :

بما أن QRSP متوازي أضلاع ، فإن $Q R ∥ P S$ ، وبما أن QR يمثل المنصة التي تستقر عليها الشاحنة ، و PS يقع على الأرض ، فإن الشاحنة موازية للأرض.

شروط متوازي الأضلاع :

عكس نظرية قطري متوازي الأضلاع :

إذا كان قطرا شكل رباعي ينصف كل منهما الاخر ، فإن الشكل الرباعي متوازي أضلاع .

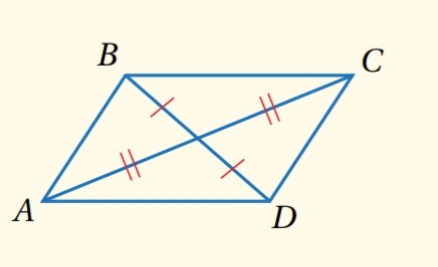
مثال : إذا كان AC و BD ينصف كل منهما الآخر، فإن ABCD متوازي أضلاع .

نظرية الأضلاع المتوازية والمتطابقة :

إذا توازى وتطابق ضلعان متقابلان في شكل رباعي ، فإن الشكل الرباعي متوازي أضلاع .

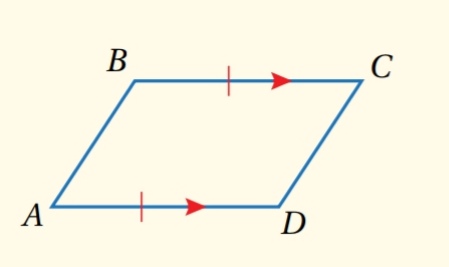
مثال: إذا كان $B C ∥ A D$ و $B C ≅ A D$ فإن ABCD متوازي أضلاع .

مثال ( 3 ) :

أجد قيمة x التي تجعل الشكل الرباعي FCDE المجاور متوازي أضلاع :

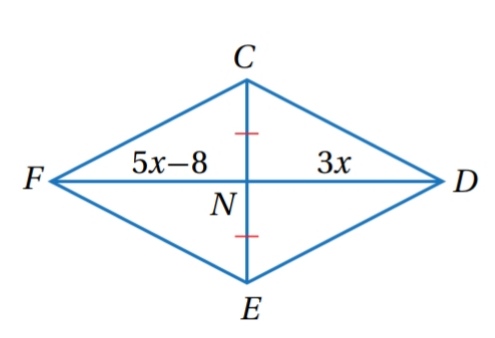
الحل:

بناءً على عكس نظرية قطري متوازي الأضلاع ، فإنه إذا كان قطرا شكل رباعي ينصف كل منهما الآخر ،

فإن الشكل الرباعي متوازي أضلاع ،

وبما أنه معطى في الشكل أن $C N ≅ E N$ ، أجد قيمة x التي تجعل $F N ≅ D N$

$F N = D N 5 x - 8 = 3 x 2 x - 8 - 3 x = 3 x - 3 x 2 x - 8 = 0 2 x - 8 + 8 = 0 + 8 2 x = 8 \frac{2 x}{2} = \frac{8}{2} x = 4$

عندما x = 4 ، فإن :

$F N = 5 (4) - 8 F N = 12 D N = 3 (4) D N = 12$

إذن ، عندما تكون x = 4 ، يكون الشكل الرباعي FCDE متوازي أضلاع .

طرائق إثبات أن الشكل الرباعي متوازي أضلاع :

يكون الشكل الرباعي متوازي أضلاع إذا حقق أياً من الشروط الآتية :

1- إذا كان كل ضلعين متقابلين فيه متوازيين

2- إذا كان كل ضلعين متقابلين فيه متطابقين

3- إذا كانت كل زاويتين متقابلتين فيه متطابقتين

4- إذا كان قطراه ينصف كل منهما الآخر

5- إذا كان فيه ضلعان متقابلان متوازيان ومتطابقان

مثال ( 4 ) :

أثبت أن $A (2, - 1), B (1, 3), C (6, 5), D (7, 1)$ تمثل رؤوس متوازي أضلاع :

الحل :

يمكن إثبات أن الأضلاع المتقابلة متوازية إذا كان لها الميل نفسه

(1 ) أمثل الشكل الرباعي في المستوى الاحداثي

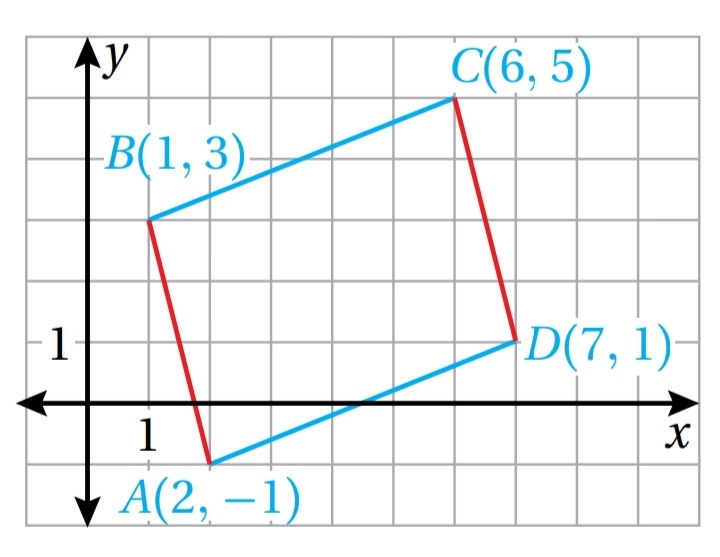
( 2) أجد ميل كل ضلع من أضلاع الشكل الرباعي

$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} الميل صيغة m = \frac{3 - (- 1)}{1 - 2} = - 4 A B ميل m = \frac{1 - 5}{7 - 6} = - 4 C D ميل m = \frac{5 - 3}{6 - 1} = \frac{2}{5} B C ميل m = \frac{- 1 - 1}{2 - 7} = \frac{- 2}{- 5} = \frac{2}{5} D A ميل$

بما أن الضلعين المتقابلين AB و CD لهما الميل نفسه ، إذن فهما متوازيان ، وبما أن الضلعين المتقابلين DA و BS لهما الميل نفسه ، إذن فهما متوازيان،

وبما أن الأضلاع المتقابلة متوازية ، إذن فالشكل الرباعي ABCD متوازي أضلاع .

رياضيات فصل ثاني

الثامن

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS