تمييز متوازي الأضلاع
حل اسئلة أتحقق من فهمي :
أتحقق من فهمي :
في الشكل المجاور إذا كان ، فأثبت أن ABCD متوازي أضلاع .
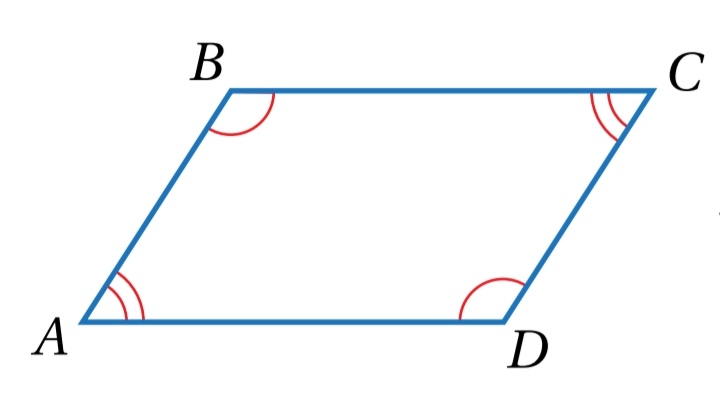
نرسم القطر CA
.................................................................................................................................................................................................................................................................
أتحقق من فهمي :
ما أقصى ارتفاع يمكن أن ترفع الرافعة الشاحنه إليه ؟ أبرر إجابتي.
الحل :
عندما يكون يكون أقصى ارتفاع يمكن أن ترفع الرافعة الشاحنه اليه هو 2m
.................................................................................................................................................................................................................................................................
أتحقق من فهمي :
أجد قيمتي x و y اللتين تجعلان الشكل الرباعي PQRS المجاور متوازي أضلاع.
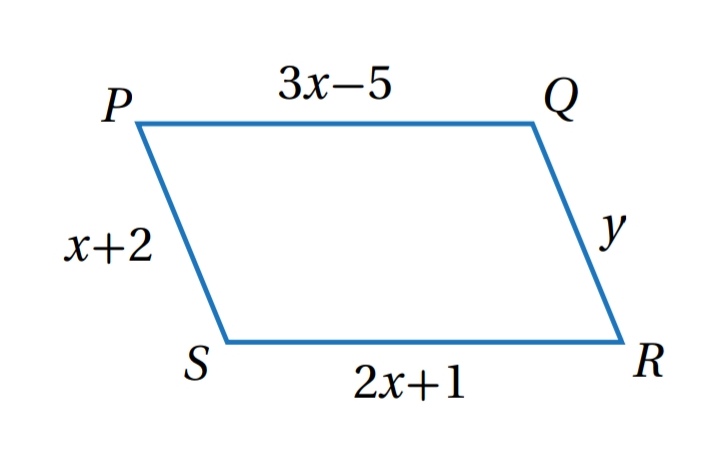
الحل :
بناءً على عكس نظرية الأضلاع المتقابلة في متوازي الأضلاع فإنه
حتى يكون الشكل الرباعي PQRS متوازي أضلاع يجب أن تكون
.................................................................................................................................................................................................................................................................
أتحقق من فهمي :
أثبت أن تمثل رؤوس متوازي أضلاع.
الحل :
.................................................................................................................................................................................................................................................................
حل اسئلة وتمارين الدرس :
أتدرب وأحل المسائل:
أبين ما إذا كان كل شكل من الأشكال الرباعية الآتية متوازي أضلاع أم لا ، مبرراً إجابتي :
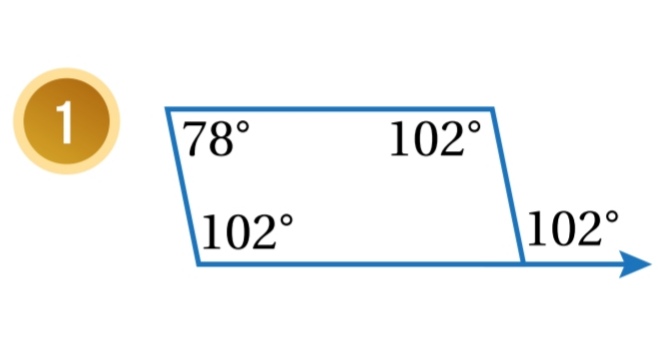
نلاحظ أن :
يكون حسب عكس نظرية الزوايا المتقابلة في متوازي الأضلاع ، إذن الشكل متوازي أضلاع
.................................................................................................................................................................................................................................................................
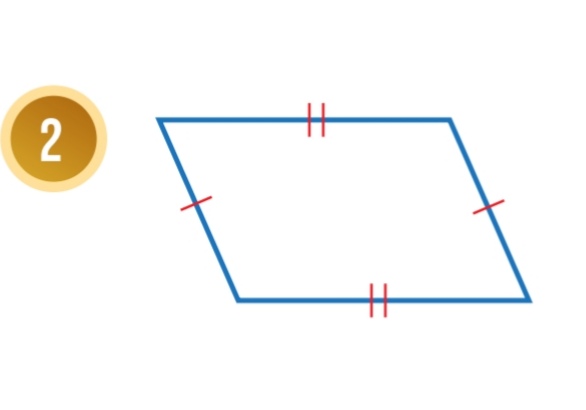
متوازي أضلاع حسب عكس نظرية الأضلاع المتقابلة في متوازي الأضلاع
.................................................................................................................................................................................................................................................................
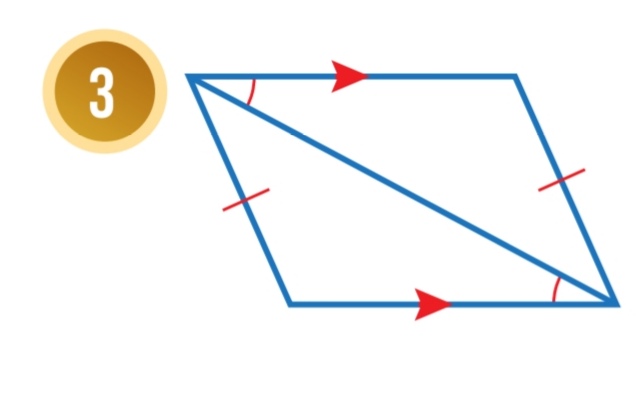
متوازي أضلاع حسب نظرية الأضلاع المتوازية والمتطابقة
.................................................................................................................................................................................................................................................................
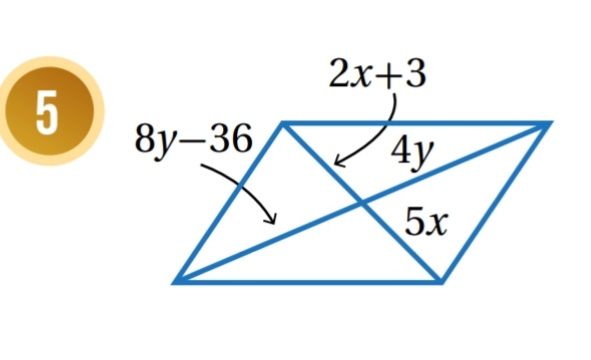
أجد قيمتي x و y اللتين تجعلان كل شكل رباعي مما يأتي متوازي أضلاع:
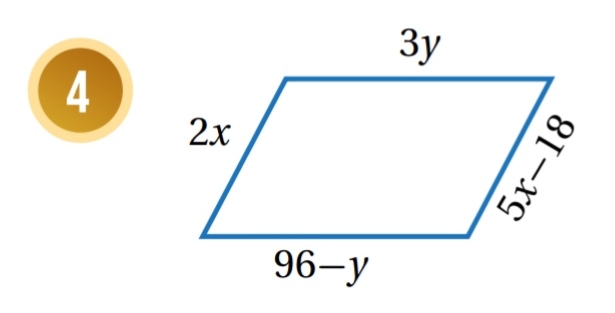
حسب عكس نظرية الأضلاع المتقابلة في متوازي الاضلاع
.................................................................................................................................................................................................................................................................
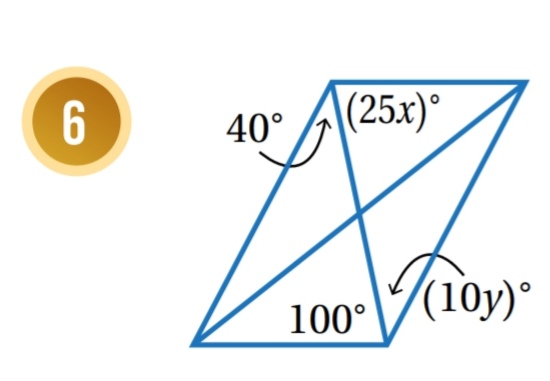
حسب عكس نظرية قطري متوازي الأضلاع
.................................................................................................................................................................................................................................................................
حتى يكون الشكل متوازي أضلاع يجب أن تكون :
.................................................................................................................................................................................................................................................................
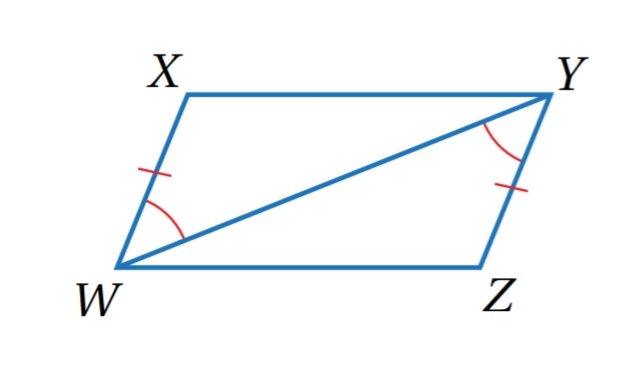
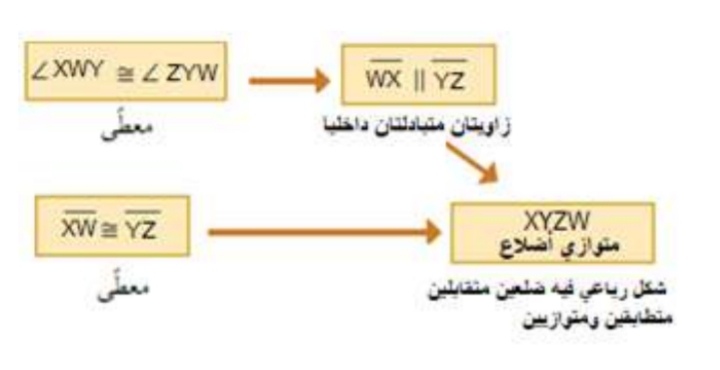
7) أستعمل المعلومات المعطاة في الشكل الآتي لكتابة برهان سهمي ، لأثبت أن الشكل الرباعي XYZW متوازي أضلاع.
.................................................................................................................................................................................................................................................................
8) أستعمل المعلومات المعطاة في الشكل الآتي لكتابة برهان سهمي ، لأثبت أن الشكل الرباعي LMNT متوازي أضلاع.
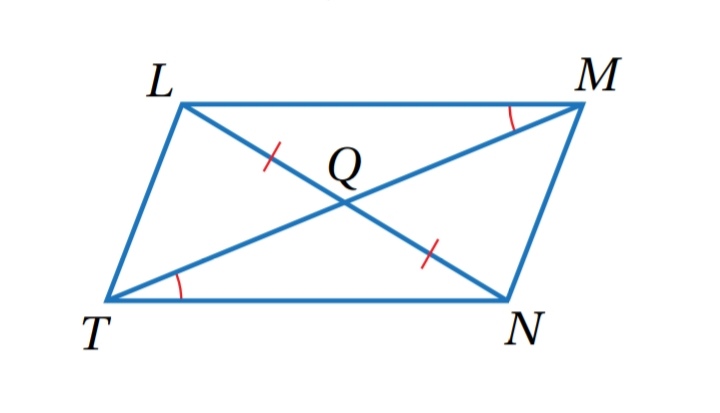
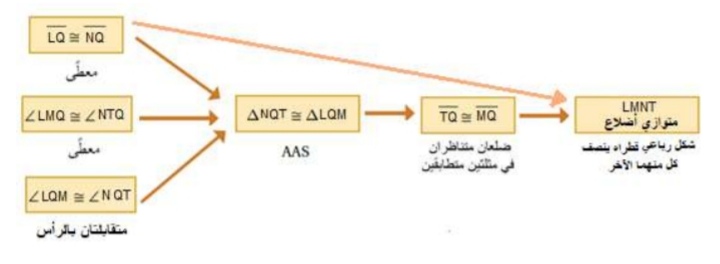
.................................................................................................................................................................................................................................................................
9) في الشكل الآتي ، إذا كان ، فأثبت أن RSTW متوازي أضلاع باستعمال البرهان ذي العمودين.
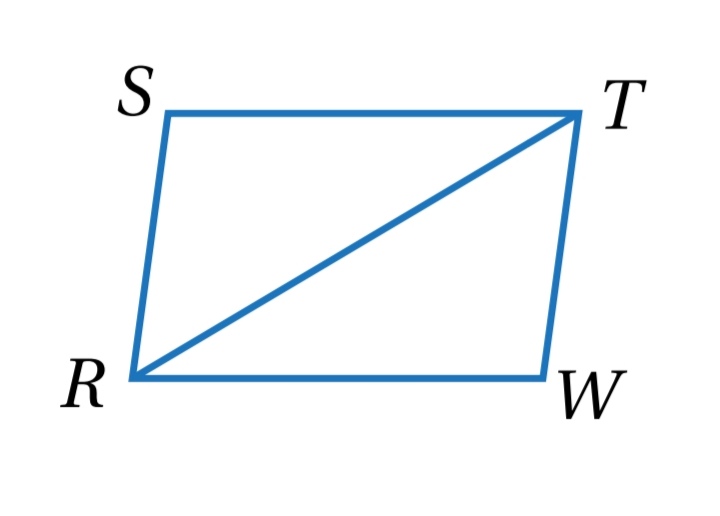

.................................................................................................................................................................................................................................................................
10) أستعمل المعلومات المعطاة في الشكل الآتي لكتابة برهان ذي عمودين، لأثبت أن الشكل الرباعي ANDL متوازي أضلاع .
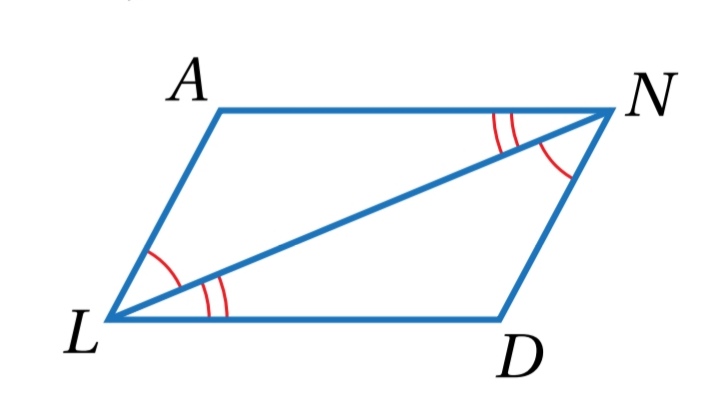
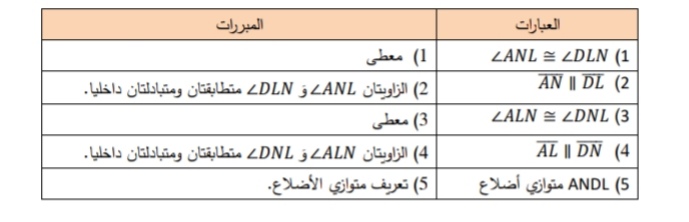
.................................................................................................................................................................................................................................................................
موقف سيارات: يبين الشكل المجاور موقفاً للسيارات، إذا كان
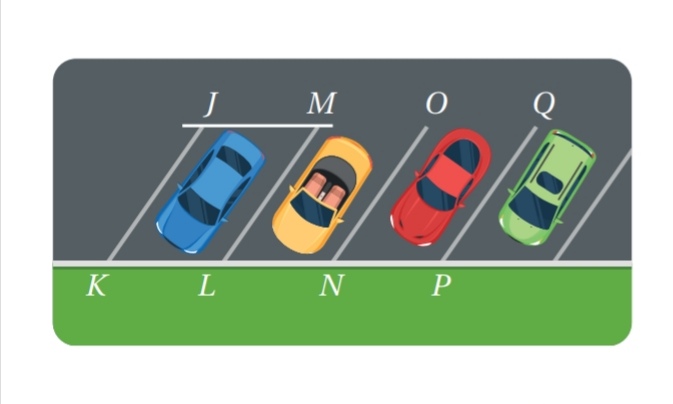
11) هل الجزء من الموقف JKLM متوازي أضلاع؟ أبرر إجابتي
الحل:
متوازي أضلاع لأن فيه كل ضلعين متقابلين متطابقين.
12) أجد كلاً من :
الحل:
13) هل ؟ أبرر إجابتي.
الحل :
لا يوجد ما يدل على أنهما متوازيان
.................................................................................................................................................................................................................................................................
14) حاسوب : تسمح معالجات نصوص حاسوبية عدة بكتابة الكلمة بالخط العادي أو الخط المائل . هل الحرف ( I ) ، متوازي أضلاع؟ أبرر إجابتي .
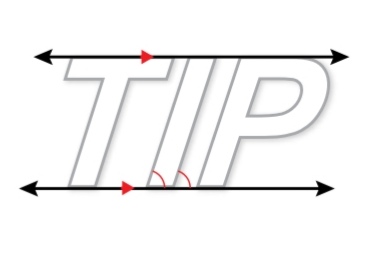
الحل:
نعم متوازي أضلاع ، لأنه معطى ضلعان متقابلان متوازيان، والضلعين الآخرين متوازيين لوجود زاويتين متناظرتين متطابقتين .
.................................................................................................................................................................................................................................................................
أمثل في المستوي الإحداثي الشكل الرباعي المعطاة إحداثيات رؤوسه في ما يأتي ، وأحدد ما إذا كان متوازي أضلاع أم لا ، مبرراً إجابتي
15) B ( -6 , -3 ) , C ( 2 , - 3 ) , E ( 4 , 4 ) , G ( -4 , 4 )
الحل:
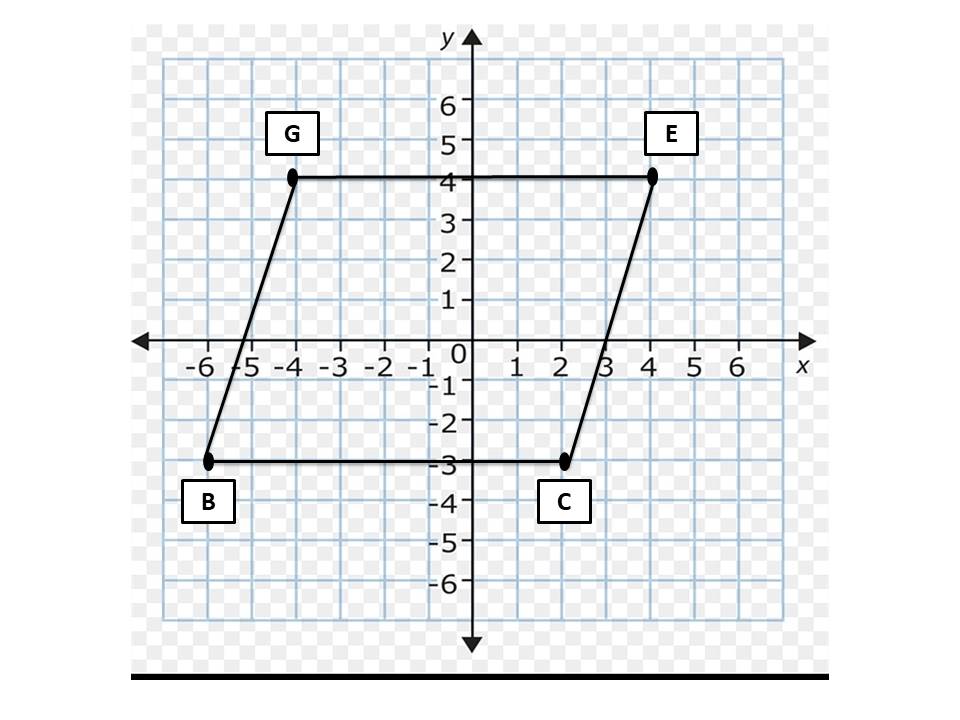
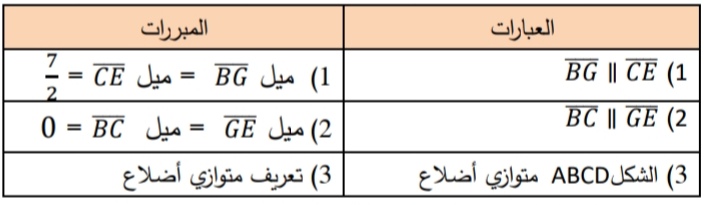
.........................................................................................................................
16) Q ( -3 , -6 ) , R ( 2 , 2 ) , S ( -1 , 6 ) , T ( -5 , 2 )
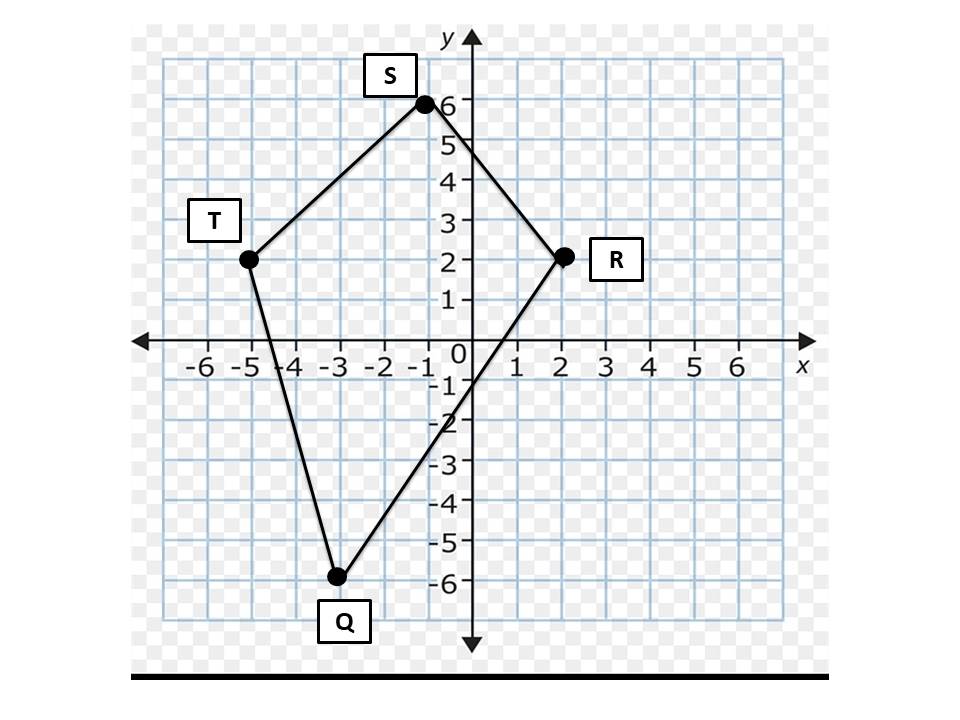
لا يوجد أضلاع متوازية ، الشكل ليس متوازي أضلاع.
.................................................................................................................................................................................................................................................................
تبرير : تمثل النقاط A , B , C في المستوي الإحداثي المجاور رؤوس شكل رباعي ، أجد إحداثيات النقطة الرابعة في كل من الحالات الآتية ، مبرراً إجابتي:
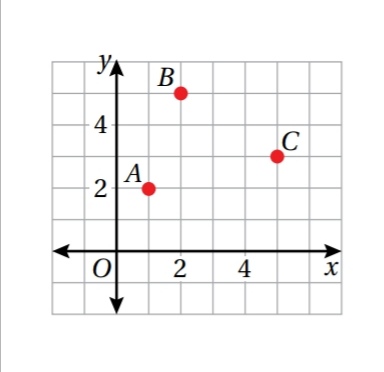
17) النقطة D حيث ABCD متوازي أضلاع
18) النقطة E حيث ABEC متوازي أضلاع
.................................................................................................................................................................................................................................................................
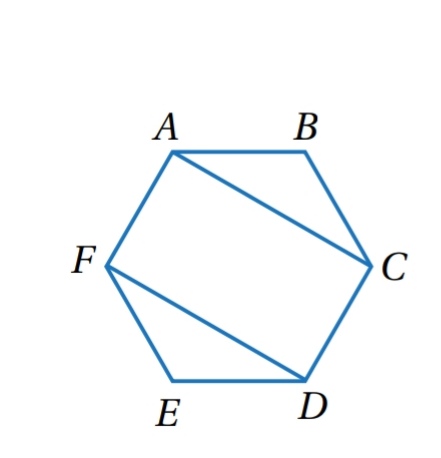
19) تبرير : أثبت أن الشكل الرباعي FACD متوازي أضلاع، علماً أن ABCDEF سداسي منتظم ، أبرر إجابتي
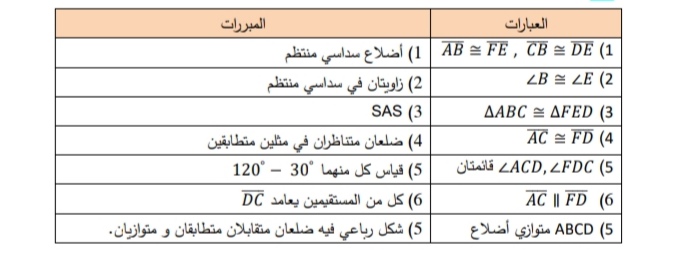
.................................................................................................................................................................................................................................................................
20) تحد : يبين الشكل المجاور متوازي الأضلاع LMNO ، وتمثل النقاط A , B , C , D منتصفات أضلاعه . أثبت أن الشكل ABCD متوازي أضلاع.
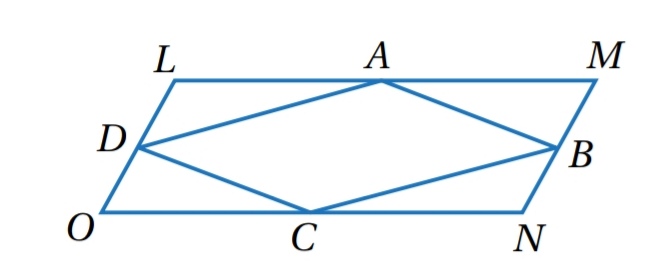
.................................................................................................................................................................................................................................................................
21) أكتب : كيف يمكن إثبات أن شكلاً رباعياً يمثل متوازي أضلاع ؟
يمكن إثبات أن الشكل الرباعي متوازي أضلاع إذا كان :
- كل ضلعين متقابلين فيه متوازيين
- كل ضلعين متقابلين فيه متطابقين
- كل زاويتين متقابلتين فيه متطابقتين
- قطراه ينصف كل منهما الآخر
- إذا كان فيه ضلعان متقابلان متوازيان ومتطابقان.
.................................................................................................................................................................................................................................................................
حل أسئلة كتاب التمارين :
أحدد النظرية التي يمكنني استعمالها لابين ان الشكل الرباعي في كل مما يأتي متوازي أضلاع :
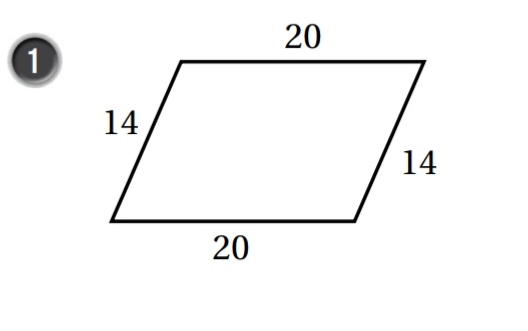
عكس نظرية الأضلاع المتقابلة في متوازي الأضلاع
.................................................................................................................................................................................................................................................................
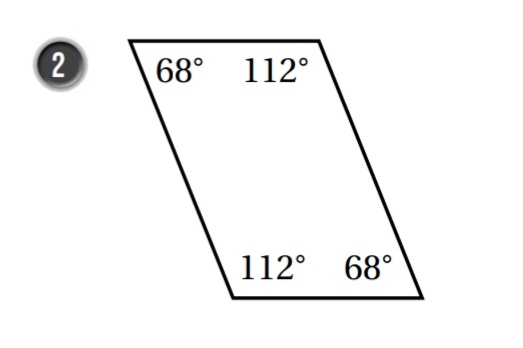
عكس نظرية الزوايا المتقابلة في متوازي الاضلاع
.................................................................................................................................................................................................................................................................
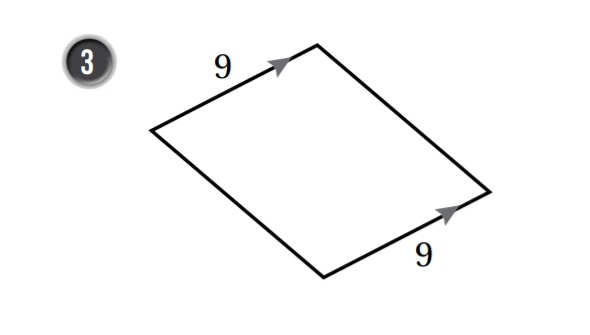
نظرية الاضلاع المتوازية والمتطابقة
.................................................................................................................................................................................................................................................................
أجد قيمة x و y اللتين تجعلان كل شكل رباعي مما يأتي متوازي أضلاع :
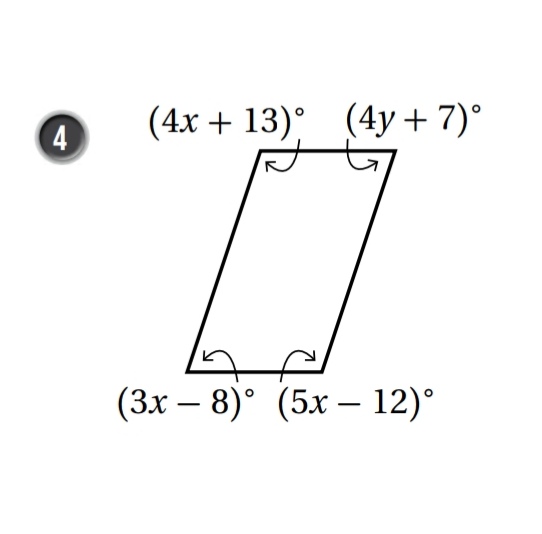
الحل :
حسب عكس نظرية الزوايا المتقابلة في متوازي الأضلاع
:فيكون x أعوض 25 بدلاً من
.................................................................................................................................................................................................................................................................
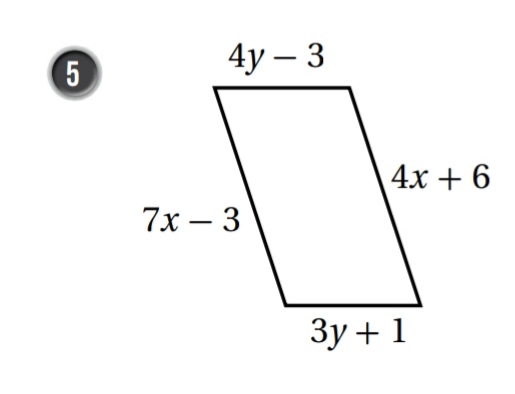
الحل:
حسب عكس نظرية الأضلاع المتقابلة في متوازي الأضلاع
.................................................................................................................................................................................................................................................................
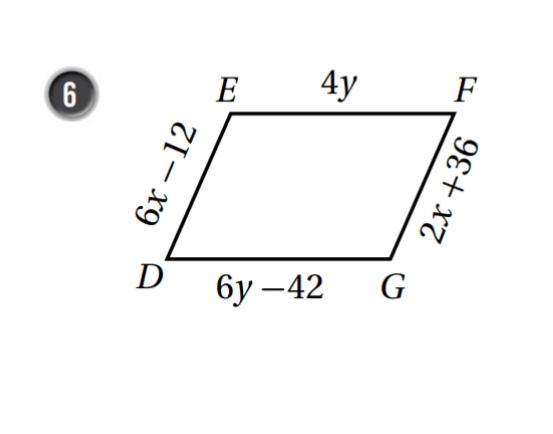
الحل :
حسب عكس نظرية الأضلاع المتقابلة في متوازي الأضلاع
.................................................................................................................................................................................................................................................................
7) أستعمل المعلومات المعطاة في الشكل المجاور لكتابة برهان سهمي ، لأثبت أن الشكل الرباعي ABCD متوازي أضلاع :
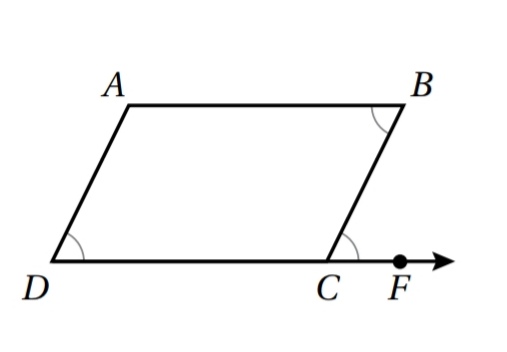
الحل :
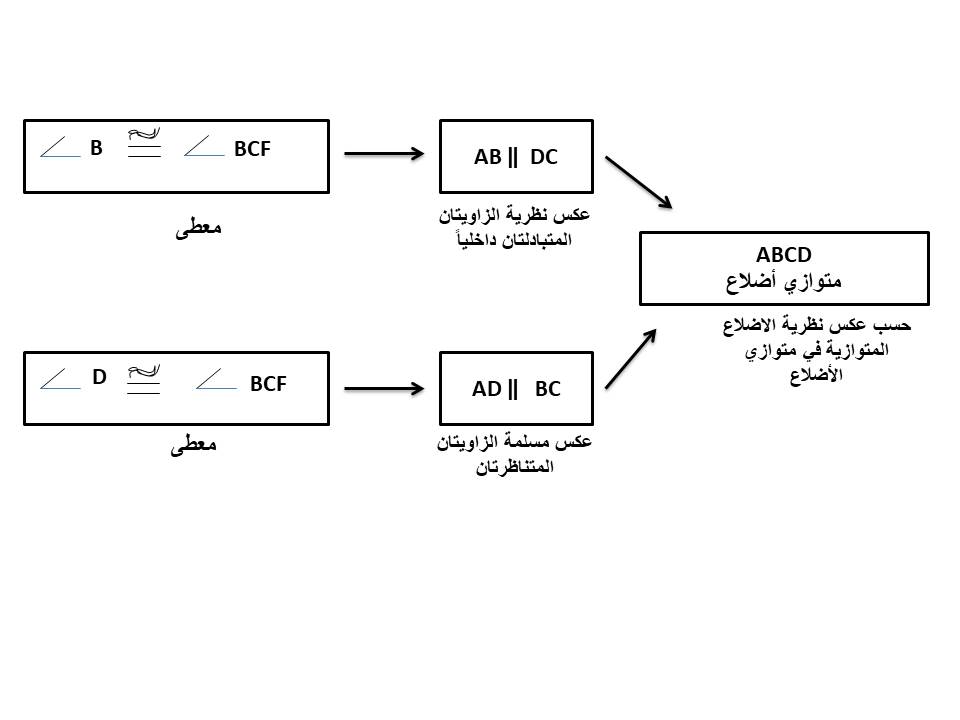
.................................................................................................................................................................................................................................................................
8) أمثل الرؤوس في المستوي الإحداثي ، ثم أحدد إحداثيات الرأس D الذي يجعل الشكل الرباعي ABCD متوازي أضلاع مبرراً إجابتي :
الحل :
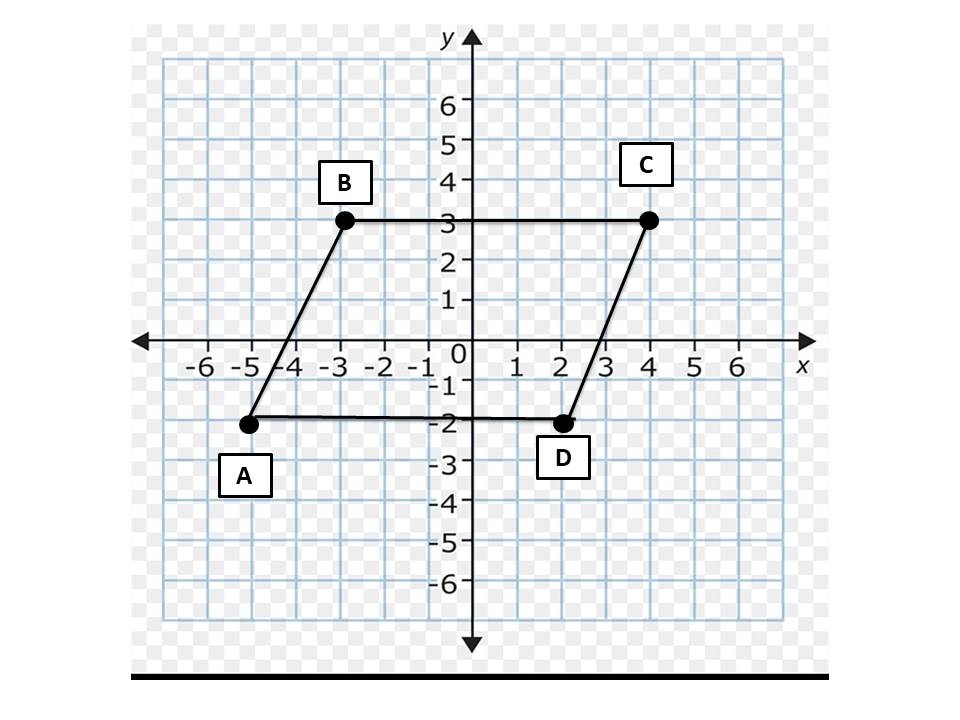
ألاحظ من الشكل أن BC = 7
حسب عكس نظرية الأضلاع المتقابلة في متوازي الأضلاع
بالتمثيل على الشكل تكون D ( 2 , -2 )
مع العلم بأن حسب عكس نظرية الأضلاع المتوازية في متوازي الأضلاع .
.................................................................................................................................................................................................................................................................
9) يقول عماد : إنه يمكن إثبات أن الشكل الرباعي JKLM متوازي أضلاع باستعمال عكس نظرية الأضلاع المتطابقة في متوازي الأضلاع ، أكتشف الخطأ في قول عماد .
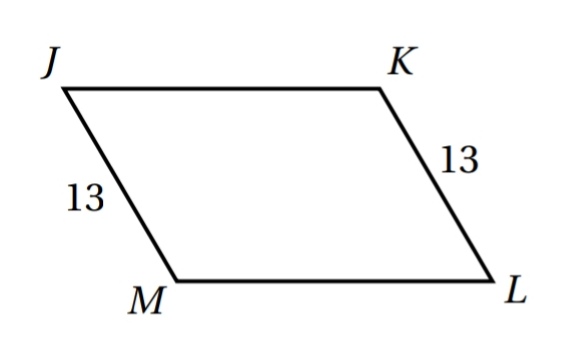
الحل :
الخطأ في قول عماد:
حسب عكس نظرية الأضلاع المتطابقة في متوازي الأضلاع يكون:
كل ضلعين متقابلين متطابقين في متوازي الأضلاع
والضعين JK و ML غي متطابقين بالضرورة
.................................................................................................................................................................................................................................................................