فكرةُ الدّرس
- أجمعُ عددين صحيحين.
- أحُلُّ مسائل حياتيّةً عن جمع الأعداد الصّحيحة.
المُصطلحاتُ: النّظيرُ الجمعيُّ.
أولا: جمع عددين صحيحين لهُما الإشارةُ نفسُها
- ويكون إيجاد الناتج عن طريق جمع القيم المُطلقة للعددين، ووضع إشارة أحدهما في النّاتج.
مثال
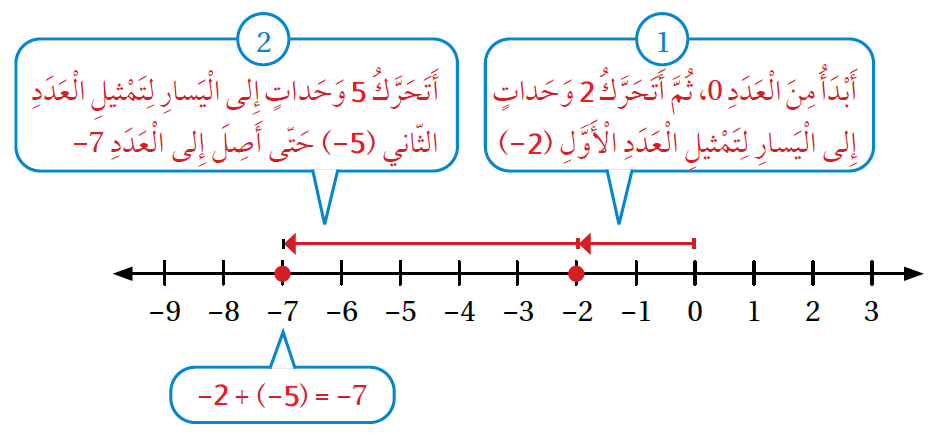
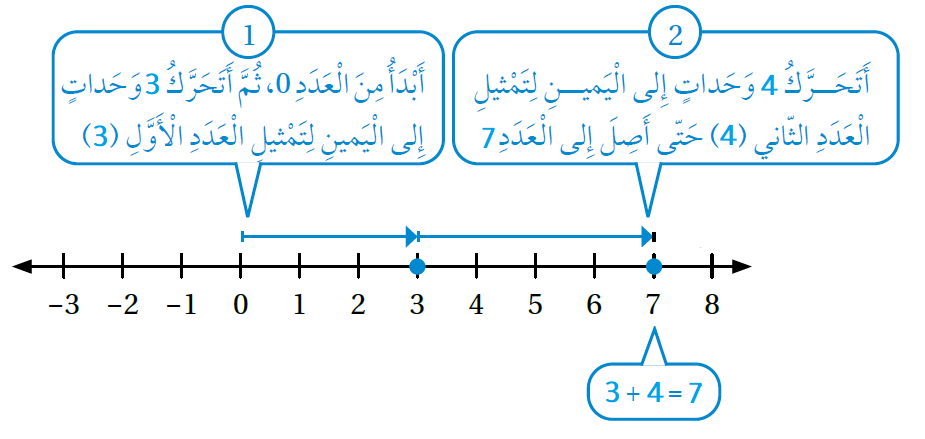
أجدُ ناتج كُلٍّ ممّا يأتي، ثُمّ أتحقّقُ من صحّة الحلّ باستعمال خطّ الأعداد:
| نجمع | نجمع |
| للتحقق: نستعمل خط الأعداد | للتحقق: نستعمل خط الأعداد |
 |
 |
ثانيا: جمع عددين صحيحين مُختلفي الإشارة
- ويكون إيجاد الناتج بطرح القيمة المُطلقة الصُّغرى من القيمة المُطلقة الكُبرى، ووضع إشارة العدد الّذي قيمتُهُ المُطلقةُ أكبرُ في النّاتج.
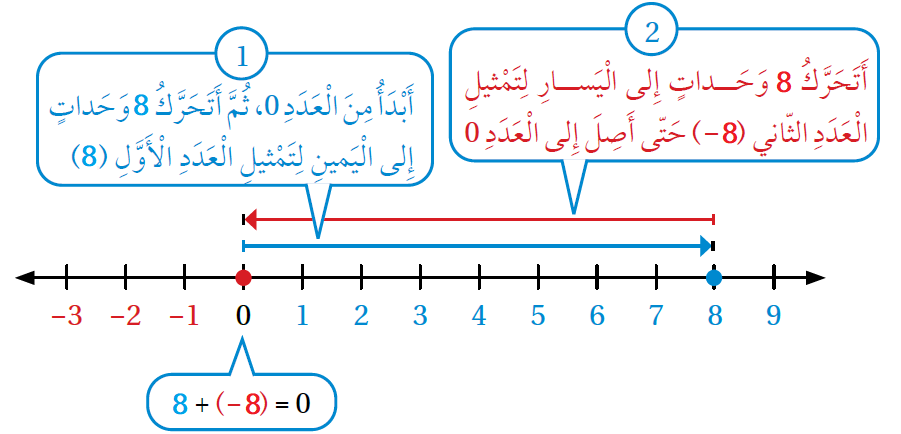
- عند جمع عددٍ ومعكوسه يكونُ النّاتجُ صفرًا، ويُسمّى كُلٌّ منهُما أيضًا نظيرًا جمعيًّا للآخر.
مثال
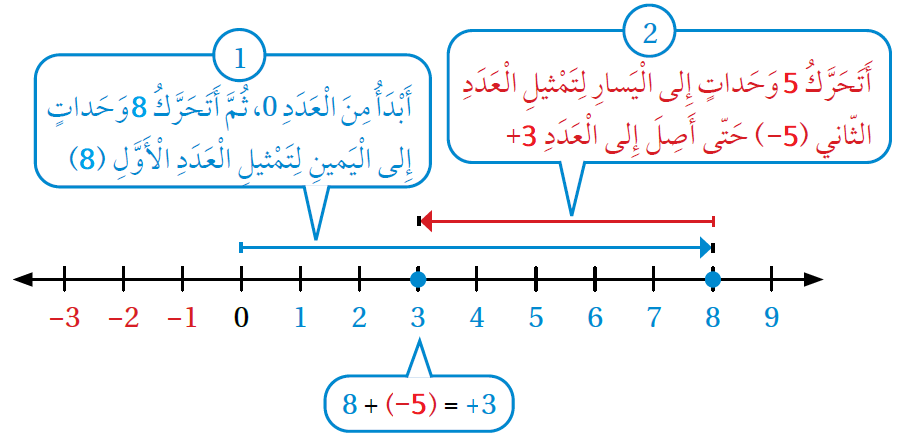
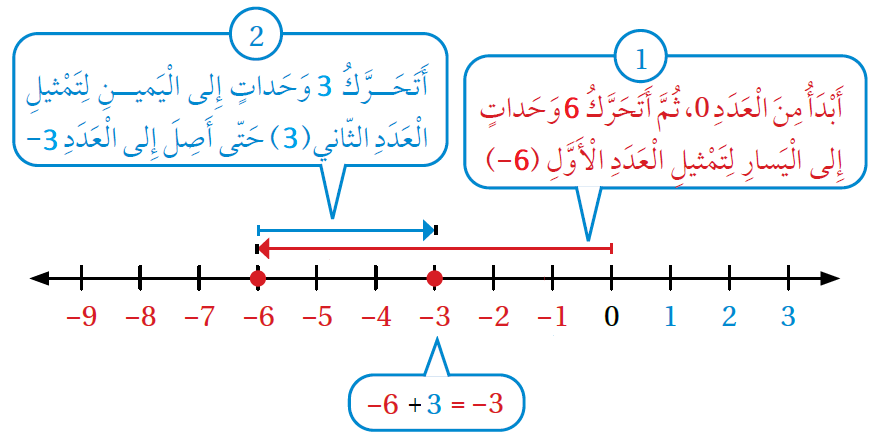
أجدُ ناتج كُلٍّ ممّا يأتي، ثُمّ أتحقّقُ من صحّة الحلّ باستعمال خطّ الأعداد:
| لِذا نطرح |5-| من |8| | لِذا نطرح |3| من |6-| |
| للتحقق: نستعمل خط الأعداد | للتحقق: نستعمل خط الأعداد |
 |
 |
| المجموعُ يساوي صِفرًا؛ لأنَّ كلًّ مِنهُما نَظيرٌ جمعِيٌّ لِلآخَر. | |
| للتحقق: نستعمل خط الأعداد | |
 |
|
مثال أراد حارسُ المرمى أحمدُ التقاط الكُرة، فجرى مسافة 11m إلى الأمام بدءًا من المرمى، ثُمّ عاد مسافة 7m إلى الخلف. كم مترًا يبعدُ عن المرمى؟ الجواب يُمكنُ إيجادُ بُعد أحمد عن المرمى بجمع المسافة الّتي ركض فيها إلى الأمام مع المسافة الّتي ركض فيها إلى الخلف، ويُمثّلُ العددُ الموجبُ (11+) الأمتار المقطوعة إلى الأمام، ويُمثّلُ العددُ السّالبُ (7-) الأمتار المقطوعة إلى الخلف، بدءًا بالمرمى؛ أي إنّ المطلوب إيجادُهُ هُو |
 |
||
إذن، بُعدُ أحمد عن المرمى هُو 4m |