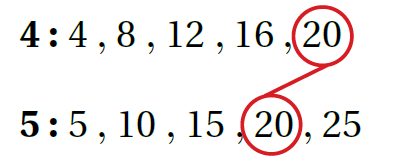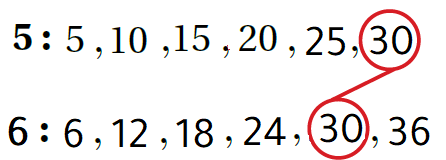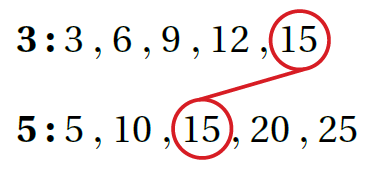رياضيات فصل أول

فكرةُ الدّرس: أجدُ ناتج جمع الكُسور وطرحها في أبسط صورةٍ.

تعلّمتُ سابقًا جمع كسرين مُتشابهين وطرحهُما، وهُما كسران مقاماهُما مُتساويان. 

مثل: $\frac{3}{7}+\frac{2}{7}=\frac{5}{7}$   ،    $\frac{10}{23}-\frac{1}{23}=\frac{9}{23}$

ولجمع كسرين غير مُتشابهين:

1. أُوحّدُ المقامين بالبحث عن المُضاعف المُشترك الأصغر لمقامي الكسرين الأصليّين
2. أكتُبُ الكسرين بمقامين جديدين، كُلٌّ منهُما يُساوي المُضاعف المُشترك الأصغر لمقامي الكسرين الأصليّين.

مثال

أجدُ ناتج كُلٍّ ممّا يأتي في أبسط صورةٍ:

$\mathbf{1}\mathbf{)} \frac{3}{4}+\frac{3}{5}$

أجدُ المُضاعف المُشترك الأصغر للمقامين 4 و 5 لجعل الكسرين مُتشابهين فنكتب مضاعفات كل عدد. إذن، المُضاعفُ المُشتركُ الأصغرُ هُو 20

$\frac{3\times 5}{4\times 5}+\frac{3\times 4}{5\times 4}=\frac{15}{20}+\frac{12}{20}=\frac{27}{20}$             أجمعُ البسطين، مع الحفاظ على المقامين.

$\frac{3}{4}+\frac{3}{5}=\frac{27}{20}=1\frac{7}{20}$ أكتُبُ النّاتج في صورة عددٍ كسريٍّ ليكون بأبسط صورة.

$\mathbf{2}\mathbf{)} \frac{2}{5}+\frac{1}{6}$

أجدُ المُضاعف المُشترك الأصغر للمقامين 5 و 6 لجعل الكسرين مُتشابهين فنكتب مضاعفات كل عدد. إذن، المُضاعفُ المُشتركُ الأصغرُ هُو 30

$\frac{2\times 6}{5\times 6}+\frac{1\times 5}{6\times 5}=\frac{12}{30}+\frac{5}{30}=\frac{17}{30}$أجمعُ البسطين، مع الحفاظ على المقامين.

---

مثلما جمعتُ كسرين غير مُتشابهين يُمكنُني طرحُ كسرين غير مُتشابهين، وذلك بتوحيد المقامين باستعمال المُضاعف المُشترك الأصغر لهُما.

مثال

أجدُ ناتج كُلٍّ ممّا يأتي في أبسط صورةٍ:

$\mathbf{1}\mathbf{)}\mathbf{ }\frac{4}{5}-\frac{2}{3}$

أجدُ المُضاعف المُشترك الأصغر للمقامين 3 و 5 لجعل الكسرين مُتشابهين فنكتب مضاعفات كل عدد. إذن، المُضاعفُ المُشتركُ الأصغرُ هُو 15

$\frac{4\times 3}{5\times 3}-\frac{2\times 5}{3\times 5}=\frac{12}{15}-\frac{10}{15}=\frac{2}{15}$

---

أستعملُ جمع الكُسور العاديّة وطرحها في كثيرٍ من المواقف الحياتيّة، مثل المكاييل

مثال أكوابٌ قياسيّةٌ: استعملت علياءُ أكوابًا قياسيّةً لكيل $\frac{3}{4}$ كوبٍ من زيت جوز الهند، ثُمّ قرّرت إنقاص $\frac{1}{3}$ كوبٍ من الكمّيّة المكيلة. ما كمّيّةُ زيت جوز  الهند المكيلةُ؟  الجواب
لحساب الكمّيّة المكيلة، أطرحُ الكسر  $\frac{1}{3}$ من الكسر  $\frac{3}{4}$:
أُوحّدُ المقامين بإيجاد المُضاعف المُشترك الصغر لهُما  $\frac{3\times 3}{4\times 3}-\frac{1\times 4}{3\times 4}=\frac{9}{12}-\frac{4}{12}=\frac{5}{12}$
إذن، كمّيّةُ زيت الهند المكيلة هي $\frac{5}{12}$ كوب.