رياضيات فصل أول

الثامن

الشرح الملخص أوراق العمل حل اسئلة الدرس النتاجات

حالاتٌ خاصةٌ مِنْ ضربِ المقاديرِ الجبريةِ

أتحقق من فهمي 1 : أجدُ ناتجَ كلٍّ ممّا يأتي.

$3) {(2 c + 10)}^{2}$

الحل :

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

${(2 c + 10)}^{2} = {(2 c)}^{2} + (2 \times 2 c \times 10) + {(10)}^{2}$

$= 2 c^{2} + 40 c + 100$

${4) (d^{2} + 4)}^{2}$

الحل :

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

${(d^{2} + 4)}^{2} = {(d^{2})}^{2} + (2 \times d^{2} \times 4) + {(4)}^{2}$

$= d^{4} + 8 d^{2} + 16$

أتحقق من فهمي 2 : أجدُ ناتجَ كلٍّ ممّا يأتي.

$3) {(7 t^{2} - 1)}^{2}$

الحل :

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

${(7 t^{2} - 1)}^{2} = {(7 t^{2})}^{2} - (2 \times 7 t^{2} \times 1) + {(1)}^{2}$

$= 49 t^{4} - 14 t^{2} + 1$

$4) {(x^{3} - 4 y^{2})}^{2}$

الحل :

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

${(x^{3} - 4 y^{2})}^{2} = {(x^{3})}^{2} - (2 \times x^{3} \times 4 y^{2}) + {(4 y^{2})}^{2}$

$= x^{6} - 8 x^{3} y^{2} + 16 y^{4}$

أتحقق من فهمي 3 : أجدُ ناتجَ كلٍّ ممّا يأتي.

$3) (6 w + d^{4}) (6 w - d^{4})$

الحل :

$(a - b) (a + b) = a^{2} - b^{2}$

$= (6 w + d^{4}) (6 w - d^{4}) = {(6 w)}^{2} - {(d^{4})}^{2}$

$= 36 w^{2} - d^{8}$

$4) (x^{3} + 3 h^{7}) (x^{3} - 3 h^{7})$

الحل :

$(a - b) (a + b) = a^{2} - b^{2}$

$= (x^{3} + 3 h^{7}) (x^{3} - 3 h^{7}) = {(x^{3})}^{2} - {(3 h^{7})}^{2}$

$= x^{6} - 9 h^{14}$

أتحقق من فهمي 4 : نجارةٌ: يبيّنُ الشكلُ المجاورُ أبعادَ لوحٍ خشبيٍّ مربعِ الشكلِ طولُ ضلعِهِ x سنتيمترًا. إذا قُصَّ شريطٌ عرضُهُ 3cm من حافتَيِ اللوحِ مثلَما يظهرُ في الشكلِ، فأحسبُ مساحةَ المربع المتبقي مِنَ اللوحِ بدلالةِ x .

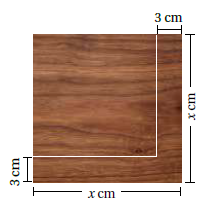
الحل : نحددُ طولَ ضلعِ اللوح الخشبي المتبقي بعدَ القصِّ.

طولُ ضلع اللوح الخشبي الأصلي x سنتيمترًا قُصَّ منها 3cm ، بمحاذاةِ حافتي اللوح.

إذنْ، أصبحَ طولُ الضلعِ (x-3) سنتيمتراً كما هو موضح في الشكل.

ولحساب المساحة نضرب الطول بالعرض كالتالي :

$A = S \times S$

$A = S^{2} = {(x - 3)}^{2}$

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

${(x - 3)}^{2} = x^{2} - (2 \times x \times 3) + 3^{2}$

$= x^{2} - 6 x + 9$

أتحقق من فهمي 5 : أستعملُ الحسابَ الذهنيَّ لأجدَ ناتجَ كلٍّ ممّا يأتي:

$1) 52^{2}$

الحل :

$52^{2} = {(50 + 2)}^{2}$

$= 50^{2} + (2 \times 50 \times 2) + 2^{2}$

$= 2500 + 200 + 4 = 2704$

$2) 49^{2}$

الحل :

$49^{2} = {(40 + 9)}^{2}$

$= 40^{2} + (2 \times 40 \times 9) + 9^{2}$

$= 1600 + 720 + 81 = 2401$

أتدرب وأحل مسائل :

أجدُ ناتجَ كلٍّ ممّا يأتي:

$1) {(w + 2)}^{2}$

الحل :

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

${(w + 2)}^{2} = {(w)}^{2} + (2 \times w \times 2) + {(2)}^{2}$

$= w^{2} + 4 w + 4$

$2) {(x - 11)}^{2}$

الحل :

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

${(x - 11)}^{2} = {(x)}^{2} - (2 \times x \times 11) + {(11)}^{2}$

$= x^{2} - 22 x + 121$

$3) {(4 m^{3} - 5 y)}^{2}$

الحل :

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

${(4 m^{3} - 5 y)}^{2} = {(4 m^{3})}^{2} - (2 \times 4 m^{3} \times 5 y) + {(5 y)}^{2}$

$= 16 m^{6} - 40 m^{3} y + 25 y^{2}$

$4) (w^{2} - 7) (w^{2} - 7)$

الحل :

$(w^{2} - 7) (w^{2} - 7)$

$= {(w^{2} - 7)}^{2} = {(w^{2})}^{2} - (2 \times w^{2} \times 7) + {(7)}^{2}$

$= w^{4} - 14 w^{2} + 49$

$5) (5 a + 4) (5 a - 4)$

الحل :

$(a - b) (a + b) = a^{2} - b^{2}$

$= (5 a + 4) (5 a - 4) = {(5 a)}^{2} - {(4)}^{2}$

$= 25 a^{2} - 16$

$6) (x^{2} + 7 y^{4}) (x^{2} - 7 y^{4})$

الحل :

$(a - b) (a + b) = a^{2} - b^{2}$

$= (x^{2} + 7 y^{4}) (x^{2} - 7 y^{4}) = {(x^{2})}^{2} - {(7 y^{4})}^{2}$

$= x^{4} - 49 y^{8}$

7) هندسةٌ: بركةُ سباحةٍ مستطيلةُ الشكلِ، طولها بالمتر (3x+6) وعرضها (3x-6) ، أجد مساحتها بدلالة x وبأبسط صورة .

الحل :

نجد مساحة البركة بضرب الطول بالعرض كالتالي :

$(a - b) (a + b) = a^{2} - b^{2}$

$= (3 x - 6) (3 x + 6)$

$= {(3 x)}^{2} - {(6)}^{2} = 9 x^{2} - 36$

حسابٌ ذهنيٌّ: أستعملُ الحسابَ الذهنيَّ لأجدَ ناتجَ كلٍّ ممّا يأتي:

$8) 88^{2}$

الحل :

$88^{2} = {(80 + 8)}^{2}$

$= 80^{2} + (2 \times 80 \times 8) + 8^{2}$

$= 6400 + 1280 + 64 = 7744$

$9) 403^{2}$

الحل :

$403^{2} = {(400 + 3)}^{2}$

$= 400^{2} + (2 \times 400 \times 3) + 3^{2}$

$= 160000 + 2400 + 9 = 162409$

$10) 37^{2}$

الحل :

$37^{2} = {(30 + 7)}^{2}$

$= 30^{2} + (2 \times 30 \times 7) + 7^{2}$

$= 900 + 420 + 49 = 1369$

11) يبيّنُ الشكلُ المجاورُ جدارًا مربعَ الشكلِ تتوسطُهُ نافذةٌ. أعبّرُ عَنْ مساحةِ الجدارِ بدلال x بطريقتين مختلفتين

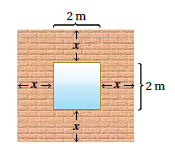
الحل :

الحل : نطرح (المساحة الكلية - مساحة النافذة)

طول الضلع للجدار (2x+x)

وطول ضلع النافذة (x)

الآن نحسب المساحة المتبقية من الجدار كالتالي :

${(2 x + 2)}^{2} - 2^{2} = 4 x^{2} + 8 x + 4 - 4$

$= 4 x^{2} + 8 x = 4 x (x + 2)$

12) علومٌ: لوحةٌ معدنيةٌ مربعةُ الشكلِ، طولُ ضلعِها بالسنتيمتر (w) ، إذا تعرضَتْ للحرارةِ فتمدّدَتْ وازدادَ طولُ ضلعِها بمقدار 0.02cm ، فأجدُ مساحةَ اللوحةِ بعدَ التمدّدِ بدلالةِ w

الحل : طول ضلع اللوحة بعد التمدد : (w+0.02) , وعليه نجد المساحة كالتالي :

$A = S \times S = S^{2} = {(w + 0.02)}^{2}$

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

${(w + 0.02)}^{2} = w^{2} + (2 \times w \times 0.02) + 0 . 02^{2}$

$= w^{2} - 0.04 w + 0.0004$

قياسٌ: أجدُ مساحةَ كلِّ شكلٍ ممّا يأتي بدلالةِ x

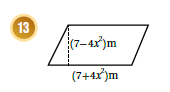
ملاحظة : الشكل يمثل متوازي أضلاع ،

ولنجد مساحة متوازي الأضلاع نضرب طول القاعدة في الارتفاع كالتالي :

$A = s \times h$

$= (7 + 4 x^{2}) (7 - 4 x^{2}) = 49 - 16 x^{4}$

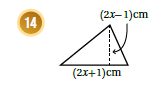
ملاحظة : الشكل يمثل مثلث ،

ولنجد مساحة المثلث نضرب ( 0.5 * طول القاعدة * الارتفاع ) كالتالي :

$\frac{1}{2} \times (2 x + 1) (2 x - 1)$

$= \frac{1}{2} \times (4 x^{2} - 1) = 2 x^{2} - \frac{1}{2}$

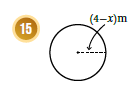
ملاحظة : الشكل يمثل دائرة ،

ولنجد مساحة الدائرة نستخدم القانون $A = {πr}^{2}$ ، حيث r تمثل نصف القطر . كالتالي :

$A = {πr}^{2} = π {(4 - x)}^{2}$

$= π (16 - 8 x + x^{2})$

16) أكتشفُ المختلفَ: أحددُ العبارةَ المختلفةَ عَنْ بقيةِ العباراتِ:

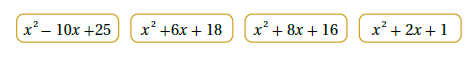
الحل:

بالنظر إلى العبارات الأربع نلاحظ أن العبارة الثانية مختلفة وذلك بسبب أن الحد الثابت (الحد الثالث) ليس مربعاً كاملاً .

17) تحدٍّ: هَلْ توجدُ قاعدةٌ لحسابِ ${(x - y)}^{3}$

نعم يوجد ، ويمكن استنتاجها بضرب المقدار بنفسه مكرر 3 مرات كالتالي :

${(x - y)}^{3} = (x - y) (x - y) (x - y)$

$= (x - y) {(x - y)}^{2} = (x - y) (x^{2} - 2 x y + y^{2})$

18) تبريرٌ: أبيّنُ أنَّ مساحتَيِ الجزأَينِ المظللَينِ في الشكلَينِ المجاورَينِ متساويتانِ أَمْ لا. أبرّرُ إجابتي

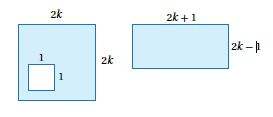
نحسب مساحة كل شكل بشكل مستقل ثم نقارن .

مساحة الشكل الأيمن :

$A = S 1 \times S 2$

$= (2 k + 1) (2 k - 1^{2}) = 4 k^{2} - 1$

مساجة الشكل الأيسر (مساحة المربع الكبير - مساحة المربع الصغير) :

$A = A 1 - A 2$

$= {(2 k)}^{2} - 1^{2} = 4 k^{2} - 1$

إذن المساحتان متساويتان .

19) أكتبُ فقرةً أبيّنُ فيها كيفَ أجدُ مربعَ مجموعِ حدَّينِ.

الحل :

لإيجاد مربع مجموع حدين :

.b مضافًا إليهِ مربعُ b في a مضافًا إليهِ مِثْلا حاصِلِ ضربِ a يساوي مربعَ (a + b) مربع

أو حسب الصيغة : ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

أسئلة كتاب التمارين :

أجدُ ناتجَ كلٍّ ممّا يأتي بأبسطِ صورةٍ:

$1) {(h - 10)}^{2}$

الحل :

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

${(h - 10)}^{2} = {(h)}^{2} - (2 \times h \times 10) + {(10)}^{2}$

$= h^{2} - 20 h + 100$

$2) {(y - 2 x)}^{2}$

الحل :

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

${(y - 2 x)}^{2} = {(y)}^{2} - (2 \times y \times 2 x) + {(2 x)}^{2}$

$= y^{2} - 4 x y + 4 x^{2}$

$3) {(5 - 3 x)}^{2}$

الحل :

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

${(5 - 3 x)}^{2} = {(5)}^{2} - (2 \times 5 \times 3 x) + {(3 x)}^{2}$

$= 25 - 30 x + 9 x^{2}$

أجدُ ناتجَ كلٍّ ممّا يأتي بأبسطِ صورةٍ:

$4) (5 c + 2 b) (5 c + 2 b)$

الحل :

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

${(5 c + 2 b)}^{2} = {(5 c)}^{2} + (2 \times 5 c \times 2 b) + {(2 b)}^{2}$

$= 25 c^{2} + 20 b c + 4 b^{2}$

$5) {(r + 8)}^{2}$

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

${(r + 8)}^{2} = {(r)}^{2} + (2 \times r \times 8) + {(8)}^{2}$

$= r^{2} + 16 r + 64$

$6) {(2 n + 3)}^{2}$

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

${(2 n + 3)}^{2} = {(2 n)}^{2} + (2 \times 2 n \times 3) + {(3)}^{2}$

$= 4 n^{2} + 12 n + 9$

أجدُ ناتجَ كلٍّ ممّا يأتي بأبسطِ صورةٍ:

$7) (m - 7) (m + 7)$

$(a - b) (a + b) = a^{2} - b^{2}$

$= (m - 7) (m + 7) = {(m)}^{2} - {(7)}^{2}$

$= m^{2} - 49$

$8) (2 d - 3) (2 d + 3)$

$= (a - b) (a + b) = a^{2} - b^{2}$

$= (2 d - 3) (2 d - 3) = {(2 d)}^{2} - {(3)}^{2}$

$= 4 d^{2} - 9$

$9) (2 + x y) (2 - x y)$

$= (a - b) (a + b) = a^{2} - b^{2}$

$= (2 + x y) (2 - x y) = {(2)}^{2} - {(xy)}^{2}$

$= 4 - x^{2} y^{2}$

حسابٌ ذهنيٌّ: أستعملُ الحسابَ الذهنيَّ لأجدَ ناتجَ كلٍّ ممّا يأتي:

$10) 103^{2}$

$103^{2} = {(100 + 3)}^{2}$

$= 100^{2} + (2 \times 100 \times 3) + 3^{2}$

$= 10000 + 600 + 9 = 10609$

$11) 1007^{2}$

$1007^{2} = {(1000 + 7)}^{2}$

$= 1000^{2} + (2 \times 1000 \times 7) + 7^{2}$

$= 1000000 + 14000 + 49 = 1014049$

$12) 95^{2}$

$95^{2} = {(90 + 5)}^{2}$

$= 8100 + (2 \times 90 \times 5) + 5^{2}$

$= 8100 + 900 + 25 = 9025$

$13) 991^{2}$

$991^{2} = {(990 + 1)}^{2}$

$= 990^{2} + (2 \times 990 \times 1) + 1^{2}$

$= 980100 + 1980 + 1 = 982081$

$14) 49 \times 51 = 2499$

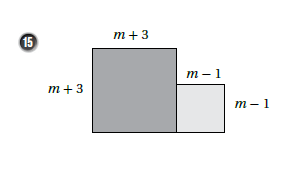
نجد مساحة كل مربع على حدة ثم نجمع المساحتين كالتالي :

$A 1 + A 2 = {(m + 3)}^{2} + {(m - 1)}^{2}$

$= ((m^{2} + (2 \times m \times 3) + 3^{2})) + (m^{2} - (2 \times m \times 1) + 1^{2})$

$= m^{2} + 6 m + 9 + m^{2} - 2 m + 1$

$= 2 m^{2} + 4 m + 10$

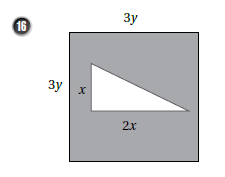ملاحظة :

مساحة المثلث تساوي : $\frac{1}{2} \times b \times h$ ، حيث b : طول قاعدة المثلث ، و h : ارتفاع المثلث

نجد مساحة المربع ثم مساحة المثلث تم نطرح :

( مساحة المربع-مساحة المثلث) كالتالي :

$A 1 - A 2 = {(3 y)}^{2} - (\frac{1}{2} \times 2 x \times x)$

$= 9 y^{2} - x^{2}$

سياراتٌ: يبيّنُ الشكلُ المجاورُ نافذةَ سيارةٍ على شكلِ شبهِ منحرفٍ.أكتبُ مساحةَ النافذةِ بدلالةِ x ، ثُمَّ أجدُ المساحةَ عندَما x=56

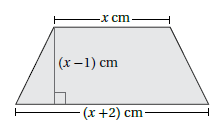
ملاحظة :

مساحة شبه المنحرف تساوي : $\frac{a + b}{2} \times h$

حيث

a : طول القاعدة الأولى

b: طول القاعدة الثانية

الآن نحسب مساحة شبه المنحرف كالتالي :

$A = \frac{a + b}{2} \times h$

$= (\frac{2 x + 2}{2}) \times (x - 1)$

$= (\frac{2 x + 2}{2}) \times \frac{x - 1}{1}$

$= \frac{2 (x + 1)}{2} \times \frac{(x - 1)}{1}$

$= x^{2} - 1$

الأن نعوض x=56.

$x^{2} - 1 = 56^{2} - 1 = 3136 - 1 = 3135 c m^{2}$

رياضيات فصل أول

الثامن

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS