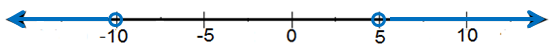حلول أسئلة كتاب الطالب وكتاب التمارين
أسئلة أتحقق من فهمي
أتحقق من فهمي صفحة 18
أكتبُ مُتباينةً مركبةً تمثِّلُ كلَّ جملةٍ ممّا يأتي، ثمَّ أُمَثِّلُها على خطِّ الأعدادِ:
a) عددٌ أكبرُ مِنْ 3- وأقلُّ مِنْ 7
• أختار مُتغيرًا ، ليكن x ممثلًا للعدد
• أكتب المتباينة :
• أمثل المتباينة على خط الأعداد :
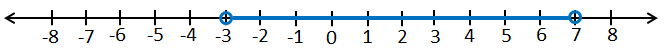
b) عددٌ على الأكثرِ 0 أوْ على الأقلِّ 2
• أختار مُتغيرًا ، ليكن y ممثلًا للعدد
• أكتب المتباينة :
• أمثل المتباينة على خط الأعداد :

أتحقق من فهمي صفحة 20
أكتبُ كلَّ مُتباينةٍ مُرَكَّبَةٍ ممّا يأتي باستعمالِ رمزِ الفترةِ، ثمَّ أُمَثِّلُها على خطِّ الأعدادِ:
a) -10 < x ≤ 10
التعبير برمز الفترة :
التمثيل على خط الأعداد :
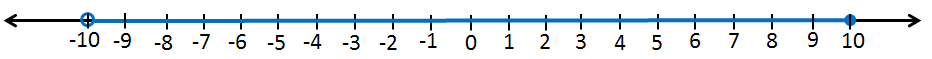
b) x > 1 or x < -4
اتحادُ فترتينِ منفصلتينِ :
التمثيل على خط الأعداد :

c) 7 ≤ x < 12
التعبير برمز الفترة :
التمثيل على خط الأعداد :
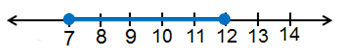
d) x ≤ -8 or x ≥ 8
اتحادُ فترتينِ منفصلتينِ :
التمثيل على خط الأعداد :
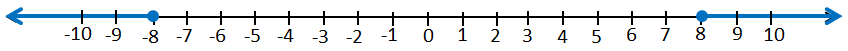
أتحقق من فهمي صفحة 21
أَجِدُ مجموعةَ حلِّ كلِّ مُتباينةٍ ممّا يأتي، ثمَّ أُمَثِّلُها على خطِّ الأعدادِ:
a) -5 < x - 4 < 2
| المُتباينةُ المُعطاةُ | -5 < x - 4 < 2 |
| بجمع 4 إلى كلِّ طَرف | |
| بالتبسيطِ |
مجموعة الحل هي : ، وتُكتب باستخدام رمزِ الفترةِ على الصورةِ : ، ويمكنُ تمثيلُها على خطِّ الأعدادِ علَى النَّحوِ الآتي :
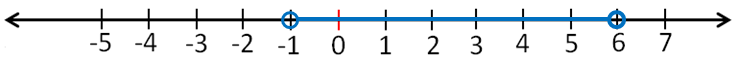
b) -2 < -3x - 8 ≤ 10
| المُتباينةُ المُعطاةُ | -2 < -3x - 8 ≤ 10 |
| بجمع 8 إلى كلِّ طَرف | |
| بقسمة كل طرف على 3- وتغيير اتجاه المتباينة | |
| بالتبسيط | |
| بإعادة كتابة المتباينة |
مجموعة الحل هي : ، وتُكتب باستخدام رمزِ الفترةِ على الصورةِ : ، ويمكنُ تمثيلُها على خطِّ الأعدادِ علَى النَّحوِ :

أتحقق من فهمي صفحة 23
أَجِدُ مجموعةَ حلِّ كلِّ مُتباينةٍ ممّا يأتي، ثمَّ أُمَثِّلُها على خطِّ الأعدادِ:
a) x + 2 ≤ 5 or x - 4 ≥ 2
| المُتباينةُ المُعطاةُ | |
| بحل كل متباينة |
إذنْ، مجموعةُ الحلِّ هيَ : ، ويمكنُ كتابتُها باستعمالِ اتحادِ فترتينِ منفصلتينِ على الصورةِ :
ويمكنُ تمثيلُها على خطِّ الأعدادِ على النَّحوِ الآتي :
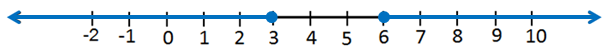
b) -2x + 7 ≤ 13 or 5x + 12 < 37
| المُتباينةُ المُعطاةُ | |
| بحل كل متباينة على حِدة |
|
مجموعة حلِّ المُتباينة هِي اتِّحاد المُتباينتين. إذنْ، أُمَثِّلُ كُلًّ من المُتباينَتينِ الآتِيَتين ، ثمَّ أجِد اتَّحاد التمثيلين :
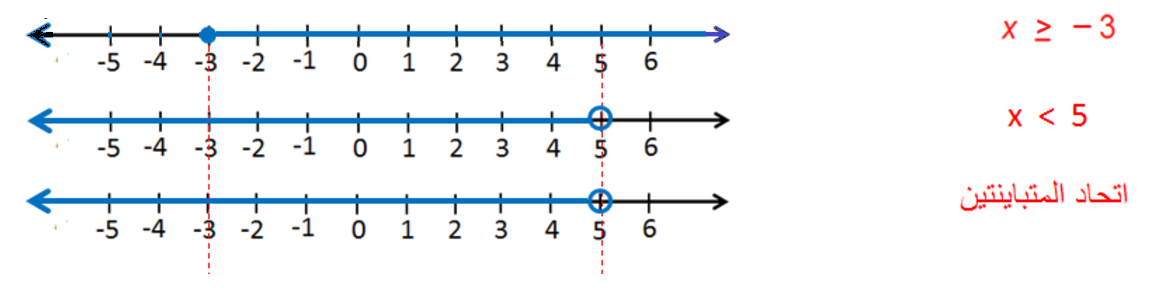
أُلاحظ أنّ التمثيل البيانيّ للمُتباينة x < 5 يحتوي على جميع نقاط التمثيل البيانيّ للمُتباينة x -3 ؛ لِذا يكونُ الاتِّحادُ هُوَ التمثيل البيانيّ للمُتباينة
x < 5 ، وتكون مجموعة الحلِّ : ، ويُمكنُ كتابتُها باستخدام رمز الفترة على الصورة :
أتحقق من فهمي صفحة 24
درجةُ الحرارةِ: إذا عَلِمتُ أنَّ درجةَ حرارةِ الجسمِ الطبيعيَّةَ للأشخاصِ البالغينَ تتراوحُ بينَ ، فأكتبُ مُتباينةً مُرَكَّبَةً تمثِّلُ
درجةَ حرارةِ الشخصِ البالغِ وَأُمَثِّلُها على خطِّ الأعدادِ، ثمَّ أُحَوِّلُ المُتباينةَ إلى الدرجةِ الفهرنهايتيَّةِ. علمًا أنَّ :
الحل :
أختارُ مُتَغَيِّرًا : لِيَكُنْ C مُمَثِّلً لدرجةِ حرارةِ المُحَرِّكِ بالسلسيوس.
أكتبُ المُتباينةَ :
أمثل المتباينة على خط الأعداد :

لِيَكُنْ أنَّ F مُمَثِّلًا لدرجةِ الحرارةِ بالفهرنهايت، وَمِنْهُ :
| المُتباينةُ | |
| بالتعويضِ عن C بـ ( | |
| بضربِ كلِّ طَرَفٍ بـ | |
| بجمعِ 32 لكلِّ طَرَفٍ |
إذنْ، تتراوحُ درجةُ حرارةِ الجسم بينَ
أسئلة أتدرب وأحل المسائل
أكتبُ مُتباينةً مركبةً تمثِّلُ كلَّ جملةٍ ممّا يأتي، ثمَّ أُمَثِّلُها على خطِّ الأعدادِ:
1) عددٌ أكبرُ مِنْ 7- وأقلُّ مِنْ 2
• أكتب المتباينة :
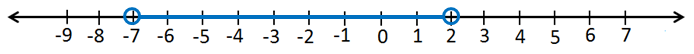
2) عددٌ أقلُّ مِنْ أوْ يُساوي 5- أوْ أكبرُ مِنْ 12
• أكتب المتباينة :
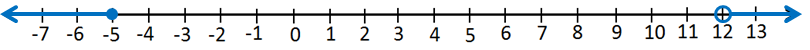
3) عددٌ يقعُ بينَ 10 - وَ 10
• أكتب المتباينة :

4) عددٌ علَى الأكثرِ 2- أوْ على الأقلِّ 9
• أكتب المتباينة :
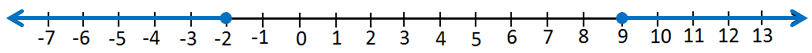
5) ناتج ضرب عدد في 5- أكبرُ مِنْ 35 أوْ أقلُّ مِنْ 10
• أكتب المتباينة :
• أحل المتباينة :
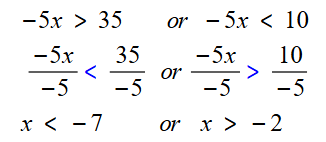
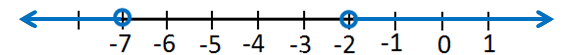
6) عددٌ مطروحٌ منهُ 8 لا يزيدُ على 4 ولا يقلُّ عَنْ 5
• أكتب المتباينة :
• أحل المتباينة :
• أمثل كل متباينة على خط الأعداد ، وألاحظ وجود حرف الواو كأداة ربط بين المتباينتين (لا يزيدُ على 4 و لا يقلُّ عَنْ 5) وعدم وجود نقاط مشتركة يدل على أن مجموعة الحل
أكتبُ كلَّ مُتباينةٍ مُركّبةٍ ممّا يأتي باستعمال رمز الفترة، ثمَّ أُمَثِّلُها على خطِّ الأعدادِ:
7) x ≥ 4 or x ≤ -7
اتحادُ فترتينِ منفصلتينِ :
التمثيل على خط الأعداد :
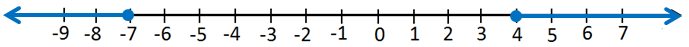
8) -2 < x < 4
التعبير برمز الفترة :
التمثيل على خط الأعداد :
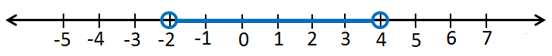
9) x < 2 or x ≥ 15
اتحادُ فترتينِ منفصلتينِ :
التمثيل على خط الأعداد :
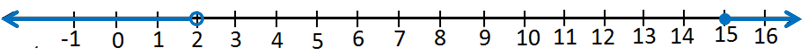
10) -5 ≤ x ≤ 10
التعبير برمز الفترة :
التمثيل على خط الأعداد :

أكتبُ مُتباينةً مُركّبة تُعبّرُ عَن كلِّ تمثيلٍ على خطِّ الأعداد ممّا يأتي، ثمَّ أُعبّرُ عنها برمز الفترة:

الحل :
المتباينة التي تعبر عن التمثيل :
التعبير برمز الفترة :
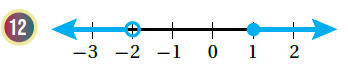
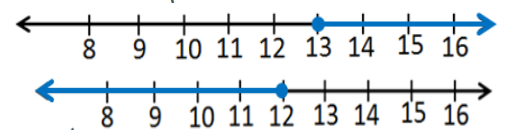
الحل :
المتباينة التي تعبر عن التمثيل :
اتحادُ فترتينِ منفصلتينِ :
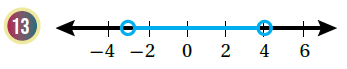
الحل :
المتباينة التي تعبر عن التمثيل :
التعبير برمز الفترة :
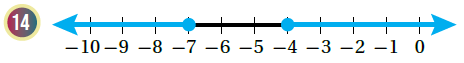
الحل :
المتباينة التي تعبر عن التمثيل :
اتحادُ فترتينِ منفصلتينِ :
أَجِدُ مجموعةَ حلِّ كلِّ مُتباينةٍ ممّا يأتي، ثمَّ أُمَثِّلُها على خطِّ الأعدادِ:
15) -5 < x + 1 < 4
|
|
مجموعة الحل هي :
التمثيل على خط الأعداد :
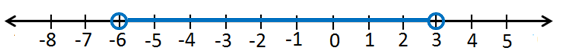
16)
|
|
مجموعة الحل هي :
التمثيل على خط الأعداد :

17) -9 < 3x + 6 ≤ 18
|
|
مجموعة الحل هي :
التمثيل على خط الأعداد :
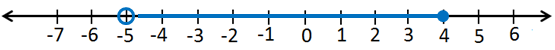
18) x + 1 < -3 or x - 2 > 0
مجموعة الحل هي :
التمثيل على خط الأعداد :
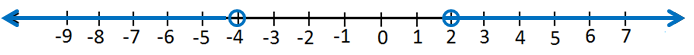
19) 2r + 3 < 7 or -r + 9 ≤ 2
مجموعة الحل هي :
التمثيل على خط الأعداد :
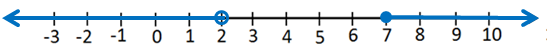
20) 2n + 11 ≤ 13 or -3n ≥ -12
مجموعة حلِّ المُتباينة هِي اتِّحاد المُتباينتين. إذنْ، أُمَثِّلُ كُلًّ من المُتباينَتينِ الآتِيَتين ، ثمَّ أجِد اتَّحاد التمثيلين :
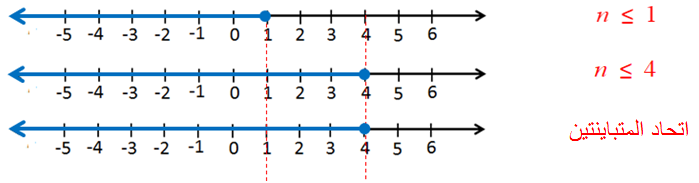
أُلاحظ أنّ التمثيل البيانيّ للمُتباينة يحتوي على جميع نقاط التمثيل البيانيّ للمُتباينة ؛ لِذا يكونُ الاتِّحادُ هُوَ التمثيل البيانيّ للمُتباينة
، وتكون مجموعة الحلِّ : ، ويُمكنُ كتابتُها باستخدام رمز الفترة على الصورة :
21) سُعراتٌ حراريَّةٌ : إذا عَلِمتُ أنَّ حاجةَ الرياضيِّ مِنَ الطاقةِ تعتمدُ على عواملَ عِدَّةٍ، مِنْ أهمِّها كتلتُهُ وسرعةُ التمرينِ، وكانَ رياضيٌّ يحتاجُ يوميًّا ما
بينَ 3000 و 4500 سعرةٍ حراريَّةٍ، فأكتبُ مُتباينةً تمثِّلُ السُّعراتِ الحراريَّةَ الَّتي يحتاجُ إليها الرياضيُّ، وَأُمَثِّلُها على خطِّ الأعدادِ.
الحل :
أفرض أن عدد السعرات الحرارية التي يحتاجها الرياضي x
إذن المتباينة التي تمثل السعرات الحرارية التي يحتاجها الرياضي هي :
التمثيل على خط الأعداد :

مهاراتُ التفكيرِ العُليا
تبريرٌ: إذا كانَ مجموعُ طولَي أيِّ ضلعَيْنِ في المُثَلَّثِ أكبرَ مِنْ طولِ الضِّلعِ الثالثِ، فأستعمِلُ هذه الحقيقةَ للإجابةِ عَنِ السؤالَيْنِ الآتِيَيْنِ تِباعًا:
| 22) هلْ يمكنُ أنْ تكونَ قيمةُ x في المُثَلَّثِ المُجاوِرِ ؟ أُبَرِّرُ إجابتي. | 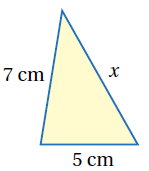 |
الحل :
لا يُمكن ؛ لأنّه إذا جمعنا الضلعين فيجب أن يكون الناتج أكبر من ويمكن كتابة المتباينة على النحو الآتي :
وبحل المتباينة ينتج
23) أستعمِلُ المُثَلَّثَ المُجاوِرَ لكتابةِ مُتباينةٍ تُحَدِّدُ قِيَمَ x المُمكِنَةَ، مُبَرِّرًا إجابتي.
الحل :
إذن المتباينة :
24) أكتشفُ الخطأَ : ناتجُ تقريبِ العددِ x إلى أقربِ 100 هُوَ 400 . تقولُ عبيرُ إنَّ المُتباينةَ تُعَبرُِّ عَنْ جميعِ قِيَمِ x المُحتَمَلَةِ، وتقولُ لمياءُ إنَّ المُتباينةَ تُعَبِّرُ عَنْ جميعِ قِيَمِ x المُحتَمَلَةِ. أيُّهُما إجابتُها صحيحةٌ؟ أُبَرِّرُ إجابتي.
الحل :
إجابة لمياء صحيحة لأن جميع المتباينة تحتوي على جميع قيم x المحتملة (عند تقريبهم لأقرب 100 فإن ناتج التقريب يساوي 400) ، بينما إجابة عبير لا تعبر عن جميع قيم x المحتملة.
تبريرٌ : أَجِدُ مجموعةَ حلِّ كلِّ مُتباينةٍ ممّا يأتي، مُبَرِّرًا إجابتي:
الحل :
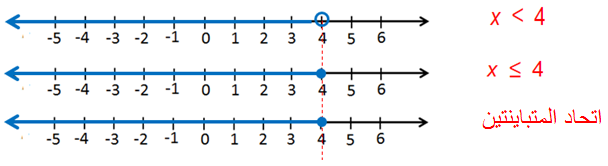
25) -1 + x < 3 or - x ≥ - 4
وجود or يكون الحل باتحاد الحلين (الفتريتين) ، إذن مجموعة الحل :
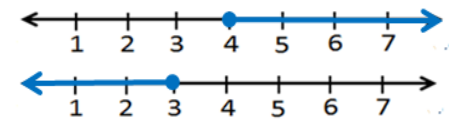
26) 3x - 7 ≥ 5 and 2x + 6 ≤ 12
وجود and يكون الحل بتقاطع الحلين (الفتريتين) ، إذن مجموعة الحل:
أسئلة كتاب التمارين
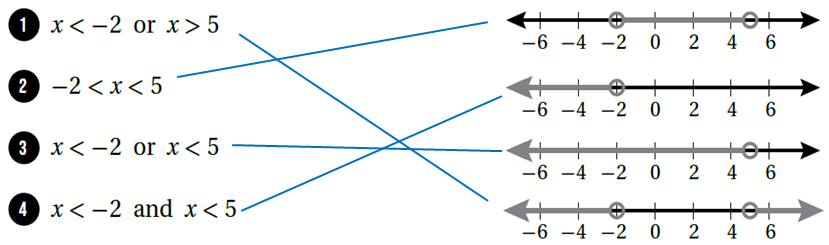
أَصِلُ المُتباينةَ بتمثيلِها على خطِّ الأعدادِ في كلٍّ ممّا يأتي:
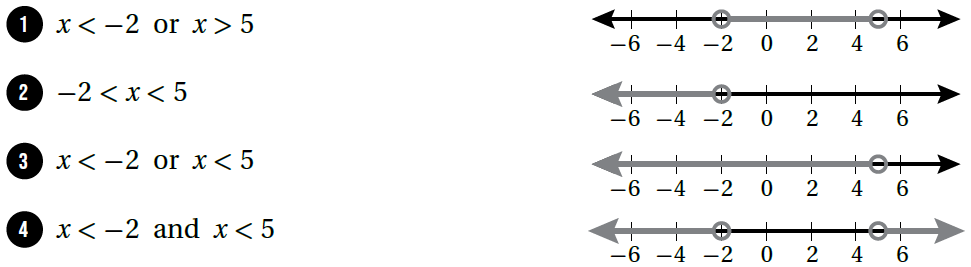
الحل :
أكتبُ مُتباينةً تمثِّلُ كلَّ جملةٍ ممّا يأتي، ثمَّ أُمَثِّلُها على خطِّ الأعدادِ:
|
5) عددٌ يقعُ بينَ 5- و 7 |
 |
الحل :
5) عددٌ يقعُ بينَ 5- و 7
المتباينة :

6) ناتجُ 4 معَ ثلاثةِ أمثالِ عددٍ يقعُ بينَ 8- و 10
المتباينة :

7) نصفُ عددٍ أكبرُ مِنْ 0 وأقلُّ مِنْ أوْ يُساوي 1
المتباينة :

8) عددٌ على الأقلِّ 2 وعلى الأكثرِ 9
المتباينة :
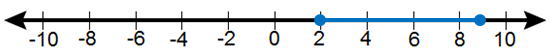
أَجدُ مجموعةَ حلِّ كلِّ مُتباينةٍ ممّا يأتي ، ثمَّ أُمثّلها على خطِّ الأعداد :
الحل :
9) 3b - 1 < 7 or 4b + 1 > 9
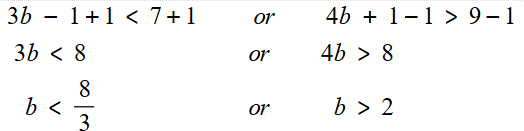
مجموعة الحل :

10) 4 + k > 3 or 6k < -30
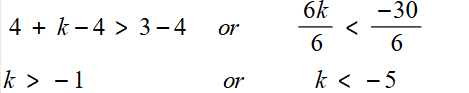
مجموعة الحل :
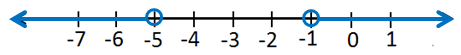
11) 7 - 3c ≥ 1 or 5c + 2 ≥ 17
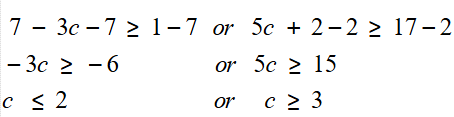
مجموعةُ حلِّ المُتباينةِ هِيَ اتِّحادُ المُتباينَتَيْنِ :
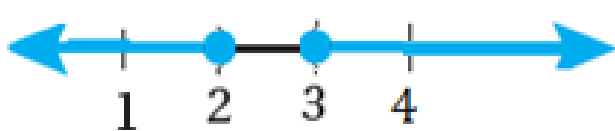
12) 6 - a < 1 or 3a ≤ 12
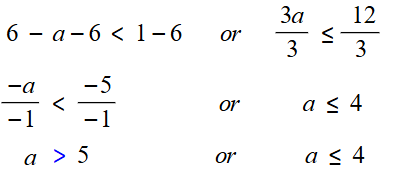
مجموعة الحل :

13) 7 ≤ 3 - 2p < 11
مجموعة الحل:

14) 1.5 < w + 3 < 6.5
مجموعة الحل :
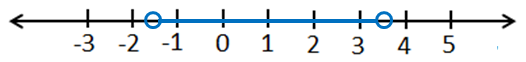
15) -6 ≤ 3x + 9 < 21
مجموعة الحل:

16) -9 < -2s -1 ≤ -7
مجموعة الحل :

17) أكتشفُ الخطأَ: أكتشفُ الخطأَ في حلِّ المُتباينة المُركَّبة الآتية، وأُصحِّحُهُ:
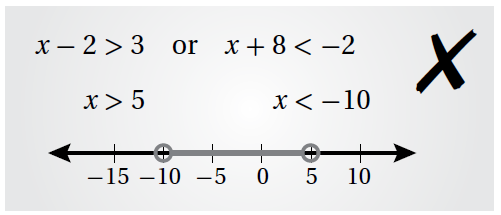
الحل :
الخطأ في حل المتباينة في تحديد فترتي الحل ، والحل الصحيح :
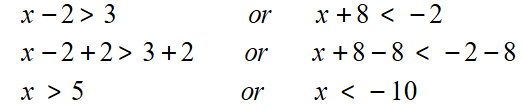
اتحادُ فترتينِ منفصلتينِ :