حلُّ المُعادلاتِ التربيعيَّةِ بإكمالِ المُرَبَّعِ

Solving Quadratic Equations
by Completing the Square

فكرة الدرس : حلُّ المُعادلات التربيعيَّة بإكمال المُربَّع.

أولًا : إكمال المُرَبّع

يمكنُ تحويلُ المقدارِ التربيعيِّ الذي على الصورةِ x² + bx إلى مُرَبَّعٍ كاملٍ ثُلاثِيِّ الحدودِ بإضافةِ ${\left(\frac{b}{2}\right)}^2$ ، وَتُسَمّى هذهِ العمليَّةُ إكمالَ المُرَبَّعِ

مفهومٌ أساسيٌّ (إكمالُ المُرَبَّعِ)

بالكلمات : لإكمالِ مُرَبَّع أيِّ مقدارٍ تربيعيٍّ على الصورة x2 + bx ، أتَّبعُ الخُطوات الآتية : الخُطوة 1 : أَجِدُ نصف b. الخُطوة 2 : أُرَبِّعُ الناتجَ من الخُطوة 1 الخُطوة 3 : أُضيفُ الناتجَ مِنَ الخُطوة 2 إلى  x2 + bx بالرُّموز  : $x^2+bx + {\left(\frac{b}{2}\right)}^2={\left( x + \frac{b}{2}\right)}^2$

 

 

 

 

 

 

 

 

•• أتعلَّمُ : أتَّبِعُ الخُطواتِ نفسَها، سواءٌ كانتْ b موجبةً أوْ سالبةً.

 

 

مثال : 

أجعل كلَّ مقدار مما يأتي مُربعًا كاملًا ، ثمّ أُحلّلُ المُرَبع الكامل ثُلاثيّ الحدود الناتج :

$\mathit{a}\mathbf{)} x^2+8x \mathbf{ }\mathbf{ }\mathit{b}\mathbf{)} x^2-14x$

الحل : 

$\mathit{a}\mathbf{)} x^2+8x$

بإيجاد  $\frac{b}{2}$	$\frac{8}{2}=4$
بإيجاد ${\left(\frac{b}{2}\right)}^2$	$4^2= 16$
بإضافة ${\left(\frac{b}{2}\right)}^2$ إلى المقدار الأصلي	$x^2+8x +16$

 

 

 

 

 

إذنْ، المقدارُ الناتجُ بعدَ إكمالِ المُرَبَّعِ هُوَ x² + 8x + 16 ، ويمكنُ تحليلُهُ كما يأتي :

بتحليلِ المُرَبَّعِ الكاملِ ثُلاثِيِّ الحدودِ  ²(x² + 8x + 16 = (x + 4

---

 

$\mathit{b}\mathbf{)} x^2-14x$

بإيجاد ${\frac{b}{2} }^{ }$	$-\frac{14}{2}=-7$
بإيجاد ${\left(\frac{b}{2}\right)}^2$	${(-7)}^2= 49$
بإضافة  ${\left(\frac{b}{2}\right)}^2$    إلى المقدار الأصلي	$x^2-14x+49$

 

 

 

 

 

إذنْ، المقدارُ الناتجُ بعدَ إكمالِ المُرَبَّعِ هُوَ x² - 14x + 49 ، ويمكنُ تحليلُهُ كما يأتي :

بتحليلِ المُرَبَّعِ الكاملِ ثُلاثِيِّ الحدودِ ²(x² - 14x + 49 = (x - 7

---

 

ثانيًا : حلُّ المُعادلات التربيعيَّة علَى الصورة x² + bx + c = 0 بإكمال المُرَبَّع 

يُمكِنُني استعمالُ إكمالِ المُرَبَّعِ لحلِّ أيِّ مُعادلةٍ تربيعيَّةٍ على الصورةِ ، x² + bx + c = 0 وذلكَ يتطلَّبُ فصلَ المقدارِ x² + bx في الطرفِ الأيسرِ أوَّلًا ،

ثمَّ أُكمِلُ المُرَبَّعَ.

مثال : 

أَحلُّ كُلًّ من المُعادلات الآتية بإكمال المُرَبّع، مُقَرِّبًا إجابتي لأقرب جزء مِنْ عشرَة (إن لَزِم) :

a) x² + 6x - 7 = 0                                                                         b) x² - 5x + 2 = 0

الحل : 

a) x² + 6x - 7 = 0

المُعادلة المُعطاة	x2 + 6x - 7 = 0
بجمع 7 إلى طرفي المُعادلة	x2 + 6x = 7
بإكمال المُرَبع بإضافة${\left(\frac{6}{2}\right)}^2 = 9$ إلى طرفي المُعادلة	x2 + 6x + 9 = 7 + 9
بتحليل المُربّع الكامل ثُلاثِيِّ الحدود	${(x + 3)}^2 = 16$
بأخذ الجذر التربيعيّ للطرفَيْن	$x + 3 = \pm 4$
بطرحِ 3 مِن طرفي المُعادلة	$x =-3\pm 4$
بفصلِ الحلَّيْن	$x = -3 + 4 or x = -3-4$
بالتبسيط	$x = 1 or x = -7$

 

 

 

 

 

 

 

 

 

إذن ، جذرا المُعادلة  7- , 1

للتحقّق، أُعَوّض قيمتَي x في المُعادلة الأصليَّة.

---

b) x² - 5x + 2 = 0

المُعادلة المُعطاة	x2 - 5x + 2 = 0
بطرح 2 من طرفي المُعادلةِ	x2 - 5x  = - 2
بإكمال المُربع بإضافة ${(-\frac{5}{2})}^2 = \frac{25}{4}$ إلى طرفي المُعادلة	$x^2 - 5x+ \frac{25}{4} = - 2+\frac{25}{4}$
بتحليلِ المُرَبَّعِ الكاملِ ثُلاثِيِّ الحدودِ	${\left( x - \frac{5}{2}\right)}^2 = \frac{17}{4}$
بأخذ الجذر التربيعيّ للطرفَيْن	$x - \frac{5}{2} =\pm \frac{\sqrt{17}}{2}$
بجمع $\frac{5}{2}$ إلى طرفي المُعادلة	$x = \frac{5}{2}\pm \frac{\sqrt{17}}{2}$
بفصلِ الحلَّيْن	$x = \frac{5}{2}+\frac{\sqrt{17}}{2} or x = \frac{5}{2}-\frac{\sqrt{17}}{2}$
باستخدام الآلة الحاسبة	$x \approx 4.6 or x \approx 0.4$

 

 

 

 

 

 

 

 

 

 

 

إذن ، جذرا المُعادلة التقريبيان هما   0.4 , 4.6

---

 

ثانيًا : حلُّ المُعادلاتِ التربيعيَّةِ على الصورةِ ax² + bx + c = 0 بإكمالِ المُرَبَّعِ.

لحلِّ المُعادلةِ التربيعيَّةِ على الصورةِ ax² + bx + c = 0 ؛ حيثُ a ≠ 1 ، أقسِمُ كلَّ حدٍّ في المُعادلةِ على a ، ثمَّ أفصِلُ الحدَّيْنِ اللذَيْنِ يحتويانِ على x² و x في الطرفِ الأيسرِ أوَّلًا ، ثمَّ أُكمِلُ المُرَبَّعَ.

مثال : 

أَحلُّ كُلٍّ من المُعادلات الآتية بإكمال المُرَبَّع :

a) 2x² + 12x - 4 = 0                                                        b) 4x² + 8x + 6 = 0           

الحل : 

المُعادلة المُعطاة	2x2 + 12x - 4 = 0
بقسمة المعادلة على 2	x2 + 6x - 2 = 0
بجمع 2 إلى طرفي المُعادلةِ	x2 + 6x  = 2
بإكمال المُربع بإضافة ${\left(\frac{6}{2}\right)}^2 = 9$ إلى طرفي المُعادلة	x2 + 6x + 9  = 2 +9
بتحليلِ المُرَبَّعِ الكاملِ ثُلاثِيِّ الحدودِ	${(x+3)}^2 = 11$
بأخذ الجذر التربيعيّ للطرفَيْن	$x + 3 = \pm \sqrt{11}$
بطرح 3 من طرفي المعادلة	$x = -3 \pm \sqrt{11}$
بفصلِ الحلَّيْن	$x = -3 + \sqrt{11} or x =-3 - \sqrt{11}$

 

 

 

 

 

 

 

 

 

إذن ، جذرا المُعادلة $x=-3+\sqrt{11} , x=-3-\sqrt{11}$

---

b) 4x² + 8x + 8 = 0 

المُعادلة المُعطاة	4x2 + 8x + 8 = 0
بقسمة المعادلة على 4	x2 + 2x + 2 = 0
بطرح 2 من طرفي المُعادلةِ	x2 + 2x = - 2
بإكمال المُربع بإضافة ${\left(\frac{2}{2}\right)}^2 = 1$ إلى طرفي المُعادلة	x2 + 2x + 1 = - 2 + 1
بتحليلِ المُرَبَّعِ الكاملِ ثُلاثِيِّ الحدودِ	${(x +1)}^2 = -1$

 

 

 

 

 

 

بما أنَّهُ لا توجدُ أعدادٌ حقيقيَّةٌ مُرَبَّعاتُها سالبةٌ فالمُعادلةُ ليسَ لها حُلولٌ حقيقيَّةٌ.

---

 

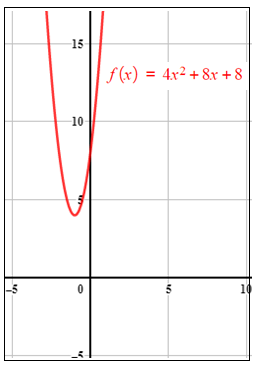•• الدَّعمُ البيانيُّ يظهرُ في الشكلِ المجاور منحنى الاقترانِ التربيعيِّ المُرتبطِ بالمُعادلةِ 0= 3x2+6x+15 ، الذي لا يقطعُ المحورَ x ؛ ما يعني عدمَ وجودِ حُلولٍ حقيقيَّةٍ للمُعادلةِ.