حلول أسئلة كتاب الطالب وكتاب التمارين
أسئلة أتحقق من فهمي
أتحقق من فهمي صفحة 27
أَجِدُ قيمة كلٍّ من المقادير الجبرية الآتية عند القيمة المُعطاة:
a) |x - 2| + 10, x = - 4
b) -2 |3x + 1|, x = -1
الحل :
a) |x - 2| + 10 , x = - 4
| - 4 - 2 | + 10 = | -6 | + 10 = 6 + 10 = 16
b) -2 |3x + 1| , x = -1
-2 |3(-1) + 1 | = -2 | -3 + 1 | = -2 | -2 | = -2 (2) = - 4
أتحقق من فهمي صفحة 29
أَحُلّ كُلًّ من المُعادلات الآتية ، وأُمثّل مجموعةَ الحلِّ على خطِّ الأعداد (إنْ أمكن) :
a) | x - 7| = 5
| بكتابة المُعادلتين المُرتبطتين | x - 7 = 5 or x - 7 = - 5 |
| بجمع 7 لكلّ طرف | x = 12 or x = 2 |
مجموعةُ حلِّ المُعادلةِ هِيَ: { 12 , 2}
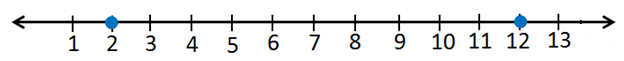
b) 4|2x + 7| = 16
| بقسمة الطرفين على 4 | |2x + 7| = 4 |
| بكتابة المُعادلتين المُرتبطتين | 2x + 7 = 4 or 2x + 7 = - 4 |
| بطرح 7 من كل طرف | 2x = -3 or 2x = - 11 |
| بقسمة كل طرف على 2 | x = - 1.5 or x = -5.5 |
مجموعةُ حلِّ المُعادلةِ هِيَ: { 1.5- , 5.5-}
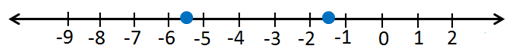
c) |x + 4| = -10
المُعادلةُ 10 - = |x + 4| تعني أنَّ المسافةَ بينَ x و 4- تُساوي 10 -
وبما أنّه لا يمكنُ أنْ تكونَ المسافة سالبة ؛ فإنَّ مجموعةَ حلِّ هذهِ المُعادلةِ ∅ ؛ أيْ أنّه لا يوجدُ حلٌّ للمعادلةِ.
أتحقق من فهمي صفحة 30
أَحُلُّ كُلًّ من المُتبايناتِ الآتيةِ، وأُمثِّل مجموعة الحلِّ على خطِّ الأعداد (إن أمكن) :
a) |x - 2| ≤ 1
| المُتباينة المُركّبة المُرتبطة | |
| بجمع 2 إلى كل طرف |
إذنْ، مجموعةُ حلِّ المُتباينةِ هيَ ، ويمكنُ كتابتُها باستعمالِ رمزِ الفترةِ على الصورةِ: [3 ، 1] ، وَيمكنُ تَمثيلُها على خطِّ الأعدادِ على النَّحوِ الآتي:

b) |x + 7| + 10 < 2
|x + 7| + 10 - 10 < 2 - 10
|x + 7| < - 8
بِما أنَّ | x + 7 | لا يمكنُ أنْ تكونَ سالبةً، فلا يمكنُ أنْ تكونَ | x + 7 | أقلَّ مِنْ 8 - ، وَمِنْهُ فإنَّ مجموعةَ حلِّ هذهِ المُتباينةِ ∅ ؛ أيْ أنّه لا يوجدُ حلٌّ للمتباينةِ المُعطاةِ.
أتحقق من فهمي صفحة 32
أَحُلُّ كُلًّ من المُتبايناتِ الآتيةِ، وأُمثِّل مجموعة الحلِّ على خطِّ الأعداد (إن أمكن) :
| المُتباينة المُرَكّبة المُرتبطة | |
| بجمع 3 إلى كُلِّ طرف |
إذنْ مجموعةُ الحلِّ هي : ، ويمكنُ كتابتُها باستعمالِ اتحادِ فترتينِ منفصلتينِ على الصورةِ :
وتمثيلها البياني على النحو الآتي :
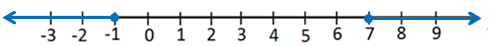
يَنُصُّ تعريفُ القيمةِ المُطلقةِ على أنَّ مقدارَها يجبُ أنْ يكونَ أكبرَ مِنْ أوْ يُساوي صِفرًا ، وَمِنْهُ فإنَّ دائمًا أكبرُ مِنْ لأيٍّ مِنْ قِيَمِ
المُتَغَيِّرِ x .
إذنْ ، مجموعةُ الحلِّ هِيَ مجموعةُ الأعدادِ الحقيقيَّةِ R، ويمكنُ كتابتُها باستعمالِ رمزِ الفترةِ على الصورةِ :
أتحقق من فهمي صفحة 33
صناعةٌ: إذا عَلمت أنَّ طول القُطر المثاليَّ لأحد المكابس الأُسطوانيَّة في مُحَرِّكات السيّارات 90 mm ، وَيُسمَحُ أنْ يزيد طولُ هذا القُطر أوْ يقلَّ بمقدارٍ لا يتجاوزُ ، فأكتبُ مُتباينةَ قيمةٍ مُطلقةٍ أَجِدُ بِها المدى المسموح به لطول قُطر المكبس.
الحل :
بالكلماتِ : الفرقُ بينَ طولِ القطر الحقيقيِّ وطولِ القطر المثاليِّ لا يتجاوزُ
أختار مُتغيرًا : ليكن x مُمثّلًا طول القطر.
أكتبُ المُتباينة :
أحل المتباينة :
بالتبسيط :
إذن ، المدى المسموحُ به لطول المسمار هو بوحدة mm.
أسئلة أتدرب وأحل المسائل
أَجِدُ قيمة كلٍّ من المقادير الجبرية الآتية عند القيمة المُعطاة:
أَحُلّ كُلًّ من المُعادلات الآتية ، وأُمثّل مجموعةَ الحلِّ على خطِّ الأعداد (إنْ أمكن) :





بقسمة الطرفين على
القيمة المطلقة تمثل مسافة وبِما أنَّهُ لا يمكنُ أنْ تكونَ المسافةُ سالبةً فإنَّ مجموعةَ حلِّ هذهِ المُعادلةِ ∅ ؛ أيْ أنّه لا يوجدُ حلٌّ للمعادلةِ.
أَحُلّ كُلًّ من المُتباينات الآتية ، وأُمثّل مجموعةَ الحلِّ على خطِّ الأعداد (إنْ أمكن) :



يَنصّ تعريف القيمة المُطلقة على أنّ مقدارها يجب أن يكون أكبر من أو يُساوي صفرًا ، ومنهُ فإنّ | 3x - 1 | دائمًا أكبر من 6 - لأيٍّ من قيم المتغير x
إذن : مجموعة الحل هي مجموعة الأعداد الحقيقية R، ويمكن كتابتها باستعمال رمز الفترة على الصورة :


بما أنَّ لا يمكن أن تكون سالبة، فلا يمكن أن تكون أقل من 4 -، ومنه فإنَّ مجموعة حلِّ هذه المُتباينة ∅ ؛ أي أنّه لا يوجد حل للمتباينة المُعطاة.

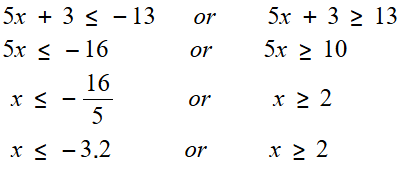

أكتب مُعادلة قيمة مُطلقة تُعبر عن كُلِّ تمثيلٍ على خطِّ الأعداد ممّا يأتي :
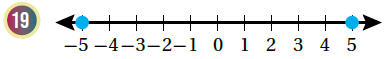
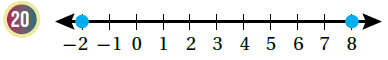
أكتب مُتباينة تمثِّل كلَّ جملةٍ ممّا يأتي، ثمَّ أُمثلها على خطِّ الأعداد :
21) المسافة بين عددٍ والصِّفر أكبر من 7
الحل :
أفرض أنّ العدد x ، البعد بين x و الصفر أكبر من 7 ، إذن المتباينة :

22) المسافة بين عددٍ و 3 أقلُّ من أو تُساوي 4
الحل :
أفرض أنّ العدد x ، البعد بين x و 3 أقل من أو يساوي 4 ، إذن المتباينة :

23) صناعةٌ: إذا عَلِمتُ أنَّ مصنعًا يُنتِجُ علبَ بسكويتٍ كتلتُها المثاليَّةُ ، وكانَ مراقبُ الجودة يستثني العلب التي تزيد على الكتلة المثالية أو
تنقُص عنها بمقدار ، فأكتبُ مُتباينة قيمة مُطلقة أَجد بها المدى المسموح به لِكُتل علب البسكويت.
الحل :
بالكلماتِ : الفرقُ بين الكتلة الحقيقية والكتلة المثالية لا يتجاوز
أختار مُتغيرًا : ليكن x مُمثّلًا للكتلة.
أكتبُ المُتباينة :
أحل المتباينة :
إذن ، المدى المسموحُ به لكتل علب البسكويت هو بوحدة g.
24) كرةُ قَدَم : إذا كانت الكتلة المثالية المُوصى بها لكرة القدم ، وكان مسموحًا أنْ تزيد على الكتلةِ المثالية أوْ تنقُص عنها بمقدار ، فأكتب مُعادلة قيمة مُطلقة لإيجاد أكبر وأقلِّ كتلة مسموح بها لكرة القدم ، ثمّ أحلُّها.
الحل :
بالكلماتِ : الفرق بين الكتلة الحقيقية والكتلة المثالية لا يتجاوز
أختار مُتغيرًا : ليكن x مُمثّلًا للكتلة.
أكتبُ المُعادلة :
أحل المعادلة :
إذن أكبر كتلة مسموح بها هي ، وأقل كتلة مسموح بها هي :
مهاراتُ التفكيرِ العُليا
تبريرٌ : أكتبُ مُتباينة قيمة مُطلقة تُعبِّر عن كُلِّ تمثيلٍ على خطِّ الأعداد ممّا يأتي ، مُبرّرًا إجابتي :
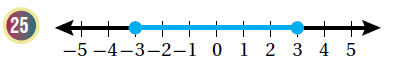
الحل :
أفرض أن العدد هو x
المتباينة :
التبرير : العدد صفر في منتصف المسافة ، إذن البعد عن الصفر ، منطقة الحل محصورة العددين 3 ، 3- بما في ذلك العددين
المسافة بين الحد الأعلى إلى الصفر أو الحد الأدنى إلى الصفر تساوي 3 وحدات ، إذن المتباينة هي :

الحل :
أفرض أن العدد هو x
المتباينة :
التبرير : العدد 1 في منتصف المسافة ، إذن البعد عن 1 ، منطقة الحل محصورة العددين 3 ، 1- باستثناء العددين
المسافة بين الحد الأعلى إلى 1 ، أو الحد الأدنى إلى 1 تساوي 2 وحدة ، إذن المتباينة هي :
|
27) تبريرٌ: يُبَيِّنُ الشكلُ المجاوِرُ مُثَلَّثًا ومُستطيلً الفرقُ بين مساحتيهما أقلُّ من 2 وحدةٍ مُرَبَّعَةٍ. أكتبُ مُتباينة قيمة مُطلقة تمثّلُ الجملة السابقة وأَحُلُّها، مُبَرِّرًا إجابتي. |
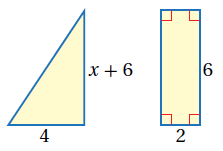 |
الحل :
مساحة المستطيل :
مساحة المثلث :
الفرق بين مساحتيهما أقل من 2 :
أحل المتباينة :
|
|
28) تَحَدٍّ: أَحُلُّ المُتباينةَ المُرَكَّبَةَ الآتيةَ :
الحل :
|
|
مجموعة الحل هي الفترة المشتركة بين المتباينتين :
أسئلة كتاب التمارين
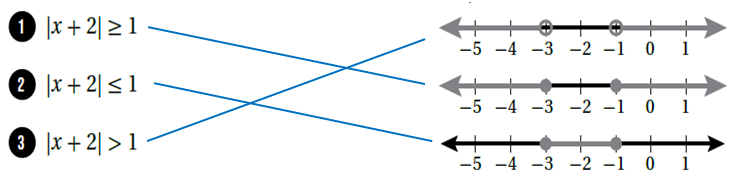
أَصِلُ المُتباينةَ بتمثيلِها على خطِّ الأعدادِ في كلٍّ ممّا يأتي:
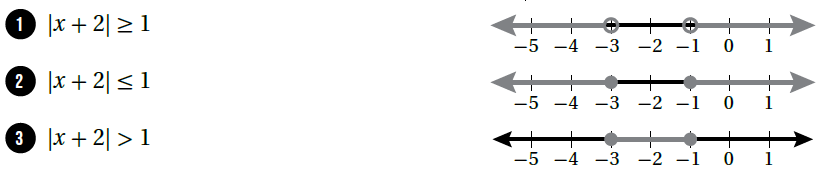
الحل :
أكتبُ مُتباينةً تمثِّلُ كلَّ جملةٍ ممّا يأتي، ثمَّ أُمَثِّلُها على خطِّ الأعدادِ :
4) المسافةُ بينَ عددٍ و 2 على الأكثرِ 13
الحل :
أفرض أن العدد هو x
المتباينة :
أحل المتباينة :

5) المسافةُ بينَ عددٍ والصِّفرِ على الأقلِّ 6
الحل :
أفرض أن العدد هو x
المتباينة :
أحل المتباينة :

6) أُصَنِّفُ المُعادلاتِ أدناهُ دونَ حَلِّها إلى واحدةٍ مِنَ الفئاتِ الآتيةِ : لها حلان ، لها حل واحد ، ليس لها حل .
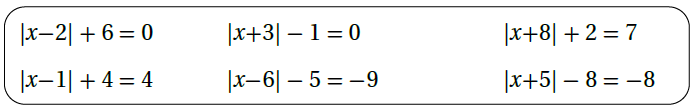
الحل :
| عدد الحلول | المعادلة |
| ليس لها حل | x - 2 | + 6 = 0 | |
| لها حلان | x - 3 | - 1 = 0 | |
| لها حلان | x + 8 | + 2 = 7 | |
| لها حل واحد | x - 1 | + 4 = 4 | |
| ليس لها حل | x - 6 | - 5 = - 9 | |
| لها حل واحد | x + 5 | - 8 = - 8 | |
أَحُلُّ كلًّ مِنَ المُعادلاتِ والمُتبايناتِ الآتيةِ :
مجموعة الحل :
مجموعة الحل :
مجموعة الحل :
مجموعة الحل :
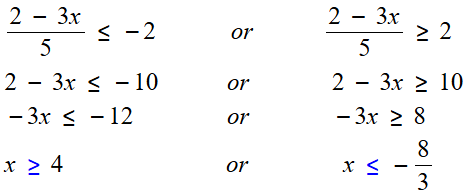
مجموعة الحل :
مجموعة الحل :
13) أكتشفُ الخطأ : أكتشفُ الخطأَ في حلِّ مُعادلةِ القيمةِ المُطلقةِ الآتيةِ، وأُصحِّحُهُ :
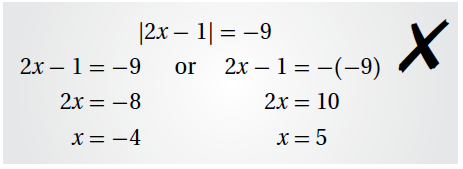
الحل :
القيمة المطلقة لا تساوي عدد سالب لأنها تمثل مسافة ؛ والحل الصحيح لا يوجد حل لهذه المعادلة.