رياضيات فصل ثاني

  $\mathbf{تدريب}\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{ }\mathbf{٧}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{١٤}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{صفحة}\mathbf{ }\mathbf{٩٧}$

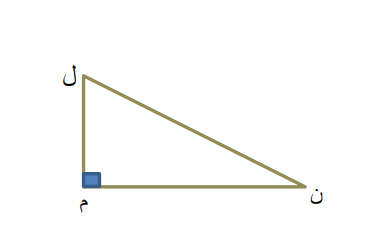
 حل المثلث  ل م ن القائم الزاوية في م ، الذي فيه :  $\mathbf{ }\mathit{ل}\mathbf{ }\mathit{م}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٦}\mathbf{ }\mathbf{سم}\mathbf{ }\mathbf{،}\mathbf{ }\mathit{م}\mathbf{ }\mathit{ن}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٢}\mathbf{ }\mathbf{سم}\mathbf{ }$؟

       

       $$\begin{gathered} \mathbf{بتطبيق}\mathbf{ }\mathbf{مبرهنة}\mathbf{ }\mathbf{فيثاغورس}\mathbf{ }\mathbf{نجد}\mathbf{ }\mathbf{طول}\mathbf{ }\mathbf{الضلع}\mathbf{ }\mathbf{ }\mathit{ل}\mathbf{ }\mathit{م}\mathbf{ } \\ \mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{ل}\mathbf{ }\mathit{م}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{=}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{١٦}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{١٢}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{٢٥٦}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{ }\mathbf{١٤٤} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{٤٠٠}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ل}\mathbf{ }\mathit{م}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{٢٠}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ظا}\mathbf{ }\mathit{ل}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{١٢}}{\mathbf{١٦}}\mathbf{=}\mathbf{ }\mathbf{٧٥}\mathbf{,}\mathbf{٠}\mathbf{ }\mathbf{ }\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{باستخدام}\mathbf{ }\mathbf{الالة}\mathbf{ }\mathbf{الحاسبة}\mathbf{ }\mathbf{ }\mathbf{نجد}\mathbf{ }\mathbf{ }\mathbf{\angle }\mathbf{ }\mathit{ل}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣٧}\mathbf{°} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{\angle }\mathbf{ }\mathbf{ }\mathit{م}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{٥٣}\mathbf{°} \end{gathered}$$

 

$\mathbf{تدريب}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٧}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{١٥}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{صفحة}\mathbf{ }\mathbf{ }\mathbf{٩٩}$

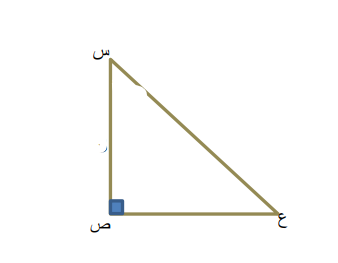
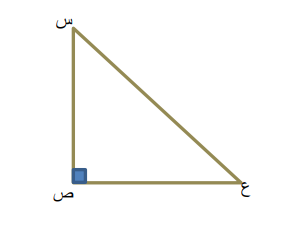
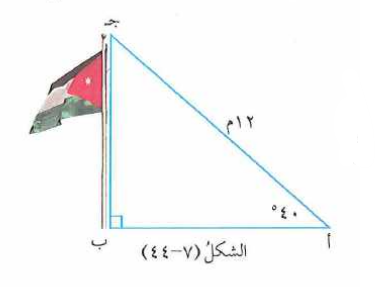
   حل المثلث س ص ع القائم الزاوية في ص ، الذي فيه :  $\mathit{س}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٧}\mathbf{ }\mathbf{سم}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{ظا}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١}\mathbf{ }$ ؟           

          $$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{ظا}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{ع}\mathbf{ }\mathbf{ص}\mathbf{ }}{\mathbf{٧}\mathbf{ }} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\frac{\mathbf{ع}\mathbf{ }\mathbf{ص}\mathbf{ }}{\mathbf{ }\mathbf{٧}\mathbf{ }}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathit{ع}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٧}\mathbf{ }\mathbf{سم}\mathbf{ } \\ \mathbf{بتطبيق}\mathbf{ }\mathbf{مبرهنة}\mathbf{ }\mathbf{فيثاغورس}\mathbf{ }\mathbf{نجد}\mathbf{ }\mathbf{(}\mathbf{ }\mathit{ع}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{)}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{ع}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{٧}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{٧}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{٤٩}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{ }\mathbf{٤٩}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{٩٨}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ع}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{ }\sqrt{\mathbf{٩٨}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ظا}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathit{س}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٤٥}\mathbf{°}\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{ }\mathit{ع}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٤٥}\mathbf{°} \end{gathered}$$

 

 

$\mathbf{تدريب}\mathbf{ }\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٧}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{١٦}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{صفحة}\mathbf{ }\mathbf{ }\mathbf{١٠٠}$

 

    وقف بشار عند النقطة ( أ ) التي تبعد  $\left(\mathrm{١٢}\right)$ مترًا عن قمة سارية علم المدرسة ، فإذا كان قياس الزاوية ( أ ) يساوي  $\mathbf{٤٠}\mathbf{°}$ كما في الشكل  $\left(\mathrm{٧} -\mathrm{٤٤}\right)$ فجد : 

           $$\begin{gathered} \mathbf{١}\mathbf{)}\mathbf{ }\mathbf{قياس}\mathbf{ }\mathbf{الزاوية}\mathbf{ }\mathbf{(}\mathbf{ }\mathit{ج}\mathbf{ }\mathbf{)}\mathbf{ } \\ \mathbf{٢}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{المسافة}\mathbf{ }\mathbf{بين}\mathbf{ }\mathbf{النقطة}\mathbf{ }\mathbf{(}\mathbf{ }\mathit{أ}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{التي}\mathbf{ }\mathbf{يقف}\mathbf{ }\mathbf{عندها}\mathbf{ }\mathbf{بشار}\mathbf{ }\mathit{و}\mathbf{ }\mathbf{قاعدة}\mathbf{ }\mathbf{السارية}\mathbf{ } \\ \mathbf{٣}\mathbf{)}\mathbf{ }\mathbf{ارتفاع}\mathbf{ }\mathbf{السارية}\mathbf{ } \end{gathered}$$                      

 

 

 

           $$\begin{gathered} \mathbf{١}\mathbf{)}\mathbf{ }\mathbf{قياس}\mathbf{ }\mathbf{الزاوية}\mathbf{ }\mathbf{(}\mathbf{ }\mathit{ج}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩٠}\mathbf{°}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٤٠}\mathbf{°}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٥٠}\mathbf{°} \\ \mathbf{٢}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{المسافة}\mathbf{ }\mathbf{بين}\mathbf{ }\mathbf{النقطة}\mathbf{ }\mathbf{(}\mathbf{ }\mathit{أ}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{التي}\mathbf{ }\mathbf{يقف}\mathbf{ }\mathbf{عندها}\mathbf{ }\mathbf{بشار}\mathbf{ }\mathbf{،}\mathbf{ }\mathit{و}\mathbf{ }\mathbf{قاعدة}\mathbf{ }\mathbf{السارية}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathit{أ}\mathbf{ }\mathit{ب}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{جتا}\mathbf{ }\mathbf{٤٠}\mathbf{°}\mathbf{=}\mathbf{ }\frac{\mathbf{أ}\mathbf{ }\mathbf{ب}\mathbf{ }}{\mathbf{١٢}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{٧٦٦}\mathbf{,}\mathbf{٠}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{أ}\mathbf{ }\mathbf{ب}\mathbf{ }}{\mathbf{١٢}}\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathit{أ}\mathbf{ }\mathit{ب}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٩}\mathbf{,}\mathbf{٩}\mathbf{ }\mathit{م}\mathbf{ } \\ \mathbf{٣}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ارتفاع}\mathbf{ }\mathbf{السارية}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathit{ب}\mathbf{ }\mathit{ج}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{جا}\mathbf{ }\mathbf{٤٠}\mathbf{°}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{ }\mathbf{ب}\mathbf{ }\mathbf{ج}\mathbf{ }}{\mathbf{١٢}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{٦٤٢٨}\mathbf{,}\mathbf{٠}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{ب}\mathbf{ }\mathbf{ج}\mathbf{ }}{\mathbf{١٢}}\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathit{ب}\mathbf{ }\mathit{ج}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٧١}\mathbf{,}\mathbf{٧}\mathbf{ }\mathit{م}\mathbf{ } \end{gathered}$$

 

                                       تمارين و مسائل   صفحة  $\mathbf{١٠١}$

 

     $\mathbf{١}\mathbf{)}\mathbf{ }$  أ ب قطعة مستقيمة تصل بين النقطتين  $\mathit{أ}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{٠}\mathbf{ }\mathbf{)}\mathbf{ }\mathit{و}\mathbf{ }\mathit{ب}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٥}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{)}\mathbf{ }$  كما هو موضح في الشكل  $\left(\mathrm{٧}-\mathrm{٥٣}\right)$  . جد 

                   أ ) طول القطعة المستقيمة أ ب 

                  ب)   قياس الزاوية الحادة المحصورة بين القطعة المستقيمة أ ب و محور السينات .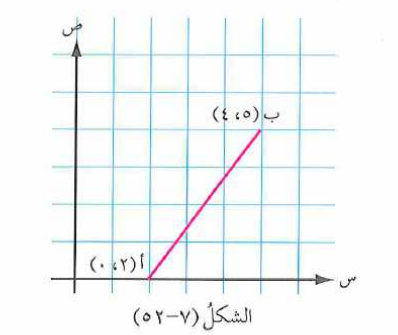                                 

 

 

                   $\mathbf{ }\mathbf{ }\mathbf{ }\mathit{أ}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{أ}\mathbf{ }\mathit{ب}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{{\left(\mathrm{٥}-\mathrm{٢}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\left(\mathrm{٤}-\mathrm{٠}\right)}^{\mathbf{٢}}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{٩}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١٦}\mathbf{ }}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٥}\mathbf{ }\mathbf{وحدات}\mathbf{ }$

 

                    ب)     أنزل عمود من النقطة ب على محور السينات عند النقطة ج فتكون  $\mathit{ج}\mathbf{ }\mathbf{(}\mathbf{ }\mathbf{٥}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{٠}\mathbf{ }\mathbf{)}\mathbf{ }$  ويكون طول العمود 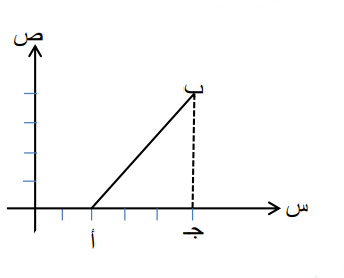 $\mathbf{ }\mathit{ب}\mathbf{ }\mathit{ج}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{وحدات}\mathbf{ }$      

 

                                الزاوية الحادة المحصورة بين القطعة المستقيمة أ ب و محور السينات  هي الزاوية أ 

 

                                 $\mathbf{جا}\mathbf{ }\mathit{أ}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{ب}\mathbf{ }\mathbf{ج}\mathbf{ }}{\mathbf{أ}\mathbf{ }\mathbf{ب}}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{٤}}{\mathbf{٨}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٨}\mathbf{,}\mathbf{٠}\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathit{أ}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١}\mathbf{,}\mathbf{٥٣}\mathbf{°}$

 

 

        $\mathbf{٢}\mathbf{)}$    يسير رجل مقتربًا من قاعدة عمود كهرباء يعلوه مصباح ارتفاعه $\left(\mathrm{٥}\right)$ م ، و في اللحظة التي كان فيها طول ظل الرجل يساوي $\left(\mathrm{٢}\right)$ م ، كان قياس الزاوية المحصورة بين المصباح

                 و رأس ظل الرجل $\mathbf{٣٨}\mathbf{°}$ . جد المسافة بين الرجل و قاعدة العمود في تلك اللحظة . 

 

                                                    $$\begin{gathered} \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ظا}\mathbf{ }\mathbf{٣٨}\mathbf{°}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{أ}\mathbf{ }\mathbf{ب}\mathbf{ }}{\mathbf{ب}\mathbf{ }\mathbf{ج}\mathbf{ }} \\ \mathbf{ }\mathbf{ }\mathbf{٧٨١٣}\mathbf{,}\mathbf{٠}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{أ}\mathbf{ }\mathbf{ب}\mathbf{ }}{\mathbf{٥}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{ }\mathit{أ}\mathbf{ }\mathit{ب}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩}\mathbf{,}\mathbf{٣}\mathbf{ }\mathit{م}\mathbf{ } \\ \mathbf{المسافة}\mathbf{ }\mathbf{بين}\mathbf{ }\mathbf{الرجل}\mathbf{ }\mathit{و}\mathbf{ }\mathbf{قاعدة}\mathbf{ }\mathbf{العمود}\mathbf{ }\mathbf{في}\mathbf{ }\mathbf{تلك}\mathbf{ }\mathbf{اللحظة}\mathbf{ }\mathbf{تساوي}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{٩}\mathbf{,}\mathbf{٣}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩}\mathbf{,}\mathbf{١}\mathbf{ }\mathit{م} \end{gathered}$$

 

 

         $\mathbf{٣}\mathbf{)}$  حل المثلث القائم الزاوية في كل من الحالات الاتية : 

 

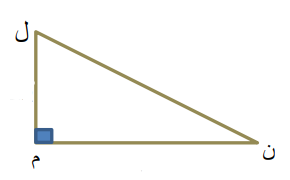
              أ )  ل م ن مثلث قائم الزاوية في م  ،  فيه  :  $\mathit{م}\mathbf{ }\mathit{ن}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{سم}\mathbf{ }\mathbf{،}\mathbf{ }\mathit{ل}\mathbf{ }\mathit{م}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{سم}\mathbf{ }$

 

                        $$\begin{gathered} \mathbf{بتطبيق}\mathbf{ }\mathbf{مبرهنة}\mathbf{ }\mathbf{فيثاغورس}\mathbf{ }\mathbf{نجد}\mathbf{ } \\ \mathbf{ }{\mathbf{(}\mathbf{ }\mathit{ل}\mathbf{ }\mathit{ن}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{٤}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١٦}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٢٠} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathit{ل}\mathbf{ }\mathit{ن}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{٢٠}\mathbf{ }}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ظا}\mathbf{ }\mathit{ل}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\frac{\mathbf{ن}\mathbf{ }\mathbf{م}\mathbf{ }}{\mathbf{ }\mathbf{ل}\mathbf{ }\mathbf{م}\mathbf{ }}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{٤}}{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٢}\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{\angle }\mathbf{ }\mathit{ل}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٤}\mathbf{,}\mathbf{٦٣}\mathbf{°} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\angle }\mathbf{ }\mathit{ن}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩٠}\mathbf{°}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٤}\mathbf{,}\mathbf{٦٣}\mathbf{°}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{\angle }\mathbf{ }\mathit{ن}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٦}\mathbf{,}\mathbf{٢٦} \end{gathered}$$

 

 

         ب)     س ص ع مثلث قائم الزاوية في ص ، فيه  $\mathbf{ }\mathit{س}\mathbf{ }\mathit{ص}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣}\mathbf{ }\mathbf{سم}\mathbf{ }$ ، وقياس الزاوية ( س ) يساوي $\mathbf{٦٠}\mathbf{°}$  ؟

                                                         

                          $$\begin{gathered} \mathbf{\angle }\mathbf{ }\mathit{ع}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩٠}\mathbf{°}\mathbf{-}\mathbf{ }\mathbf{٦٠}\mathbf{°}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣٠}\mathbf{°} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{جتا}\mathbf{ }\mathbf{٦٠}\mathbf{°}\mathbf{=}\mathbf{ }\frac{\mathbf{٣}}{\mathbf{ع}\mathbf{ }\mathbf{س}\mathbf{ }} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{٥}\mathbf{,}\mathbf{٠}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\frac{\mathbf{٣}}{\mathbf{ع}\mathbf{ }\mathbf{س}\mathbf{ }}\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathit{ع}\mathbf{ }\mathit{س}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٦}\mathbf{ }\mathbf{سم}\mathbf{ } \\ \mathbf{ }\mathbf{بتطبيق}\mathbf{ }\mathbf{مبرهنة}\mathbf{ }\mathbf{فيثاغورس}\mathbf{ }\mathbf{نجد}\mathbf{ }\mathbf{ }\mathit{ص}\mathbf{ }\mathit{ع}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{٦}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }{\left(\mathrm{٣}\right)}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{ص}\mathbf{ }\mathit{ع}\mathbf{ }\mathbf{)}}^{\mathbf{٢}\mathbf{ }\mathbf{ }}\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{ص}\mathbf{ }\mathit{ع}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣٦}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٩}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{\hspace{0.17em}}\mathit{ص}\mathbf{ }\mathit{ع}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٢٧}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{ }\mathit{ص}\mathbf{ }\mathit{ع}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{٢٧}}\mathbf{ }\mathbf{ } \end{gathered}$$

 

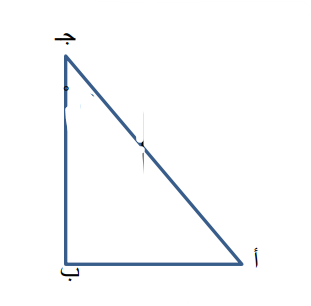
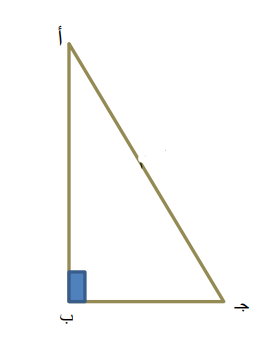
        ج)  أ ب ج مثلث قائم الزاوية في ب ، فيه :   $\mathbf{جا}\mathbf{ }\mathit{ج}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٥}\mathbf{,}\mathbf{٠}\mathbf{ }\mathbf{،}\mathbf{ }\mathbf{أج}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٤}\mathbf{ }$.

 

             $$\begin{gathered} \mathbf{ }\mathbf{جا}\mathbf{ }\mathit{ج}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٥}\mathbf{,}\mathbf{٠}\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathbf{\angle }\mathbf{ }\mathit{ج}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٣٠}\mathbf{°} \\ \mathbf{ }\mathbf{ }\mathbf{\angle }\mathbf{ }\mathit{أ}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩٠}\mathbf{°}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٣٠}\mathbf{°}\mathbf{ }\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{٦٠}\mathbf{°} \\ \mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{جا}\mathbf{ }\mathit{ج}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{أ}\mathbf{ }\mathbf{ب}\mathbf{ }}{\mathbf{١٤}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{٥}\mathbf{,}\mathbf{٠}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{أ}\mathbf{ }\mathbf{ب}\mathbf{ }}{\mathbf{١٤}}\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathit{أ}\mathbf{ }\mathit{ب}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٧}\mathbf{ }\mathbf{سم}\mathbf{ } \\ \mathbf{بتطبيق}\mathbf{ }\mathbf{مبرهنة}\mathbf{ }\mathbf{فيثاغورس}\mathbf{ }\mathbf{نجد}\mathbf{ }\mathbf{ }\mathit{ب}\mathbf{ }\mathit{ج}\mathbf{ } \\ \mathbf{ }\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{ب}\mathbf{ }\mathit{ج}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{١٤}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{-}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{٧}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{١٩٦}\mathbf{ }\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٤٩}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١٤٧} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{ب}\mathbf{ }\mathit{ج}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{١٤٧}} \end{gathered}$$

 

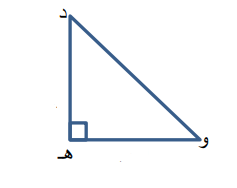
        د)   د هـ و مثلث متطابق الضلعين و قائم الزاوية في هـ ،  $\mathit{د}\mathbf{ }\mathbf{هـ}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{سم}\mathbf{ }$ 

                       $$\begin{gathered} \mathbf{ظا}\mathbf{ }\mathit{د}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{١}}{\mathbf{١}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{\leftarrow }\mathbf{ }\mathit{د}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٤٥}\mathbf{°} \\ \mathbf{\angle }\mathbf{ }\mathbf{هـ}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٩٠}\mathbf{°}\mathbf{ }\mathbf{-}\mathbf{ }\mathbf{٤٥}\mathbf{°}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{٤٥}\mathbf{°} \\ \mathbf{ }\mathbf{بتطبيق}\mathbf{ }\mathbf{مبرهنة}\mathbf{ }\mathbf{فيثاغورس}\mathbf{ }\mathbf{نجد}\mathbf{ }\mathbf{ }\mathit{د}\mathbf{ }\mathit{و}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }{\mathbf{(}\mathbf{ }\mathit{د}\mathbf{ }\mathit{و}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{ }\mathbf{+}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{)}}^{\mathbf{٢}}\mathbf{}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{١}\mathbf{ }\mathbf{+}\mathbf{ }\mathbf{١}\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{٢} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{د}\mathbf{ }\mathit{و}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{ }\mathbf{ }\sqrt{\mathbf{٢}} \end{gathered}$$