حل مسائل ثلاثية الأبعاد .

تشتمل المسائل ثلاثية الأبعاد (في الفضاء) على ثلاثة مستويات؛أفقي،وراسي،ومائل.ويتطلب حل هذه المسائل رسم مخطط يوضح الحالة،ويمثل المعلومات المعطاة فيها،ثم البحث عن مثلثات قائمة الزاوية فيها.وإذا لم توجد هذه المثلثات،فإننا نرسم بعضها،بحيث تكون بعض عناصرها معلومة،فضلا عن تحديد العنصر المطلوب إيجاده فيها؛على أن نرسم كلا منها بمنأى عن المخطط المذكور آنفا،   ليسهل علينا معرفة العلاقة التي نستخدمها في الحل

مثال

يمثل الشكل المجاور متوازي مستطيلات.أجد قياس الزاوية $AHF$،مقربا إجابتي إلى أقرب منزلة عشرية واحدة

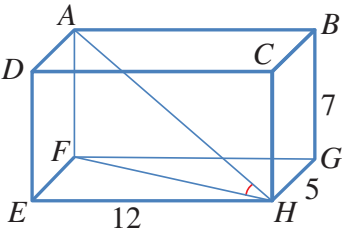
المثلث $AFH$ قائم الزاوية في $F$،ومعلوم فيه طول $AF$؛لذا يجب معرفة عنصر آخر لإيجاد القياس المطلوب 

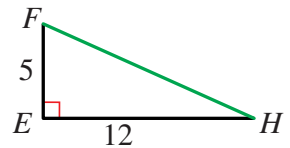
الخطوة 1:إيجاد طول $FH$ من المثلث قائم الزاوية $FEH$؛المرسوم وحده جانبا

$$\begin{gathered} {\left(FH\right)}^2={\left(EF\right)}^2+{\left(EH\right)}^2 \\ =5^2+{12}^2 \\ {\left(FH\right)}^2=169 \\ FH=\sqrt{169}=13 \end{gathered}$$

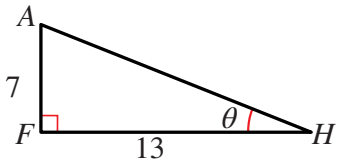
الخطوة 2:رسم المثلث $AFH$ وحدة،ثم استعمال الظل $\left(\tan \right)$ لإيجاد قياس الزاوية $AHF$

$$\begin{gathered} \tan \theta =\frac{7}{13}=0.5385 \\ \theta ={\tan }^{-1}\left(0.5385\right)=28.3° \end{gathered}$$

يمكن نمذجة كثير من المواقف الحياتية باستعمال المثلثات،ثم  إيجاد قياسات مجهولة فيها باستعمال النسب المثلثية

مثال:من الحياة 

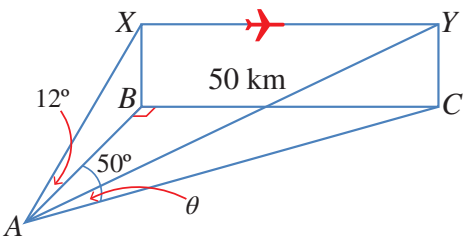
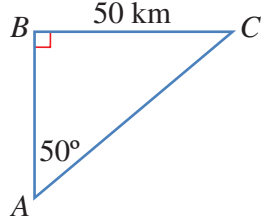
تقع النقاط $Cو،Bو،A$ في مستوى أفقي واحد على الأرض،وتقع النقطة $C$ على بعد $50km$ شرقي النقطة $B$ التي تقع شمالي النقطة $A$،وتقع النقطة $C$ في اتجاه $050°$من النقطة $A$.رصدت من النقطة $A$ حركة طائرة في موقعين مختلفين على الارتفاع نفسه عن الأرض؛الأول:عندما كانت فوق النقطة $B$ مباشرة،وكانت زاوية ارتفاعها $12°$.والثاني:عندما كانت فوق النقطة $C$.أجد زاوية ارتفاع الطائرة عندما كانت فوق النقطة $C$

الخطوة 1:ارسم مخططا يمثل المعلومات المعطاة

الخطوة 2:ارسم المثلث قائم الزاوية $ABC$،ثم استخدمه في إيجاد $ACو،AB$

الخطوة 3:ارسم المثلث قائم الزاوية $ABX$،ثم استخدمه في إيجاد $BX$،ومنه يمكن إيجاد $CY$،فهما متساويان؛لأن الشكل $BXYC$ مستطيل 

$$\begin{gathered} \tan 12°=\frac{BX}{41.95} \\ BX=41.95 \tan 12°=8.917km \end{gathered}$$

الخطوة 4:استعمل المثلث قائم الزاوية $ACY$ لإيجاد زاوية الارتفاع $\theta$

$$\begin{gathered} \tan \theta =\frac{8.917}{65.27}=0.1366 \\ \theta ={\tan }^{-1}0.1366=7.8° \end{gathered}$$

إذن،زاوية ارتفاع الطائرة عندما كانت فوق النقطة $C$ هي:$7.8°$،مقربة إلى منزلة عشرية واحدة

مثال:من الحياة

رصد المنزل $A$ في اتجاه الشرق من قمة برج يرتفع $80m$،وكذلك المنزل $B$ في اتجاه الجنوب.إذا كانت زاوية انخفاض المنزل $A$ من قمة البرج $37°$،وزاوية انخفاض المنزل $B$ من قمته $25°$،فما المسافة بين المنزلين؟

الخطوة 1:ارسم مخططا،علما بأن البرج $DC$ يصنع زاوية قائمة مع الأرض،وأن اتجاه كل من الرق والجنوب يصنعان معا زاوية معا زاوية قائمة 

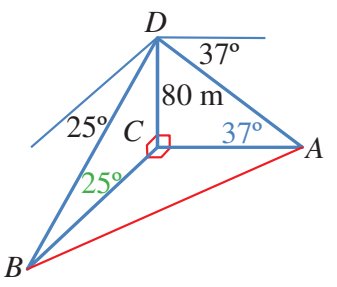
بما أن زاوية انخفاض المنزل $A$ هي $37°$،فإن الزاوية $DAC$هي $37°$،فإن الزاوية $DAC$ هي $37°$،وبما أن زاوية انخفاض المنزل $B$ هي $25°$،فإن الزاوية $DBC$ هي $25°$

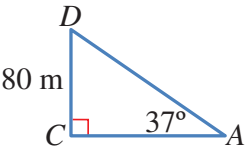
الخطوة 2:استعمل المثلث قائم الزاوية $ABC$ لإيجاد $AB$،وهذا يحتم معرفة $BCو،AC$

الخطوة 3:ارسم المثلث $ADC$ .ولإيجاد $AC$،استعمل ظل الزاوية $37°$

$$\begin{gathered} \tan 37°=\frac{80}{AC} \\ AC=\frac{80}{\tan 37°} \\ AC=106.2m \end{gathered}$$

الخطوة 4:ارسم المثلث $BCD$ .ولإيجاد $BC$،استعمل ظل الزاوية $25°$

$$\begin{gathered} \tan 25°=\frac{80}{BC} \\ BC=\frac{80}{\tan 25°} \\ BC=171.6m \end{gathered}$$

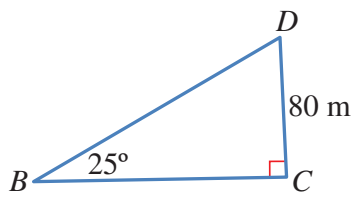
الخطوة 5:استعمل نظرية فيثاغورس في المثلث $ABC$ لإيجاد $AB$

$$\begin{gathered} {\left(AB\right)}^2={\left(AC\right)}^2+{\left(BC\right)}^2 \\ ={\left(106.2\right)}^2+{\left(171.6\right)}^2=40725 \\ AB=\sqrt{40725}=201.8 \end{gathered}$$

إذا،المسافة بين المنزلين هي:$201.8m$،مقربة إلى أقرب منزلة عشرية واحدة