حل مسائل ثلاثية الأبعاد . - حل اسئلة الدرس - الصف العاشر - رياضيات فصل أول - مدرسة جواكاديمي

أتحقق من فهمي صفحة 137

أجد $B E$ ،وقياس الزاوية $E B G$ في المثال السابق

مثال 1

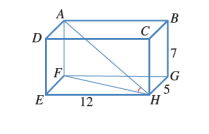
يمثل الشكل المجاور متوازي مستطيلات . أجد قياس الزاوية AHFمقربًا إجابتي إلى أقرب منزلة عشرية واحدة .

الحل :

$F H = 13 إن المثال حل حسب m A H F = 28.3 E G = F H = 13 B E^{2} = E G^{2} + B G^{2} B E^{2} = 13^{2} + 7^{2} = 169 + 49 = 218 B E = \sqrt{218} = 14.76 t a n E B H = \frac{E G}{B G} = \frac{13}{7} E B H = t a n^{- 1} (\frac{13}{7}) = 61.7$

أتحقق من فهمي صفحة 138

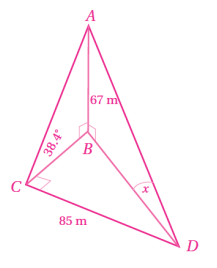
رصد أحمد قمة مئذنة من نقطة على الأرض تقع جنوب المئذنة،فكانت زاوية ارتفاعها $38.4 °$ ،ثم سار شرقا مسافة $85 m$ ،ورصد قمة المئذنة مرة أخرى.إذا كان ارتفاع المئذنة $67 m$ ،أجد زاوية ارتفاع قمة المئذنة في المرة الثانية

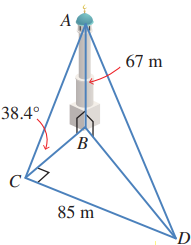
الحل :

$C B = \frac{67}{t a n 38.4} = 84.5 m B D = \sqrt{85^{2} + 84 . 5^{2}} = 119.9 m فإن ، x هي D النقطة من المئذنة قمة ارتفاع زاوية لتكن t a n x = \frac{67}{119.9} = 0.559 x = t a n^{- 1} (0.559) = 29.21$

أتحقق من فهمي صفحة 139

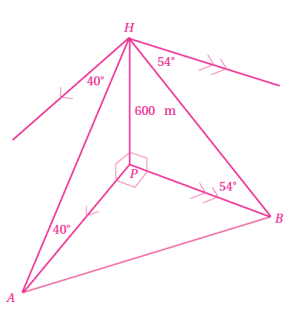
أبحرت السفينتان $B و A$ من الميناء $P$ في اتجاهين متعامدين. وقد رصدت طائرة عمودية تحلق فوق الميناء هاتين السفينتين في اللحظة نفسها،فكانت زاوية انخفاض السفينة $A$ هي $40 °$ ،وزاوية انخفاض السفينة $B$ هي $54 °$ .إذا كان ارتفاع الطائرة عن البحر $600 m$ ،فما المسافة بين السفينتين لحظة رصدهما؟

الحل :

$: أن يتبين ، H P A المثلث من A P = \frac{600}{t a n 40} = 715.1 : أن يتبين ، H P B المثلث من و B P = \frac{600}{t a n 54} = 435.9 {(A B)}^{2} = {(715.1)}^{2} + {(435.9)}^{2} = 701376.82 A B \approx 837.5 m تقريبا 837.5 m السفينتين بين المسافة إذا$

أتدرب وأحل المسائل صفحة 140

1) سارية العلم: نصبت سارية علم عموديا عند ركن ساحة مستطيلة الشكل $A B C D$ .أجد زاوية ارتفاع قمة السارية $P$ من النقطة $C$

${(AC)}^{2} = 10^{2} + 8^{2} = 164 A C = \sqrt{164} = 12.8 x هي الزاوية لتكن t a n A P C = \frac{12.8}{6} = 2.13 A P C = t a n^{- 1} 2.13 = 64.9 بالتالي x = 90 - 64.9 = 25.1$

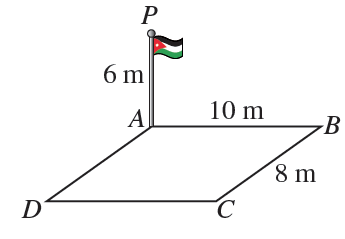
يمثل الشكل المجاور هرما قائما قاعدته $A B C D$ مستطيلة الشكل،بعداها: $15 c m و ، 20 c m$ .إذا كان طول كل من الأحرف الواصلة بين قمة الهرم ورؤوس القاعدة $24 c m$ ،وكانت القمة $V$ تقع راسيا فوق مركز القاعدة المستطيلة،فأجد:

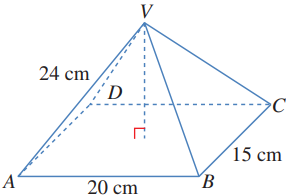
2) طول القطر $A C$

3) قياس الزاوية $V A C$

4) ارتفاع الهرم

$2) {(A C)}^{2} = 20^{2} + 15^{2} = 625 A C = \sqrt{625} = 25 3) x هي الزاوية لتكن c o s x = \frac{12.5}{24} = 0.52 x = c o s^{- 1} 0.52 = 58.7 4) y هو الهرم ارتفاع ليكن t a n x = \frac{y}{12.5} \Rightarrow t a n 58.7 = \frac{y}{12.5} 1.64 = \frac{y}{12.5} y = 1.64 \times 12.5 = 20.5$

5) منارة: شاهد صياد منارة على حافة صخرية بزاوية ارتفاع قياسها $34 °$ .إذا كان ارتفاع قاعدة المنارة عن مستوى عيني الصياد $150 m$ ،فكم يبعد الصياد عن هذه القاعدة؟

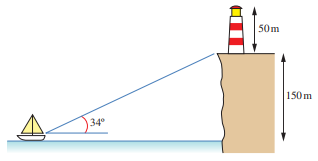
6) إذا كان ارتفاع المنارة $50 m$ ،فما زاوية ارتفاع نظر الصياد نحو قمة المنارة؟

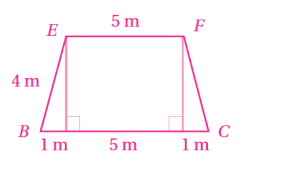
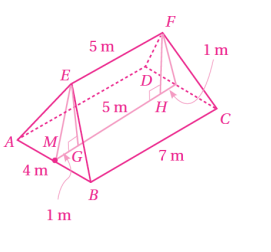
$5) t a n 34 = \frac{150}{x} x = \frac{150}{t a n 34} = 222.4 6) t a n y = \frac{150 + 50}{222.4} = \frac{200}{222.4} = 0.899 y = t a n^{- 1} 0.899 = 41.96$

يمثل الشكل المجاور سقف بناية،قاعدته الأفقي $A B C D$ الذي بعداه: $4 m و ، 7 m$ .وتمثل نهايتا السقف مثلثين متطابقي الأضلاع،في حين يمثل كل من جانبي السقف شبه منحرف متطابق الساقين.إذا كان طول الحافة العلوية $E F$ هو $5 m$ ،فأجد:

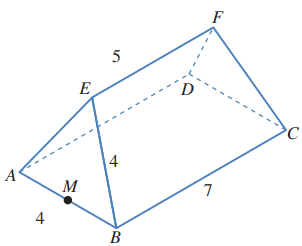
7) طول $E M$ ،حيث $M$ نقطة منتصف $A B$

8) قياس الزاوية $E B C$

9) قياس الزاوية بين $E M$ والقاعدة $A B C D$

$7) t a n E B A = \frac{EM}{2} \Rightarrow t a n 60 = \frac{EM}{2} \Rightarrow 1.75 = \frac{EM}{2} \Rightarrow E M = 3.5 8) E B C الزاوية قياس c o s^{- 1} (\frac{1}{4}) = 75.5$

الزاوية بين EM والقاعدة ABCD هي الزاوية EMG ، وإذا أنزل عمود من F إلى القاعدة تكون المستطيل EGHF ومثلثان ، وطول ثاعدة كل منهما 1m

إذا جيب تمام الزاوية EMG هو

$\frac{M G}{E M} = \frac{1}{3.46}$

وقياسها هو

$c o s^{- 1} (\frac{1}{3.46}) = 73.2$

$A B C D$ مستطيل راسي، $E D C و$ مثلث أفقي.إذا كان قياس الزاوية $C D E$ هو $90^{°}$ $E D = 9 c m و ، B C = 4 c m و ، A B = 10 c m$ ،فأجد:

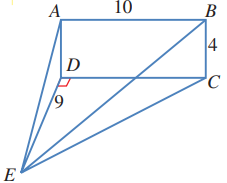
10) قياس الزاوية $A E D$

11) قياس الزاوية $D E C$

12) طول $E C$

13) قياس الزاوية $B E C$

$10) t a n A E D = \frac{4}{9} \Rightarrow A E D = t a n^{- 1} \frac{4}{9} = 24 11) t a n D E C = \frac{10}{9} \Rightarrow D E C = t a n^{- 1} \frac{10}{9} = 48 12) {(E C)}^{2} = 10^{2} + 9^{2} = 181 A C = \sqrt{181} = 13.5 13) t a n B E C = \frac{4}{13.5} \Rightarrow B E C = t a n^{- 1} \frac{4}{13.5} = 16.5$

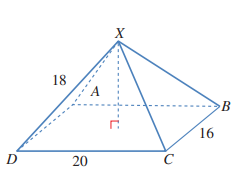
14) يمثل الشكل المجاور الهرم $X A B C D$ الذي له قاعدة مستطيلة الشكل.أجد قياس الزاوية بين الحافة $X D$ وقطر القاعدة $D B$

${(D B)}^{2} = 20^{2} + 16^{2} = 656 D B = \sqrt{656} = 25.6 c o s x = \frac{12.8}{18} = 0.71 x = c o s^{- 1} 0.71 = 44.7$

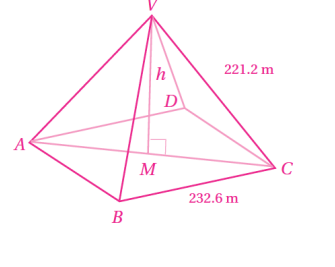
15) أحل المسألة الواردة في بداية الدرس

شيد الهرم الأكبر في مدينة الجيزة بمصر عام 2500 قبل الميلاد تقريبًا، وتمثل قاعدته مربعا طول ضلعه 232.6m وطول الضلع الواصل بين قمة الهرم وأي من رؤوس المربع 221.2m أجد ارتفاع هذا الهرم .

${(A C)}^{2} = 232 . 6^{2} + 232 . 6^{2} = 2 \times {(232.6)}^{2} A C = 232.6 \times \sqrt{2}$

النقطة M هي منتصف AC ; أي أن :

$A M = \frac{1}{2} (232.6 \times \sqrt{2}) = 116.3 \sqrt{2} h^{2} = 221 . 2^{2} - {(116.3 \sqrt{2})}^{2} = 21878.06 h = 147.9 m$

مهارات التفكير العليا

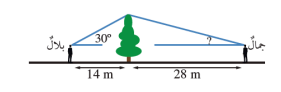
16) اكتشف الخطأ:يقف بلال على بعد $14 m$ شرقي شجرة،زاوية ارتفاع قمتها بالنسبة إليه $30 °$ ،ويقف جمال على بعد $28 m$ غربي الشجرة،وهو يرى أن زاوية ارتفاع قمة الشجرة بالنسبة إليه يجب أن تكون $15 °$ ؛لأنه يبعد عن الشجرة مثلي المسافة التي يبعدها بلال.هل رأي جمال صحيح؟إذا لم يكن رأيا صحيحا،فما زاوية الارتفاع؟

ليس صحيحًا لأن

$t a n 15 \neq \frac{1}{2} t a n 30$

ارتفاع الشجرة فوق مستوى عيني بلال هو 30 14tan إذا كانت زاوية ارتفاع الشجرة بالنسبة

إلى جمال هي $θ$ فإن :

$t a n θ = \frac{14 t a n 30}{28} = \frac{8.083}{28} θ = t a n^{- 1} (\frac{8.083}{28}) = 16.1$

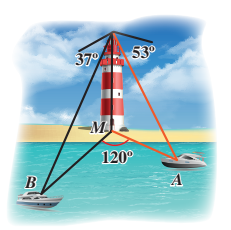
17) تحد: رصد القاربان $B و A$ في البحر من قمة منارة على الشاطئ،ارتفاعها $44 m$ ،في اللحظة نفسها،فكانت زاوية انخفاض القارب $A$ هي $53 °$ ،وزاوية انخفاض القارب $B$ هي $37 °$ ،وقياس الزاوية $A M B$ هو $120 °$ ،حيث $M$ قاعدة المنارة.أجد المسافة بين القاربين

$M B = 44 \div t a n 37 = 58.39 A M = 44 \div t a n 53 = 33.16 {(A B)}^{2} = {(58.39)}^{2} + {(33.15)}^{2} - 2 \times 58.39 \times 33.16 \times c o s 120 = 6445.1901 A B \approx 80.3 m$

كتاب التمارين

أتأمل الشكل المجاور،ثم أحل المسألتين الآتيتين:

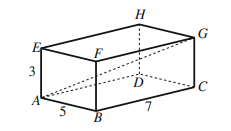
1) أجد طول القطر $A G$ في متوازي المستطيلات المجاور

$A C = \sqrt{5^{2} + 7^{2}} = \sqrt{74} A G = \sqrt{74 + 3^{2}} = \sqrt{83} \approx 9.1$

2) أجد قياس الزاوية $G A C$

$m ∠ G A C = t a n^{- 1} (\frac{3}{\sqrt{74}}) \approx 19.2 °$

أتأمل الشكل المجاور،ثم أحل المسألتين الآتيتين:

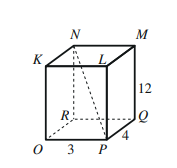
3) أجد طول القطر $N P$ في متوازي المستطيلات المجاور

$R P = \sqrt{3^{2} + 4^{2}} = 5 N P = \sqrt{5^{2} + 12^{2}} = \sqrt{169} = 13$

4) أجد قياس الزاوية $N P R$

$m ∠ N P R = t a n^{- 1} (\frac{12}{5}) \approx 67.4$

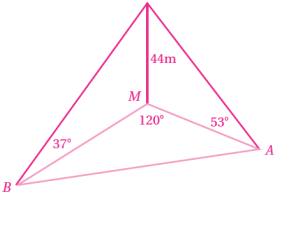
5) قياسات: رصد رجلان على الأرض من قمة برج رأسي ارتفاعه 25m ، فكانت زاوية انخفاض الرجل الأول الذي يقف غرب البرج هي $31 °$ ، وزاوية انخفاض الرجل الثاني الذي يقف جنوب البرج هي $17 °$ . ما المسافة بين الرجلين ؟

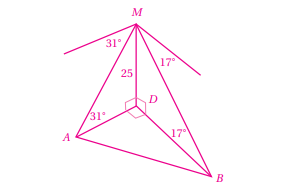
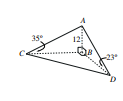
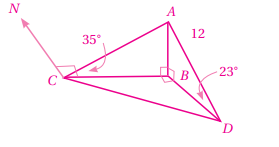
$B D = \frac{25}{t a n 17 °} \approx 81.8 A D = \frac{25}{t a n 31 °} \approx 41.6 A B = \sqrt{81 . 8^{2} + 41 . 6^{2}} = 91.8 m$

6)سارية : يبين الشكل المجاور سارية رأسية $\bar{A B}$ ارتفاعها 12m ، والنقاط : B ، و C و D الواقعة في مستوى أفقي واحد ، بحيث كانت C غرب B و D جنوب B ، وكانت زاوية ارتفاع قمة السارية من النقطة D هي $23 °$ ، ومن النقطة C هي $35 °$ : ما طول $\bar{C D}$ ؟ ما اتجاه النقطة D من النقطة C ؟

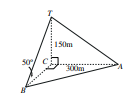
$C B = \frac{12}{t a n 35 °} \approx 17.1 m; D B = \frac{12}{t a n 23 °} \approx 28.3 m C D = \sqrt{17 . 1^{2} + 28 . 3^{2}} = 33.1 m \vec{C D} الشمال خط بين الزاوية قياس يساوي C من D اتجاه \bar{C D} والقطعة m ∠ N C B + m ∠ B C D : وهو = 90 ° + t a n^{- 1} (\frac{28.3}{17.1}) \approx 90 ° + 58.9 ° = 148.9 °$

7)أبراج : تمثل $\bar{T C}$ برج إرسال رأسي ارتفاعه 150m وهو مدعم برباطين معدنيين ، هما : $\bar{T A}$ و $\bar{T B}$ وكان أحدهما مثبتًا عند النقطة A الواقعة على الأرض شرق قاعدة البرج ، وتبعد مسافة 300m وكان الآخر مثبتًا عند النقطة B جنوب قاعدة البرج، وزاوية ميله عن الأرض $50 °$ . ما المسافة بين النقطتين A و B ؟ ما اتجاه النقطة A من النقطة B ؟

$B C = \frac{15}{t a n 50} \approx 125.9 m A B = \sqrt{125 . 9^{2} + 300^{2}} \approx 325.3 m$

اتجاه A من B يساوي قياس الزاوية CBA ؛ لأن BC هو خط الشمال المار ب B وهي $t a n^{- 1} (\frac{300}{125.9}) \approx 67.2 °$

إذا ؛ الاتجاه المطلوب هو $067.2 °$

رياضيات فصل أول

العاشر

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS