حل نظام متباينات خطية بيانيًا
فكرة الدرس : حل نظام مُكوّن من متباينات خطية بيانيًا
يتكون نظام المتباينات الخطية من متباينتين خطيّتين أو أكثر ، ويُطلق على مجموعة الأزواج المرتبة التي تُحقق جميع المتباينات اسم مجموعة الحل .
مثلًا : يتكون النظام الآتي من ثلاث متباينات :
يُمثل الزوج المُرتب أحد حلول هذا النظام ؛ لأنه يحقق المتباينات جميعها .
| الزوج المرتب يحقق المتباينة الأولى (1) | |
| الزوج المرتب يحقق المتباينة الثانية (2) | |
| الزوج المرتب يحقق المتباينة الثالثة (3) |
•• علمًا أنه يوجد عدد لا نهائي من الأزواج المرتبة التي تحقق هذا النظام وليس فقط.
لحل نظام متباينات ، أمثل كل متباينة فيه بيانيًا على المستوى الإحداثي نفسه ثم أظلل المنطقة المشتركة بين مناطق حل المتباينات جميعها التي تمثل حل النظام .
مثال :
أمثل منطقة حل نظام المتباينات الآتي ، ثم أتحقق من صحة الحل .
الحل :
الخطوة 1 : أمثل المستقيمين الحدوديين :
الخطوة 2 :تحديد منطقة التقاطع بين حليّ المتباينتين :
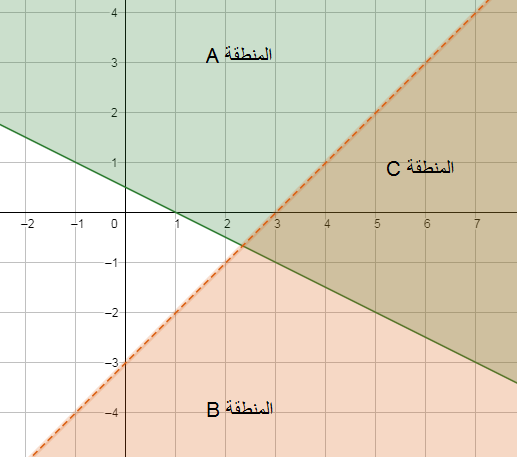
ألاحظ أنّ حل المتباينة هو المنطقتان A ، C وأنّ حل المتباينة هو المنطقتان B ، C ، إذن المنطقة C المشتركة بين منطقتي حل المتباينتين هي منطقة حل نظام المتباينات .
الخطوة 3 : أتحقق من صحة الحل :
أتحقق من صحة الحل باختيار زوج مرتب يقع في منطقة حل النظام C مثل (1 ، 5) ثم أعوضه في متباينات النظام جميعها :
| المتباينة الأولى | |
| المتباينة الثانية |
•• لا يكون لنظام المتباينات حل أحيانًا ؛ لعدم وجود منطقة مشتركة بين مناطق حل المتباينات المُكونة له ، عندئذ تكون مجموعة الحل هي المجموعة الخالية .
مثال :
أمثل منطقة حل نظام المتباينات الآتي:
|
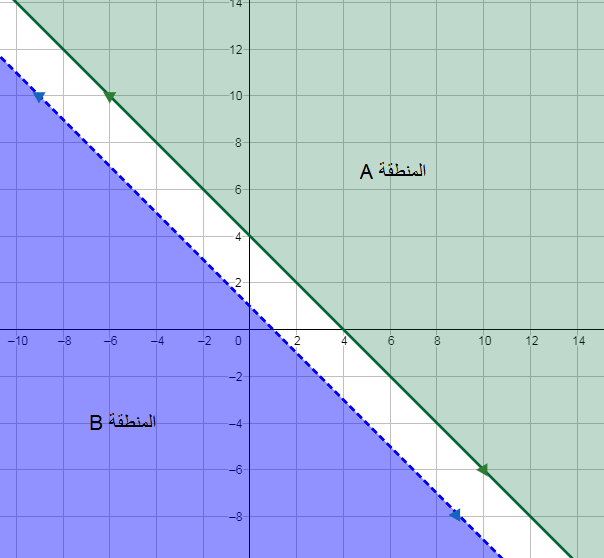
الحل : أمثل بيانيًا المستقيمين الحدوديين : على المستوى الإحداثي نفسه ، وأستخدم لونين مختلفين لتظليل منطقتي الحل ، كما في الشكل المجاور ألاحظ أنّ حل المتباينة 4 x + y هو المنطقة A ، وأنّ حل المتباينة x + y < 1 هو المنطقة B ، وأنه لا يوجد تقاطع بين منطقتي حل المتباينتين . إذن حل النظام هو المجموعة الخالية .
|
 |
•• قد يحوي النظام أكثر من متباينتين ،عندئذ تكون منطقة الحِّل هي المنطقة المشتركة بين مناطق حِّل المتباينات جميعها.
مثال :
أمثل منطقة حل نظام المتباينات الآتي:
|
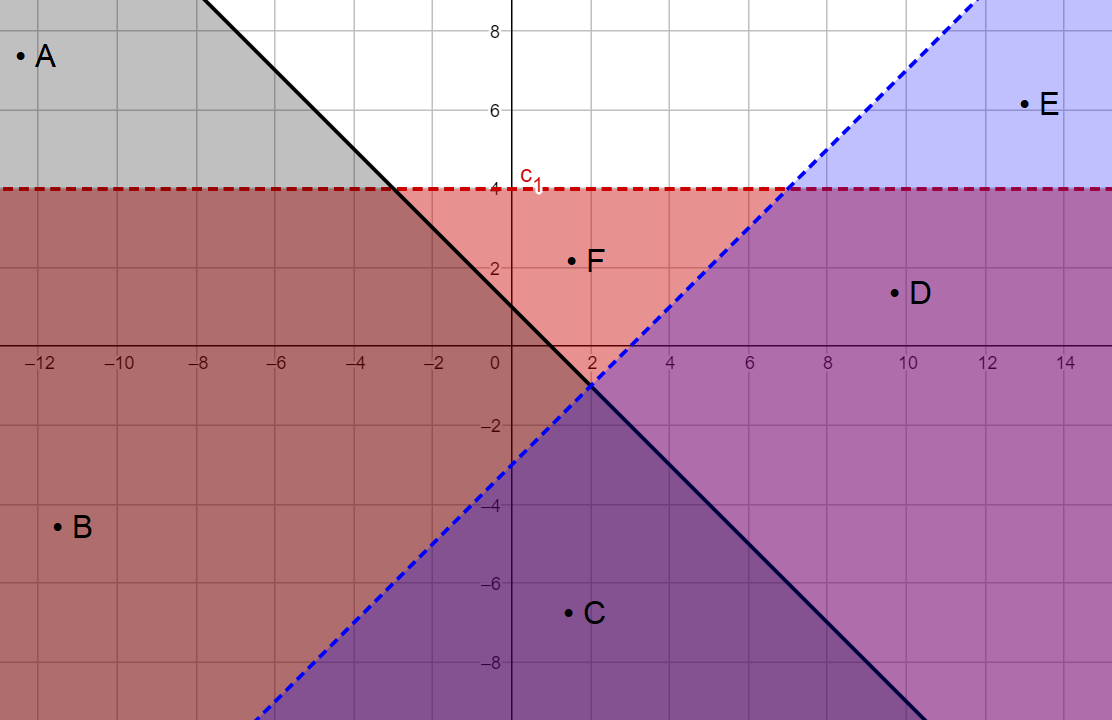
الحل : الخطوة 1 : أُمثِّل بيانيًّا المستقيمات الحدودية : على المستوى الإحداثي نفسه كما في الشكل المجاور. الخطوة 2 : تحديد منطقة الحل.
|
 |
مثال :
مع عبير 40 ديناراً ، أرادت أن تشتري بها صنفين من الشوكولاتة ، إذا كان سعر العلبة من الصنف الأول 9 دنانير ، وسعر العلبة من الصنف الثاني 4 دنانير ،
فما عدد علب الشوكولاتة من كِلا الصنفين التي ممكن أن تشتريها عبير إذا أرادت شراء 4 علب على الأقل .
الحل :
|
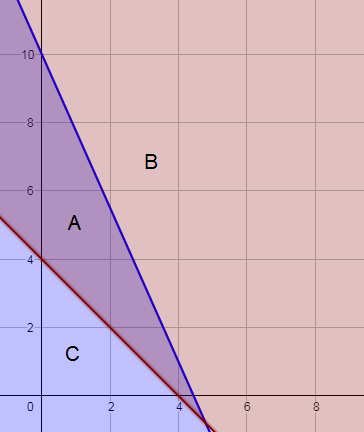
أكوّن المتباينات من معطيات السؤال : أفرض عدد علب الشوكولاتة التي ستشتريها عبير من الصنف الأول x ، وعدد علب الشوكولاتة من الصنف الثاني y متباينة عدد العلب : متباينة الثمن : أمثل المتباينات في المستوى الإحداثي نفسه : أظلل منطقة حل المتباينة ، وهي المناطق A , B أظلل منطقة حل المتباينة وهي المناطق A , C المنطقة المشتركة هي A إذن حل النظام هي المنطقة A ، ويؤخذ منها فقط الأعداد الصحيحة الموجبة ، لأن أعداد علب الشوكولاتة لا تكون إلا أعداد صحيحة موجبة . |
 |